【数III微分】平均値の定理を用いた不等式の証明の仕組み

平均値の定理って習ったけど証明が何したいのがさっぱりです。
平均値の定理って実際出されても定理使うの気づかないこと多いよね。ただそれだと難関大の問題とか解けなくなっちゃうから，一応基本からおさらいしておこうか。

平均値の定理の仕組み

まず，関数 y=f(x)y=f(x) という何らかの関数があったとします。これの接線の傾きは y’=f(x)y’=f(x) です。

次に x=ax=a のときの yy の値を y=f(a)y=f(a) として，点A (a,f(a))(a,f(a)) とします。同じように x=bx=b のときの yy の値を y=f(b)y=f(b) として，点B (b,f(b))(b,f(b)) とします。

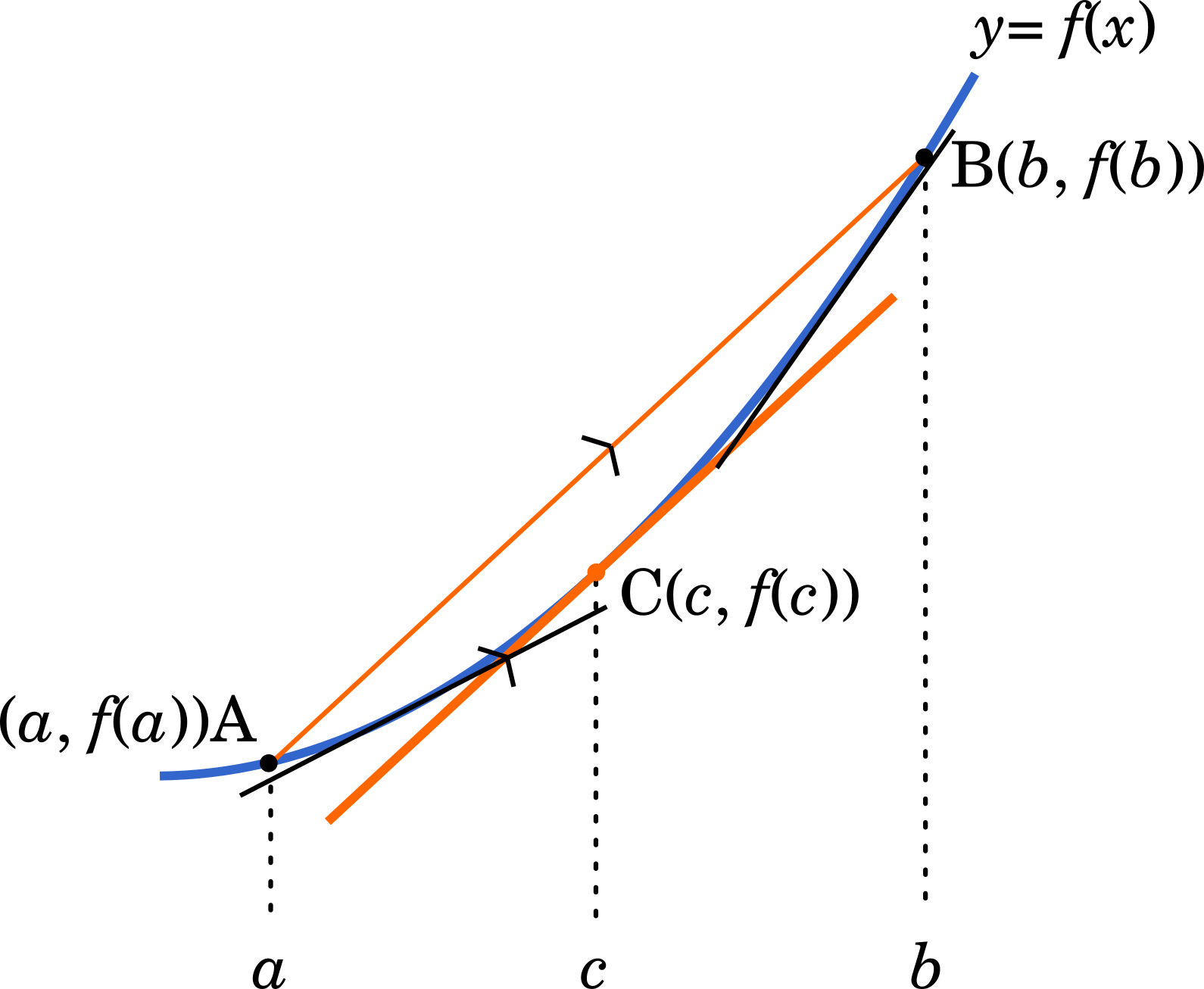
さらに，直線 AB の傾きを求めます。直線の傾きは yの変化量xの変化量\cfrac{y \text{の変化量}}{x \text{の変化量}} だから，y(b)−y(a)b−a\cfrac{y(b)-y(a)}{b-a} となります。

で？
で，このとき f(x)f(x) は区間 (a,b)(a,b) の間で色々な接線が作れるよね？　そして，その中に必ず直線 AB と同じ傾きになる接線が作れるポイント C が存在する。これが平均値の定理。
平均値の定理
f(b)−f(a)b−a=f′(c)\cfrac{f(b)-f(a)}{b-a}=f'(c)，aa ＜ cc ＜ bb を満たす実数 cc が存在する。
ただし，f(x)f(x) は区間 (a,b)(a,b) で連続していて微分可能っていう条件がある。ようするに関数に絶対値とかついていなければ使えると思っておけばよい。
グラフで言うと，接線の傾きって点 A に近いところでは直線 AB の傾きより小さくなるし，点 B に近いところでは直線 AB の傾きより大きくなってるじゃない？　だからその途中で直線 AB と同じ傾きのポイントがあるってのはグラフ見たらだいたいイメージできると思う。
これ，どう使うんですか
証明で使う。直線 AB の傾きが同じになる点 C ってのが必ず存在するけど，C の xx 座標を x=cx=c ってすると，cc は aa と bb の間にあるんだから，aa ＜ cc ＜ bb っていう不等式が成り立つよねっていう手順で証明する。つまり不等式の証明で使える。

平均値の定理と不等式の証明

[問題] 次の不等式を証明しなさい。

00 ＜ aa ＜ bb のとき，1b\cfrac{1}{b} ＜ log⁡b−log⁡ab−a\cfrac{\log b-\log a}{b-a} ＜ 1a\cfrac{1}{a}

いきなり意味不明。

まず気づかないといけないのは log⁡b−log⁡ab−a\cfrac{\log b-\log a}{b-a} の部分が yの変化量xの変化量\cfrac{y \text{の変化量}}{x \text{の変化量}} になっていることです。log⁡a\log a と log⁡b\log b が yy の値であるとするならば，y=log⁡xy=\log x という関数が考えられます。そこで，いったん f(x)=log⁡xf(x)=\log x とします。

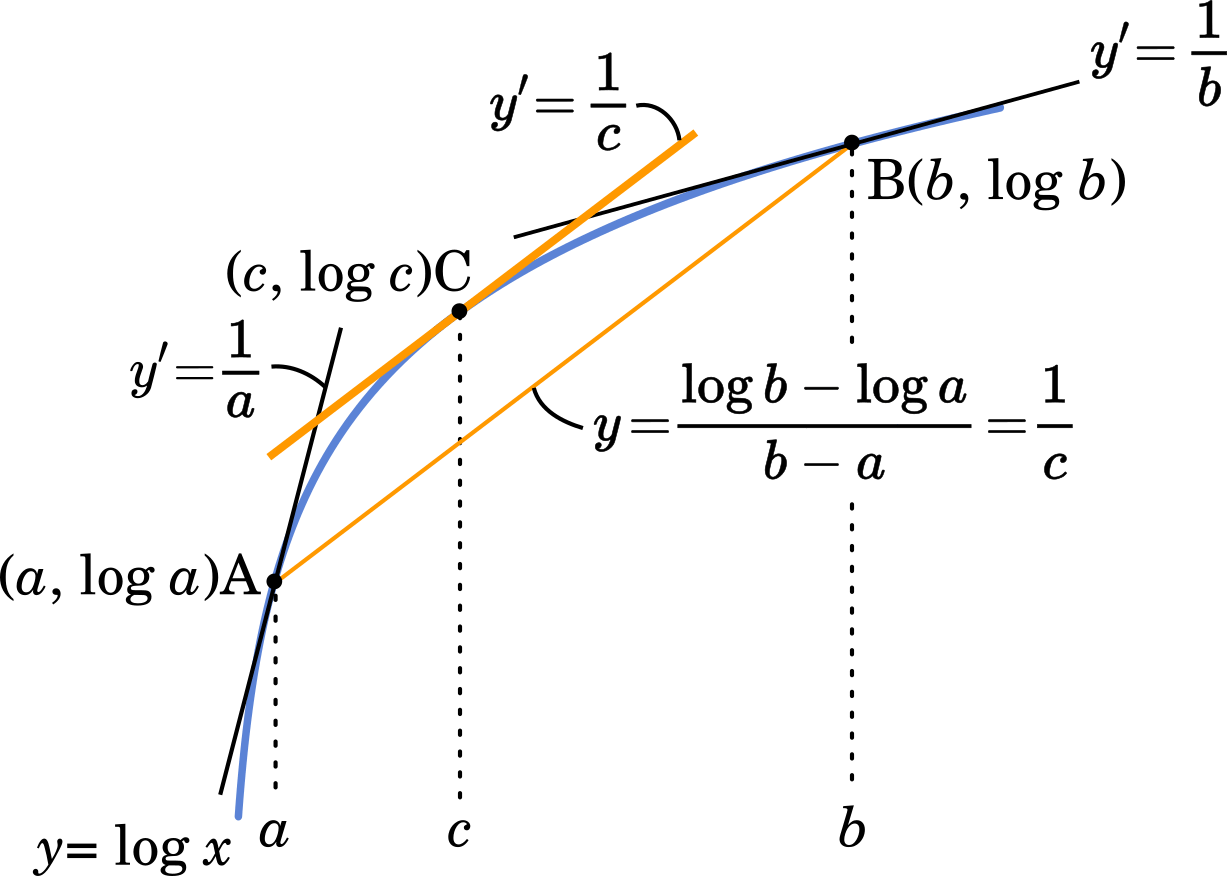
グラフをもとに考えてみましょう。関数 y=log⁡xy=\log x における接線の傾きは (log⁡x)’=1x(\log x)’=\cfrac{1}{x} となるので，xx の値が aa，bb のときの接線の傾きはそれぞれ 1a\cfrac{1}{a}，1b\cfrac{1}{b} です。

そして点 A と 点 B の間に点 C をおきます。点 C はその接線の傾き 1c\cfrac{1}{c} が直線 AB の傾きと同じになる点とします。平均値の定理より，この点は A，B の間のどこかに必ず作ることができます。

グラフを見ると分かりますが，log⁡x\log x のグラフでは xx の値が大きくなるほど接線の傾きが小さくなります。それぞれ比べると 1b\cfrac{1}{b} ＜ 1c\cfrac{1}{c} ＜ 1a\cfrac{1}{a} の関係になっています。

そして，直線 AB の傾き＝点 C の接線の傾き なので，不等式は

1b\cfrac{1}{b} ＜ log⁡b−log⁡ab−a\cfrac{\log b-\log a}{b-a} ＜ 1a\cfrac{1}{a}

となり証明終了です。

要するに式が直線 AB の傾きの形になっていれば，点 A，B の間に点 C を作って傾きどうしのイコール関係に持ち込めるよねってのがひらめいたら証明ができるという流れ。
なるほど。

[証明]

f(x)=log⁡xf(x)=\log x とすると，f(x)f(x) は区間 [aa，bb] で連続，区間 (aa，bb) で微分可能であり f′(x)=1xf'(x)=\cfrac{1}{x}

[　] と (　) はどう違うの？
[　] を閉区間って言って，端点を含む。要は aa ≦ xx ≦ bb。(　) は開区間で端点を含まない。aa ＜ xx ＜ bb ということ。説明は省くけど，微分可能って言うときには端点は含まないから (　) で表す必要がある。お約束みたいなもの。

区間[aa，bb]において，平均値の定理より

log⁡b−log⁡ab−a=1c\cfrac{\log b-\log a}{b-a}=\cfrac{1}{c} ・・・①

aa ＜ cc ＜ bb ・・・②

を満たす実数 cc が存在する。

こっちは [　] で書くんですね。
aa，bb は端点の xx 座標だから，端点を含む必要がある。

0 ＜ aa ＜ bb と②より

1b\cfrac{1}{b} ＜ 1c\cfrac{1}{c} ＜ 1a\cfrac{1}{a}

これに①を代入して

1b\cfrac{1}{b} ＜ log⁡b−log⁡ab−a\cfrac{\log b-\log a}{b-a} ＜ 1a\cfrac{1}{a} （証明終わり）

平均値の定理と極限

[問題]　lim⁡x→0e2x−12x\displaystyle\lim_{x\rightarrow0}\cfrac{e^{2x}-1}{2x} を求めよ。

平均値の定理の形に持っていくために式に手を加えましょう。1=e01=e^0 とすることができるので，

e2x−12x=e2x−e02x−0\cfrac{e^{2x}-1}{2x}=\cfrac{e^{2x}-e^0}{2x-0}

と書き換えられます。

次に，不等式を用意しましょう。ただし，不等式は xx を正の側から 0 に寄せていく場合と負の側から 0 に寄せていく場合で不等号の関係が逆になるので，場合分けしていきます。また分母が 2x2x なので，x≠0x\not=0 が前提になります。したがって，場合分けに 0 を含まないように注意しましょう。

[証明]

(i) xx ＞ 0 のとき

f(x)=exf(x)=e^x とすると，f(x)f(x) は区間 [00，2x2x] で連続，区間 (00，2x2x) で微分可能であり f′(x)=exf'(x)=e^x

区間[00，2x2x]において，平均値の定理より

e2x−e02x−0=ec\cfrac{e^{2x}-e^0}{2x-0}=e^c ・・・①

00 ＜ cc ＜ 2x2x ・・・②

を満たす実数 cc が存在する。

ここからの証明の書き方は一通りではないのだけど，今回は他でも使いまわしが効くようにはさみうちの原理でやってみる。

f(x)=exf(x)=e^x は単調増加するから，②より

e0e^0 ＜ ece^c ＜ e2xe^{2x}

e0e^0 ＜ e2x−12x\cfrac{e^{2x}-1}{2x} ＜ e2xe^{2x}

また

e0=1e^0=1 (または lim⁡x→+0e0=1\displaystyle\lim_{x\rightarrow+0}e^0=1 とも書ける)

lim⁡x→+0e2x=1\displaystyle\lim_{x\rightarrow+0}e^{2x}=1

よって，はさみうちの原理より

lim⁡x→+0e2x−12x=1\displaystyle\lim_{x\rightarrow+0}\cfrac{e^{2x}-1}{2x}=1

はさみうちの原理って何でしたっけ？

他のところで習うヤツだけど，要するに

lim⁡x→+0e0\displaystyle\lim_{x\rightarrow+0}e^0 ＜ lim⁡x→+0e2x−12x\displaystyle\lim_{x\rightarrow+0}\cfrac{e^{2x}-1}{2x} ＜ lim⁡x→+0e2x\displaystyle\lim_{x\rightarrow+0}e^{2x}

11 ＜ lim⁡x→+0e2x−12x\displaystyle\lim_{x\rightarrow+0}\cfrac{e^{2x}-1}{2x} ＜ 11

てなるから，lim⁡x→+0e2x−12x=1\displaystyle\lim_{x\rightarrow+0}\cfrac{e^{2x}-1}{2x}=1 が言えるっていう仕組み。

(ii) xx ＜ 0 のとき

f(x)=exf(x)=e^x とすると，f(x)f(x) は区間 [2x2x，00] で連続，区間 (2x2x，00) で微分可能であり f′(x)=exf'(x)=e^x

区間[00，2x2x]において，平均値の定理より

e0−e2x0−2x=ec\cfrac{e^0-e^{2x}}{0-2x}=e^c ・・・①

2x2x ＜ cc ＜ 00 ・・・②

を満たす実数 cc が存在する。

f(x)=exf(x)=e^x は単調増加するから，②より

e2xe^{2x} ＜ ece^c ＜ e0e^0

e2xe^{2x} ＜ e2x−12x\cfrac{e^{2x}-1}{2x} ＜ e0e^0

ここは e0−e2x0−2x=1−e2x−2x=e2x−12x\cfrac{e^0-e^{2x}}{0-2x}=\cfrac{1-e^{2x}}{-2x}=\cfrac{e^{2x}-1}{2x} ということ。

また

e0=1e^0=1

lim⁡x→−0e2x=1\displaystyle\lim_{x\rightarrow-0}e^{2x}=1

よって，はさみうちの原理より

lim⁡x→−0e2x−12x=1\displaystyle\lim_{x\rightarrow-0}\cfrac{e^{2x}-1}{2x}=1

したがって，(i)，(ii)より

lim⁡x→0e2x−12x=1\displaystyle\lim_{x\rightarrow0}\cfrac{e^{2x}-1}{2x}=1 (答え)

SNSでシェア

mm参考書 2019-2023