【数IIBベクトル】平面におろした垂線との交点(北海道大2019理系第1問)
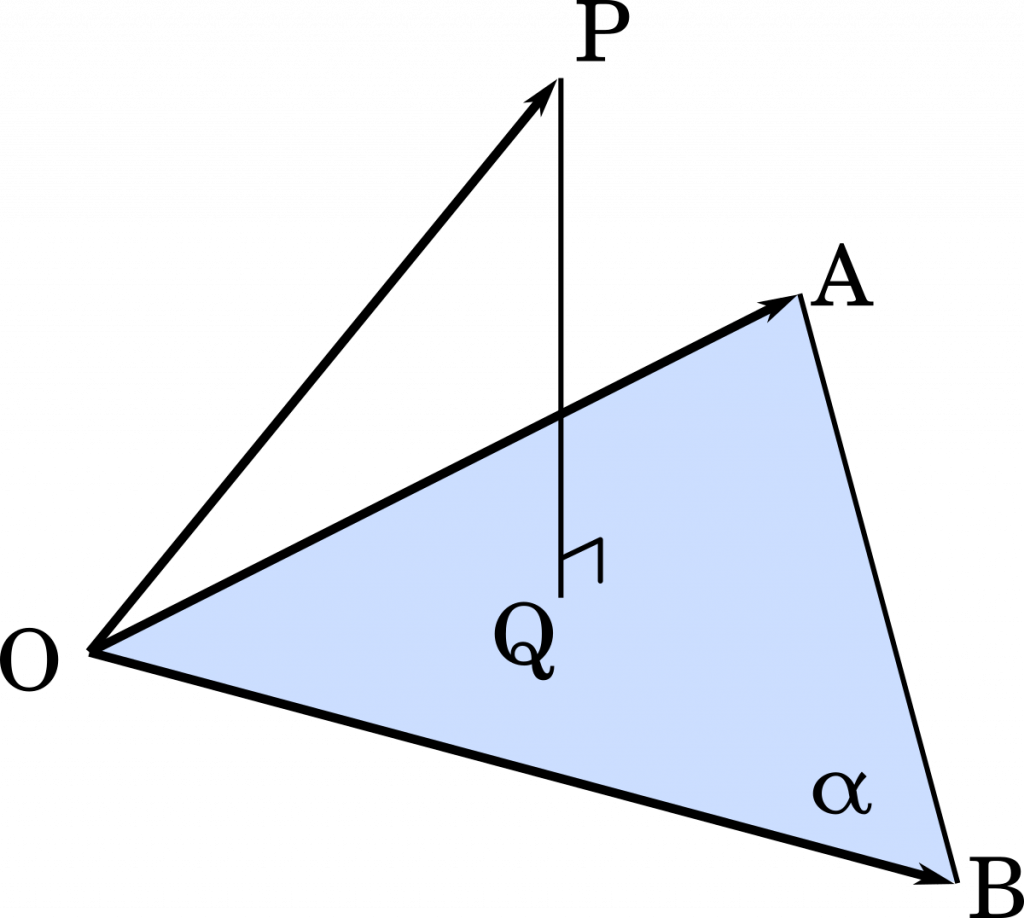
$p$ を負の実数とする。座標空間に原点 O と 3 点 A $(-1,2,0)$,B $(2,-2,1)$,P $(p,-1,2)$ があり,3 点 O,A,B が定める平面を $\alpha$ とする。また,点 P から平面 $\alpha$ に垂線を下ろし,$\alpha$ との交点を Q とする。(北海道大2019)
(1) 点 Q の座標を $p$ を用いて表せ。
(2) 点 Q が △OAB の周または内部にあるような $p$ の範囲を求めよ。
平面に垂線をおろす
(1) から始めます。
平面に垂線を下ろす問題は,やり方が決まっています。
① 平面上の点 Q を $\overrightarrow{\text{OQ}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$ のように $s,t$ を用いて表す。
② 直線 PQ と 直線 OA が垂直であることから内積 = 0 の式を作る。
③ 同様に直線 PQ と直線 OB で,内積 = 0 の式を作る。
方針は決まったので,式を作っていきましょう。
$\overrightarrow{\text{OQ}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$
$=s(-1,2,0)+t(2,-2,1)$
また,$\overrightarrow{\text{OQ}}=(x,y,z)$ とすると
$(x,y,z)=s(-1,2,0)+t(2,-1,1)$
$x=-s+2t$
$y=2s-2t$
$z=t$
となる。
ここで,成分表示のときの内積の公式を思い出しましょう。
$(x_1,y_1,z_1)$ と $(x_2,y_2,z_2)$ の内積は
$x_1x_2+y_1y_2+z_1z_2$
$\overrightarrow{\text{PQ}}=\overrightarrow{\text{OQ}}-\overrightarrow{\text{OP}}$ より
$\overrightarrow{\text{PQ}}=(-s+2t-p,2s-2t+1,t-2)$
$\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{OA}}=0$ より
$-(-s+2t-p)+2(2s-2t+1)+0\cdot(t-2)=0$
$s-2t+p+4s-4t+2=0$
$6t-5s=p+2$ ・・・①
$\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{OB}}=0$ より
$2(-s+2t-p)-2(2s-2t+1)+t-2=0$
$-2s+4t-2p-4s+4t-2+t-2=0$
$9t-6s=2p+4$ ・・・②
式を連立して
①×3 – ②×2
$18t-15s=3p+6$
$18t-12s=4p+8$
より
$-3s=-p-2$
$3s=p+2$
$s=\cfrac{p+2}{3}$
①に代入して
$6t-5\cdot\cfrac{p+2}{3}=p+2$
$18t-5p-10=3p+6$
$18t=8p+16$
$t=\cfrac{4(p+2)}{9}$
$x,y,z$ にそれぞれ代入すると
$x=-\cfrac{p+2}{3}+2\cdot\cfrac{4(p+2)}{9}$
$=\cfrac{-3p-6+8p+16}{9}$
$=\cfrac{5(p+2)}{9}$
$y=2\cdot\cfrac{p+2}{3}-2\cdot\cfrac{4(p+2)}{9}$
$=\cfrac{6p+12-8p-16}{9}$
$=-\cfrac{2(p+2)}{9}$
$z=\cfrac{4(p+2)}{9}$
したがって,点 Q の座標は
$\Big(\cfrac{5(p+2)}{9},-\cfrac{2(p+2)}{9},\cfrac{4(p+2)}{9}\Big)$
平面の内部にある点を求める
(2)に進みます。
点 Q が △OAB の周または内部にあるとき
$s+t\leqq 1$
$s\geqq0$,$t\geqq0$
が成り立ちます。



$s+t\leqq1$ より
$\cfrac{p+2}{3}+\cfrac{4(p+2)}{9}\leqq1$
$3p+6+4p+8\leqq9$
$7p\leqq-5$
$p\leqq-\cfrac{5}{7}$
また,$s\geqq0$ より
$\cfrac{p+2}{3}$
$t\geqq0$ より
$\cfrac{5(p+2)}{9}\geqq0$
$p\geqq-2$
以上より,$-2\leqq p\leqq-\cfrac{5}{7}$ (答え)
SNSでシェア