2次関数に法線を引くことができる条件を求める(東京都立大2019理学部第3問)
放物線 $y=\cfrac{1}{2}x^2$ を $C$ とする。以下の問いに答えなさい。(東京都立大2019)
(1) $C$ 上の点 $\Big(t,\cfrac{1}{2}t^2\Big)$ における接線の方程式と法線の方程式を求めなさい。
(2) 点 P$(a,b)$ から $C$ 相異なる 2 本の接線を引くことができるための,$a$ と $b$ についての条件を求めなさい。
(3) $a>0$ のとき,点 P$(a,b)$ から $C$ に相異なる 3 本の法線を引くことができるための,$a$ と $b$ についての条件を求めなさい。
接線と法線を求める
(1)から始めます。
まずは,接線の傾きを求めるために微分しましょう。
$y=\cfrac{1}{2}x^2$
$y’=x$
$x=t$ とすると,$y’=t$ だから,接線の傾きは $t$
$\Big(t,\cfrac{1}{2}t^2\Big)$ を通る傾き $t$ の直線の式は
$y-\cfrac{1}{2}t^2=t(x-t)$
$y=tx-t^2+\cfrac{1}{2}t^2$
$=tx-\cfrac{1}{2}t^2$ (答え)
次に,法線の傾きを $m$ とすると
$tm=-1$
$m=-\cfrac{1}{t}$

したがって,法線は
$y-\cfrac{1}{2}t^2=-\cfrac{1}{t}(x-t)$
$y=-\cfrac{1}{t}x+1+\cfrac{1}{2}t^2$ (答え)
接線を引くことができる条件
(2)に進みます。
(1)より接線の式は $y=tx-\cfrac{1}{2}t^2$ です。
これが $(a,b)$ を通るので,座標を代入すると
$b=at-\cfrac{1}{2}t^2$
となります。式を変形して
$2b=2at-t^2$
$t^2-2at+2b=0$


つまり,2 本の接線が引けることは,異なる 2 つの実数解が存在することと同じです。




そこで,判別式を用います。
$\dfrac{D}{4}=a^2-2b>0$
$a^2>2b$
$b<\cfrac{a^2}{2}$ (答え)
法線を引くことができる条件
(3)に進みます。
$(a,b)$ を通るので,まずは法線の式に代入していきましょう。
(1)より,法線は
$y=-\cfrac{1}{t}x+1+\cfrac{1}{2}t^2$
$(a,b)$ を通るので
$b=-\cfrac{1}{t}a+1+\cfrac{1}{2}t^2$
ここから,(2)と同じようにして,$t$ が異なる 3 つの実数解を持つ条件を考えていきます。
両辺を $2t$ 倍して
$2bt=-2a+2t+t^3$
$t^3+2t-2bt-2a=0$
ここで定数分離をしておきます。
$t^3+2(1-b)t=2a$
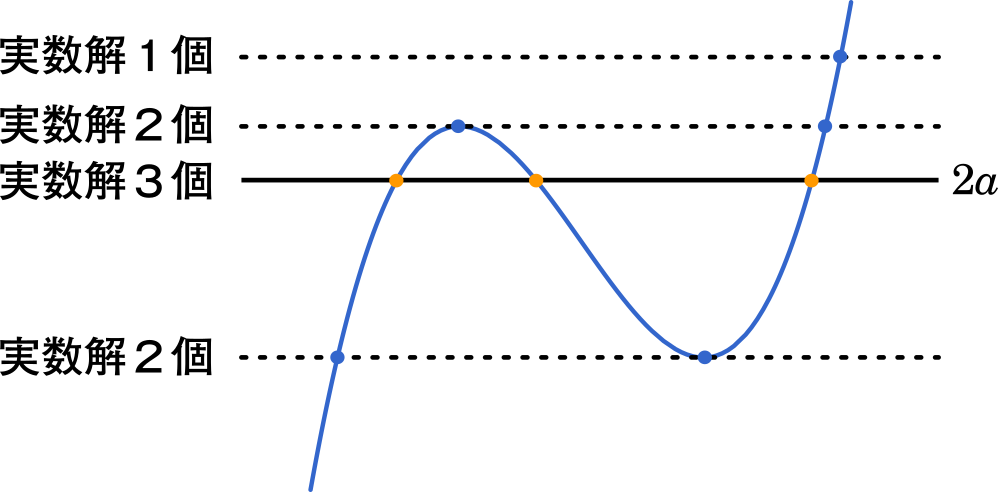
グラフを描いてみると上のようになります。縦方向で見ると,$2a$ が 2 つの極値の間にあるときに 3 つの実数解が存在するということです。
$f(t)=t^3+2(1-b)t$ として
$f'(t)=3t^2+2(1-b)$
$3t^2+2(1-b)=0$ とすると
$3t^2=-2(1-b)$
$t^2=-\cfrac{2}{3}(1-b)$
$t=\pm\sqrt{-\cfrac{2}{3}(1-b)}$
よって,$f(t)$ は $t=\pm\sqrt{-\cfrac{2}{3}(1-b)}$ で極値をとる。
このままでは計算がやっかいになるので,いったん $\sqrt{-\cfrac{2}{3}(1-b)}=\alpha$ としておきます。
これをさらに式変形して
$-\cfrac{2}{3}(1-b)=\alpha^2$
$2(1-b)=-3\alpha^2$ ・・・①
増減表は
$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline t&\cdots&-\alpha&\cdots&\alpha&\cdots\\\hline f'(t)&+&0&-&0&+\\\hline f(t)&\nearrow&&\searrow&&\nearrow\\\hline\end{array}$
$f(-\alpha)=-\alpha^3-2(1-b)\alpha$
①を代入して
$=-\alpha^3+3\alpha^3=2\alpha^3$
$f(\alpha)=\alpha^3+2(1-b)\alpha$
①を代入して
$=\alpha^3-3\alpha^2=-2\alpha^3$
よって,式が 3 つの異なる解をもつとき
$-2\alpha^3<2a<2\alpha^3$
$-\alpha^3<a<\alpha^3$
が成り立つ。
また,問題文より $a>0$ だから
$0<a<\alpha^3$
$a<\alpha^3$ について整理すると
$a^{\small{\frac{1}{3}}}<\alpha$
$a^{\small{\frac{1}{3}}}<\sqrt{-\cfrac{2}{3}(1-b)}$
$a^{\small{\frac{2}{3}}}<-\cfrac{2}{3}(1-b)$
$\cfrac{3}{2}a^{\small{\frac{2}{3}}}<b-1$
$b>1+\cfrac{3}{2}a^{\small{\frac{2}{3}}}$ (答え)
SNSでシェア