複素数を極形式にして三角関数の最大・最小を求める(東京都立大2020理学部第3問)

$\alpha=\cfrac{1+i}{2}$ とする。ただし，$i$ は虚数単位を表し，複素数 $z$ と共役な複素数を $\bar{z}$ で表す。以下の問いに答えなさい。（東京都立大2020）

(1) 複素数 $z$ に対し，$\bar{\alpha}z+\alpha\bar{z}$ は実数になることを示しなさい。

(2) 複素数平面上で点 $w$ が円 $|w|=1$ 上を動くとき，点 $z=4w+\cfrac{3}{w}$ の描く図形を求めなさい。

(3) 点 $z$ が(2)で求めた図形の上を動くとき，$\bar{\alpha}z+\alpha\bar{z}$ の最大値と最小値を求めなさい。また，そのときの $z$ の値を求めなさい。

複素数を x+yi で表す

(1)から始めます。

ここは複素数を $x+yi$ と表してみましょう。

$\alpha=\cfrac{1}{2}(1+i)$ のとき，その共役な複素数は

$\bar{\alpha}=\cfrac{1}{2}(1-i)$ となるので

$\bar{\alpha}z+\alpha\bar{z}$
$=\cfrac{1}{2}(1-i)(x+yi)+\cfrac{1}{2}(1+i)(x-yi)$
$=\cfrac{1}{2}(x+yi-xi+y+x-yi+xi+y)$
$=\cfrac{1}{2}(2x+2y)$
$=x+y$　・・・①

（証明終わり）

式から虚数の $i$ が消えたということは，この式は実数であるということです。

極形式になおす

(2)に進みます。

この問題は，実はこの辺りから複素数平面というより，媒介変数表示の設問に変わってしまいます。

$|w|=1$ より，両辺を 2 乗して

$|w|^2=1$
$w\bar{w}=1$
$\bar{w}=\cfrac{1}{w}$

よって

$z=4w+\cfrac{3}{w}$
$=4w+3\bar{w}$ ・・・②

$w$ を極形式で表すと

$w=\cos\theta+i\sin\theta$

また

$\bar{w}=\cos\theta-i\sin\theta$

となるので，これらを②に代入すると

$z=4(\cos\theta+i\sin\theta)+3(\cos\theta-i\sin\theta)$
$=7\cos\theta+i\sin\theta$

たとえば，$\theta=0$ のとき，$z=7$ となるので，平面座標では (7,0) です。$\theta=\cfrac{\pi}{2}$ なら，$z=i$ だから，(0,1)。$\theta=\pi$ なら，$z=-7$ だから， $(-7,0)$。

こうして考えていくと，楕円ができあがります。

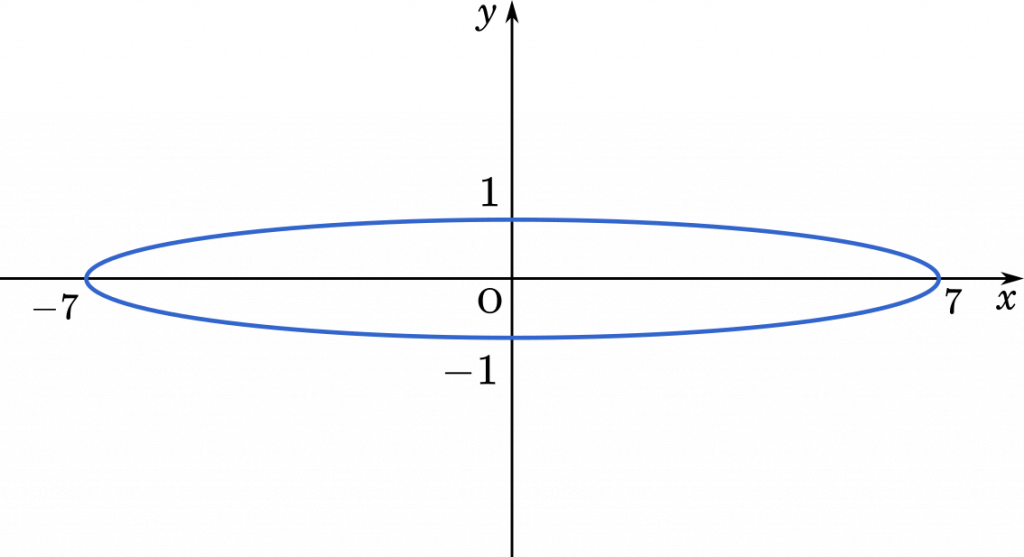
したがって，楕円の式は

$\cfrac{x^2}{7^2}+y^2=1$　（答え）

三角関数の合成

(3)に進みます。

(1)を振り返ると，$\bar{\alpha}z+\alpha\bar{z}$ は実数で $=x+y$ でした。これはもともと $z=x+yi$ としていたことを思い出しましょう。

また，(2)で $z=7\cos\theta+i\sin\theta$ となったので

$x=7\cos\theta$，$y=\sin\theta$

となります。

話をまとめると

$\bar{\alpha}z+\alpha\bar{z}=7\cos\theta+\sin\theta$

ということになります。

ここから，三角関数の合成を行います。

$=5\sqrt{2}\sin(\theta+t)$

最大となるのは $\sin(\theta+t)=1$ のとき，$5\sqrt{2}$

$\theta+t=\cfrac{\pi}{2}$
$\theta=\cfrac{\pi}{2}-t$

三角関数の合成で作った $t$ の値の範囲は $0<t<\cfrac{\pi}{2}$ です。

単位円を描いてみると，三角比の相互の関係がつかめるでしょう。

$\sin\Big(\cfrac{\pi}{2}-t\Big)=\cos t$
$\cos\Big(\cfrac{\pi}{2}-t\Big)=\sin t$

となるので

$z=7\sin t+i\cos t=\cfrac{7\cdot7}{5\sqrt{2}}+\cfrac{i}{5\sqrt{2}}$
$=\cfrac{\sqrt{2}(49+i)}{10}$

次に最小値を求めると

最小となるのは $\sin(\theta+t)=-1$ のとき $-5\sqrt{2}$

$\theta+t=\cfrac{3\pi}{2}$
$\theta=\cfrac{3\pi}{2}-t$

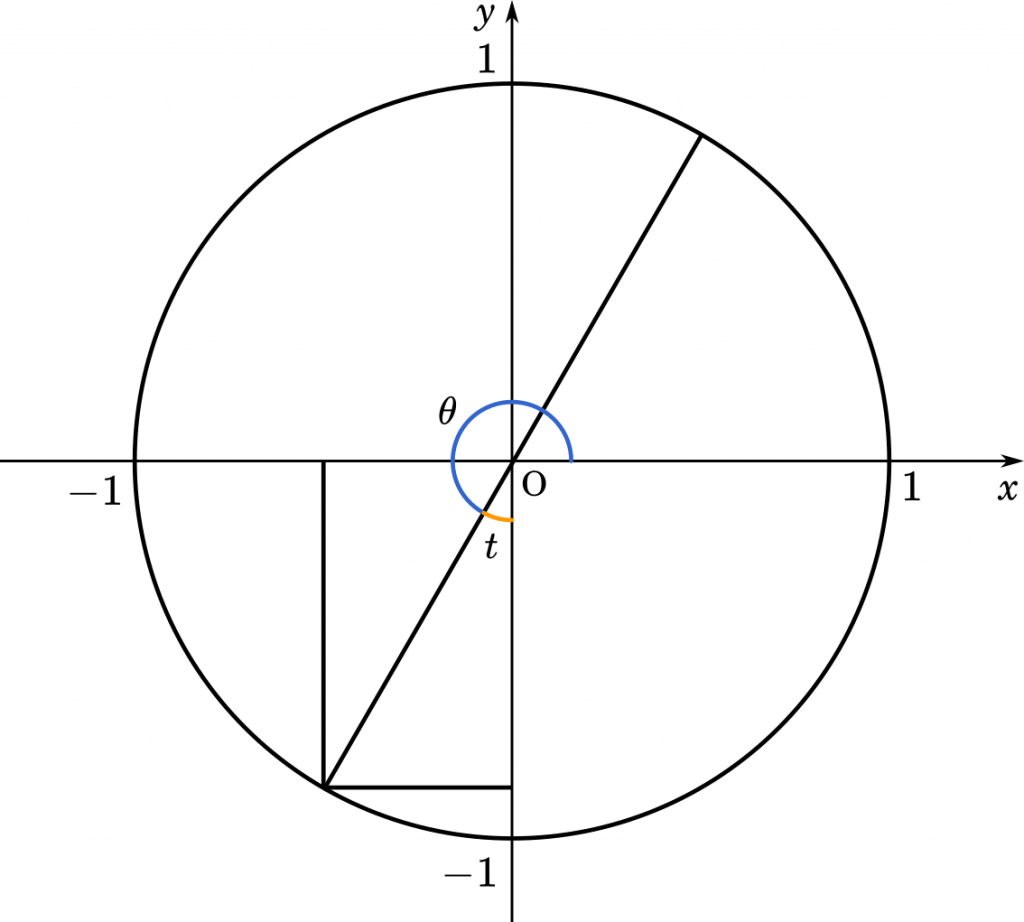
$\sin\Big(\cfrac{3\pi}{2}-t\Big)=-\cos t$
$\cos\Big(\cfrac{3\pi}{2}-t\Big)=-\sin t$
$z=7\sin t+\cos t$
$=-\cfrac{7\cdot7}{5\sqrt{2}}-\cfrac{i}{5\sqrt{2}}$
$=-\cfrac{\sqrt{2}(49+i)}{10}$

したがって

$z=\cfrac{\sqrt{2}(49+i)}{10}$ のとき，最大値 $5\sqrt{2}$

$z=-\cfrac{\sqrt{2}(49+i)}{10}$ のとき，最小値 $-5\sqrt{2}$　（答え）