【IIBベクトル】ベクトルと平行四辺形・辺が平行／垂直のとき(東京都立大2015文系第2問)

平行四辺形 ABCD において，AD = 6，∠A = 120°，$\overrightarrow{\text{AD}}=\vec{a}$，$\overrightarrow{\text{AB}}=\vec{b}$，AB = $x$ とする。点 A から直線 CD に対線 AP を引き，点 A を通り辺 AD に垂直な直線と対角線 BD の交点を Q とする。このとき，以下の問いに答えなさい。（東京都立大2015）

(1) 線分 AP の長さを求めなさい。

(2) $\overrightarrow{\text{AQ}}$ を $\vec{a}$，$\vec{b}$，$x$ の式で表しなさい。

(3) AP = AQ が成り立つときの辺 AB の長さを求めなさい。

(4) 線分 PQ と辺 AD が平行になるときの辺 AB の長さを求めなさい。

三角定規の辺の比

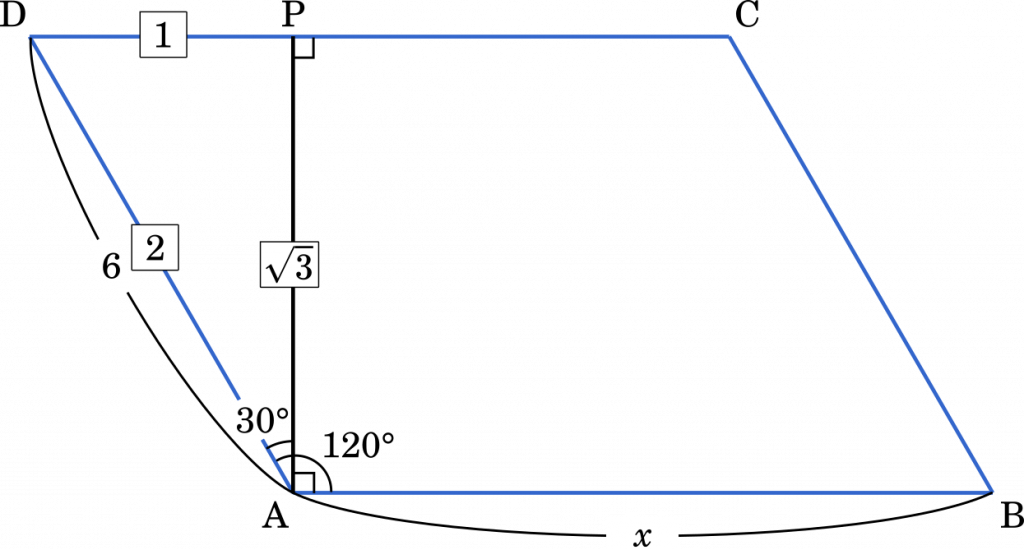
(1)から始めます。

△ADP は辺の比が $1:2:\sqrt{3}$ の直角三角形になります。よって
AP = $6\times\cfrac{\sqrt{3}}{2}=3\sqrt{3}$　（答え）

垂直な辺を利用して内分点を求める

(2)に進みます。

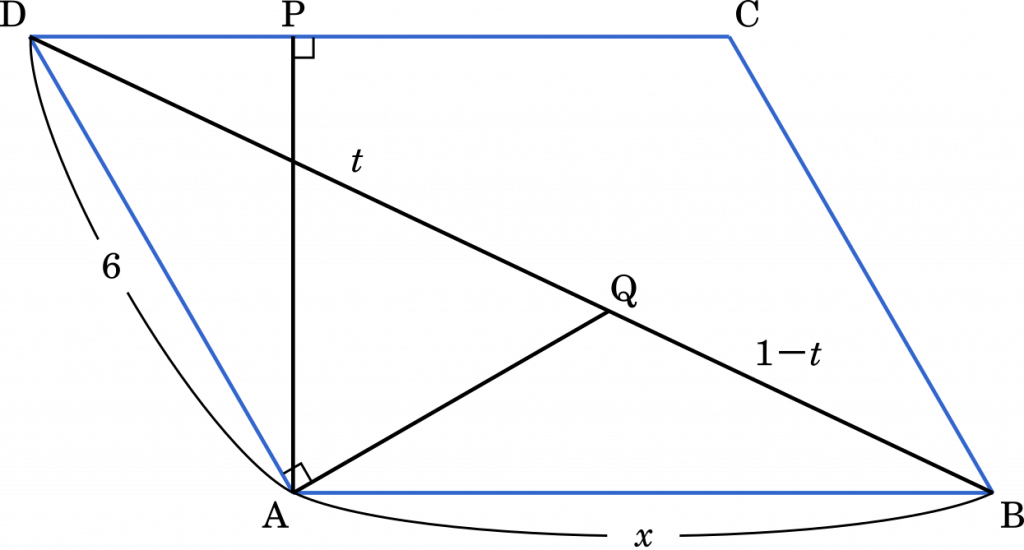
内分点を求めるときは，直線を $t:1-t$ に内分すると良いでしょう。

$\overrightarrow{\text{AQ}}=(1-t)\vec{a}+t{b}$ ・・・①　として

$\text{AD}\perp\text{AQ}$ より

$\vec{a}\cdot\overrightarrow{\text{AQ}}=0$
$\vec{a}\{(1-t)\vec{a}+t\vec{b}\}=0$
$(1+t)|\vec{a}|^2+t\vec{a}\cdot\vec{b}=0$

ここで

$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos120\degree$
$=6x\Big(-\cfrac{1}{2}\Big)$
$=-3x$

だから

$36(1+t)-3xt=0$
$36-36t-3xt=0$
$12-12t-xt=0$
$(12+x)t=12$
$t=\cfrac{12}{12+x}$

①に代入して

$\overrightarrow{\text{AQ}}=\Big(1-\cfrac{12}{12+x}\Big)\vec{a}+\cfrac{12}{12+x}\vec{b}$
$=\cfrac{12+x-12}{12+x}\vec{a}+\cfrac{12}{12+x}\vec{b}$
$=\cfrac{x}{12+x}\vec{a}+\cfrac{12}{12+x}\vec{b}$　（答え）

ベクトルの長さを求める

(3)に進みます。ベクトルの長さは 2 乗すると求めることができます。

AQ = AP より

$|\overrightarrow{\text{AQ}}|^2=\cfrac{x^2}{(12+x)^2}|\vec{a}|^2+2\cfrac{x}{12+x}\cdot\cfrac{12}{12+x}\space\vec{a}\cdot\vec{b}+\cfrac{144}{(12+x)^2}|\vec{b}|^2$
$=\cfrac{36x^2-72x^2+144x^2}{(12+x)^2}$
$\cfrac{108x^2}{(12+x)^2}=(3\sqrt{3})^2$
$108x^2=27(12+x)^2$
$4x^2=(12+x)^2$
$4x^2=144+24x+x^2$
$3x^2-24x-144=0$
$x^2-8x-48=0$
$(x-12)(x+4)=0$
$x>0$ より
$x=12$　（答え）

平行な辺を利用して直角三角形を見つける

(4)に進みます。

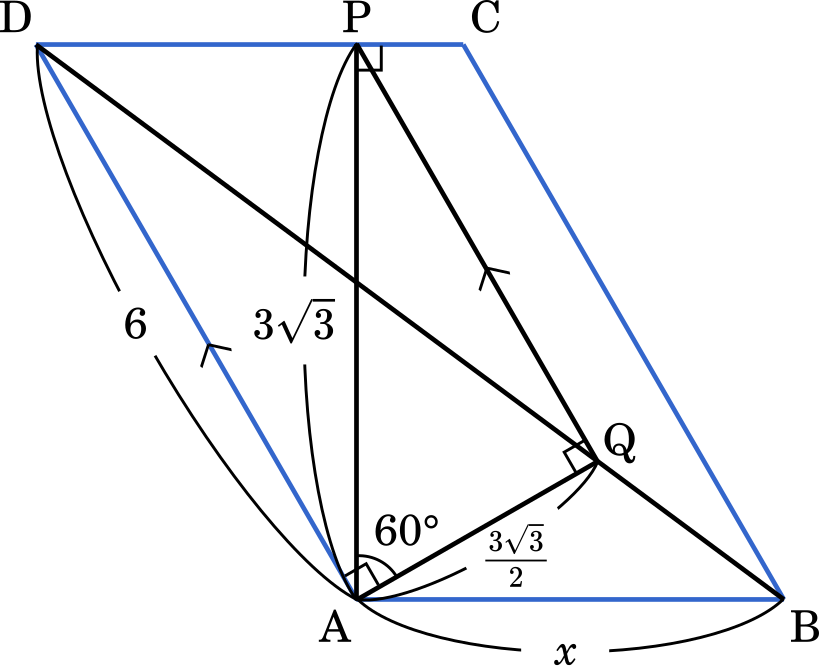
PQ // AD の関係を図に描いてみると，△APQ は辺の比が $1:2:\sqrt{3}$ の直角三角形になります。

したがって，AP = $3\sqrt{3}$ より，AQ = $\cfrac{3\sqrt{3}}{2}$ です。

あとは，これを(3)で作った式に代入して $x$ を求めましょう。

$|\overrightarrow{\text{AQ}}|^2=\Big(\cfrac{3\sqrt{3}}{2}\Big)^2$ より

$\cfrac{108x^2}{(12+x)^2}=\cfrac{27}{4}$
$16x^2=(12+x)^2$
$16x^2=144+24x+x^2$
$15x^2-24x-144=0$
$5x^2-8x-48=0$
$(5x+12)(x-4)=0$

$x>0$ より

$x=4$　（答え）