【スマホで読む・わかりやすい】センター数学IA2016本試【解説・正解・問題】

第5問　解答・解説

ア 0　イ ウ 1 2　エ オ 1 3　カ 3

キ ク 2 7　ケ 4　コサ 30　シ 2

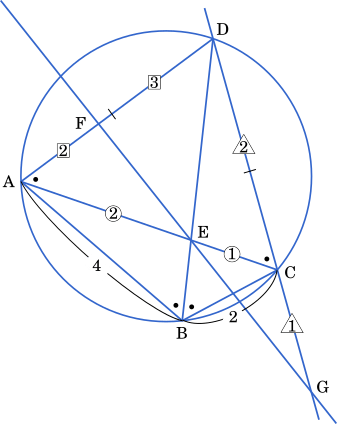
円周角の定理より ∠DAC = ∠DBC

また，長さの等しい弦から作られる円周角の大きさは同じだから，∠DAC = ∠DBC = ∠DCA

・・・ア

このことより，BE は ∠ABC の二等分線であることが分かる。角の二等分線と辺の比より，EC : AE = 2 : 4。したがって

$\cfrac{\text{EC}}{\text{AE}}=\cfrac{2}{4}=\cfrac{1}{2}$

・・・イウ

次に，メネラウスの定理より

$\cfrac{\text{AF}}{\text{FD}}\cdot\cfrac{\text{DG}}{\text{GC}}\cdot\cfrac{\text{CE}}{\text{EA}}=1$

$\cfrac{2}{3}\cdot\cfrac{\text{DG}}{\text{GC}}\cdot\cfrac{1}{2}=1$

$\cfrac{\text{DG}}{\text{GC}}=3$

$\cfrac{\text{GC}}{\text{DG}}=\cfrac{1}{3}$

・・・エオ

(1)

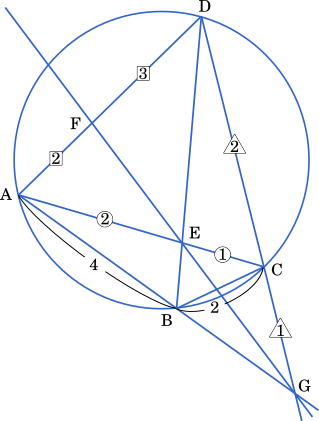
チェバの定理より

$\cfrac{\text{GB}}{\text{BA}}\cdot\cfrac{\text{AF}}{\text{FD}}\cdot\cfrac{\text{DC}}{\text{CG}}=1$

$\cfrac{\text{GB}}{\text{BA}}\cdot\cfrac{2}{3}\cdot\cfrac{2}{1}=1$

$\cfrac{\text{GB}}{\text{BA}}=\cfrac{3}{4}$

よって，GB : BA = 3 : 4

したがって，

BG = $4\cdot\cfrac{3}{4}=3$

・・・カ

また，方べきの定理より

GB・GA = GC・GD

ここで

GC = $\cfrac{1}{2}$ DC

GD = $\cfrac{3}{2}$ DC

だから

$3\cdot7=\cfrac{1}{2}\text{DC}\cdot\cfrac{3}{2}\text{DC}$

$\cfrac{3}{4}\text{DC}^2=21$

$\text{DC}^2=28$

DC = $2\sqrt{7}$

・・・キク

(2)

△ABC について考えると，外接円の直径は 4 より小さくなることはない。直径を 4 とすると，AB が直径になる。

・・・ケ

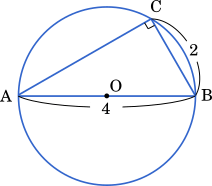
このとき，∠ACB = $90\degree$ となり △ABC は，$1:2:\sqrt{3}$ の直角三角形である。したがって

∠BAC = $30\degree$

・・・コサ

また，AH を求めると

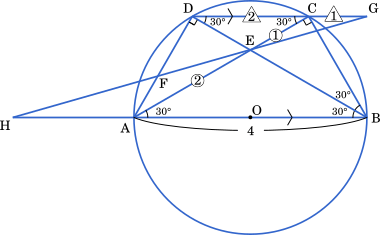
円周角の定理より ∠BAC = ∠BDC = $30\degree$

∠ACB = $60\degree$ かつ ∠ABD = ∠CBD より

∠ABD = ∠CBD = $30\degree$

円周角の定理より ∠ABD = ∠ACD = $30\degree$

∠BAC = ∠ACD となり錯角が等しいから DG // AB

よって

△ABE ∽ △CDE, △HAE ∽ △GCE

が成り立つ。

AE : CE = 2 : 1 より

DC = $\cfrac{1}{2}$ AB = $2$

DC : CG = 2 : 1 より

CG = $\cfrac{1}{2}$ DC = $1$

また，HA : GC = 2 : 1 より

HA = 2CG = $2$

・・・シ

第5問　問題文

四角形 ABCD において, AB = 4, BC = 2, DA = DC であり, 4つの頂点 A, B, C, D は同一円周上にある。対角線 AC と対角線 BD の交点を E, 線分 AD を 2 : 3 の比に内分する点を F, 直線 FE と直線 DC の交点を G とする。

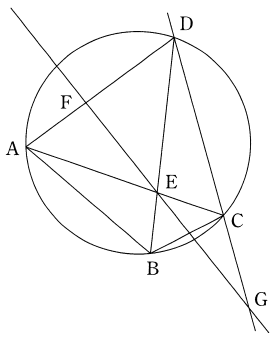
参考図

次の $\boxed{\text{ア}}$ には, 下の⓪~④のうちから当てはまるものを一つ選べ。

∠ABC の大きさが変化するとき四角形 ABCD の外接円の大きさも変化することに注意すると, ∠ABC の大きさがいくらであっても, ∠DAC と大きさが等しい角は, ∠DCA と ∠DBC と $\boxed{\text{ア}}$ である。

⓪ ∠ABD　① ∠ACB　② ∠ADB

③ ∠BCG　④ ∠BEG

このことより $\cfrac{\text{EC}}{\text{AE}}=\cfrac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}$ である。次に, △ACD と直線 FE に着目すると, $\cfrac{\text{GC}}{\text{DG}}=\cfrac{\boxed{\text{エ}}}{\boxed{\text{オ}}}$ である。

(1) 直線 AB が点 G を通る場合について考える。

このとき, △AGD の辺 AG 上に点 B があるので, BG = $\boxed{\text{カ}}$ である。

また, 直線 AB と直線 DC が点 G で交わり, 4点 A, B, C, D は同一円周上にあるので, DC = $\boxed{\text{キ}}\sqrt{\boxed{\text{ク}}}$ である。

(2) 四角形 ABCD の外接円の直径が最小となる場合について考える。

このとき, 四角形 ABCD の外接円の直径は $\boxed{\text{ケ}}$ であり, ∠BAC = $\boxed{\text{コサ}}\degree$ である。

また, 直線 FE と直線 AB の交点を H とするとき, $\cfrac{\text{GC}}{\text{DG}}=\cfrac{\boxed{\text{エ}}}{\boxed{\text{オ}}}$ の関係に着目して AH を求めると, AH = $\boxed{\text{シ}}$ である。