【スマホで読む・わかりやすい】センター数学IA2018本試【解説・正解・問題】

第1, 2問必答。第3~5問はいずれか2問を選択し, 解答。

第1問　解答・解説

ア 5　イ,ウエ 6,14　オ 2　カ 8　キ 2

ク 0　ケ 2　コ 0　サ シ 1 3　ス 1

セ 1　ソ タ 4 5　チ ツテ ト 7 13 4

$(x+n)(n+5-x)$ を展開すると

$=(x+n)\{n+(5-x)\}$

$=nx+x(5-x)+n^2+n(5-x)$

$=x(5-x)+n^2+n(x+5-x)$

$=x(5-x)+n^2+5n$

・・・ア

$X=x(5-x)=5x-x^2$ とおくと

$(x+1)(6-x)=6x-x^2+6-x$

$=5x-x^2+6=X+6$

$(x+2)(7-x)=7x-x^2+14-2x$

$=5x-x^2+14=X+14$

したがって

$A=X(X+6)(X+14)$

・・・イウエ

また，$x=\cfrac{5+\sqrt{17}}{2}$ のとき

$X=\cfrac{5+\sqrt{17}}{2}\Big(5-\cfrac{5+\sqrt{17}}{2}\Big)$

$=\cfrac{5+\sqrt{17}}{2}\Big(\cfrac{10-5-\sqrt{17}}{2}\Big)$

$=\cfrac{5+\sqrt{17}}{2}\Big(\cfrac{5-\sqrt{17}}{2}\Big)$

$=\cfrac{25-17}{4}=2$

・・・オ

$A=2(2+6)(2+14)=2\cdot8\cdot16$

$=2\cdot2^3\cdot2^4=2^8$

・・・カ

〔2〕

(1)

(a) $A$ ⊂ $C$

$A$ は 20 以下の自然数のうち 20 の約数だから

$A$＝｛ 1, 2, 4, 5, 10 ,20｝

$C$ は 20 以下の自然数のうち偶数だから

$C$＝｛2, 4, 6, 8, 10, 12, 14, 16, 18, 20｝

1 と 5 は $C$ に含まれないので，誤り。

(b) $A$ ∩ $B$ ＝ $\varnothing$

$B$ は 20 以下の自然数のうち 3 の倍数だから

$B$＝｛3, 6, 9, 12, 15 ,18｝

$A$ に 3 の倍数は含まれないので，$A$，$B$ どちらにも含まれる要素はない。よって，正しい。

・・・キ

(c) ($A$ ∪ $C$) ∩ $B$ ＝｛6, 12, 18｝

($A$ ∪ $C$) ∩ $B$ は $A$ または $C$ のうち 3 の倍数だから，6, 12, 18 である。よって，正しい。

(d) ($\overline{A}$ ∩ $C$) ∪ $B$ ＝ $\overline{A}$ ∩ ($B$ ∪ $C$)

$\overline{A}$ ∩ $C$ は 20 以下の偶数のうち 20 の約数でないものだから

$(\overline{A}$ ∩ $C$)＝｛6, 8, 12, 14, 16, 18, 20｝

よって

($\overline{A}$ ∩ $C$) ∪ $B$ ＝｛3, 6, 8, 9, 12, 14, 15, 16, 18, 20｝

また，$\overline{A}$ ∩ ($B$ ∪ $C$) は 20 以下の偶数または 3 の倍数のうち 20 の約数でないものだから

$\overline{A}$ ∩ ($B$ ∪ $C$)＝｛3, 6, 8, 9, 12, 14, 15, 16, 18, 20｝

よって，正しい。

・・・ク

(2)

($q$ または $r$) $\implies$ $p$ を考えると

$p$：$|x-2|$ ＞ 2

$x$ ≧ 2 のとき，$x-2$ ＞ 2 だから $x$ ＞ 4

$x$ ＜ 2 のとき，$-x+2$ ＞ 2 だから $x$ ＜ 0

よって，真。

また，$p$ $\implies$ ($q$ または $r$) も真。

したがって，$q$ または $r$ であることは，$p$ であるための必要十分条件。

・・・ケ

次に，$s\implies r$ を考えると

$s$：$\sqrt{x^2}$ ＞ 4

$x^2$ ＞ 16

$x^2-16$ ＞ 0

$(x+4)(x-4)$ ＞ 0

$x$ ＜ －4，$x$ ＞ 4

よって，偽。

また，$s\implies r$ は真。

したがって，$s$ は $r$ であるための必要条件であるが，十分条件ではない。

・・・コ

〔3〕

式を平方完成すると

$f(x)=ax^2-2(a+3)x-3a+21$

$=a\Big\{x^2-\cfrac{2}{a}(a+3)x\Big\}-3a+21$

$=a\Big(x-\cfrac{a+3}{a}\Big)^2-\cfrac{(a+3)^2}{a}-3a+21$

$=a\Big(x-1-\cfrac{3}{a}\Big)^2-a-6-\cfrac{9}{a}-3a+21$

$=a\Big(x-1-\cfrac{3}{a}\Big)^2-4a-\cfrac{9}{a}+15$

したがって，$p=1+\cfrac{3}{a}$

・・・サシ

$f(x)$ の最小値が $f(4)$ のとき $p$ ≧ 4

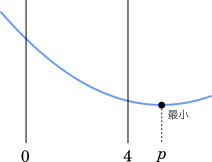
$1+\cfrac{3}{a}$ ≧ 4

$\cfrac{3}{a}$ ≧ 3

$\cfrac{1}{a}$ ≧ 1

$a$ ≦ 1

$a$ は正の実数だから

0 ＜ $a$ ≦ 1

・・・ス

また，$f(x)$ の最小値が $f(p)$ のとき $0$ ≦ $p$ ≦ 4

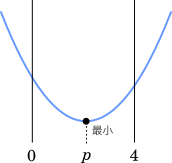
0 ≦ $1+\cfrac{3}{a}$ ≦ 4

－1 ≦ $\cfrac{3}{a}$ ≦ 3

不等式を分けて考えると

－1 ≦ $\cfrac{3}{a}$

$-a$ ≦ 3

$a$ ≧ －3

また

$\cfrac{3}{a}$ ≦ 3

$\cfrac{1}{a}$ ≦ 1

1 ≦ $a$

2 つを合わせると，1 ≦ $a$

・・・セ

$f(x)$ の最小値が 1 になるとき

(i) 0 ＜ $a$ ≦ 1 のとき

$f(4)=16a-8(a+3)-3a+21=1$

$5a-3=1$

$a=\cfrac{4}{5}$

・・・ソタ

(ii) 1 ≦ $a$ のとき

$f(p)$ の頂点の $y$ 座標は $-4a-\cfrac{9}{a}+15$ だから

$-4a-\cfrac{9}{a}+15=1$

$4a+\cfrac{9}{a}-14=0$

$4a^2-14a+9=0$

$a=\cfrac{7\pm\sqrt{49-36}}{4}$

$=\cfrac{7\pm\sqrt{13}}{4}$

・・・チツテト

第1問　問題文

〔1〕$x$ を実数とし

$A＝x(x+1)(x+2)(5-x)(6-x)(7-x)$

とおく。整数 $n$ に対して

$(x+n)(n+5-x)=x(5-x)+n^2+\boxed{\text{ア}}n$

であり，したがって，$X=x(5-x)$ とおくと

$A=X(X+\boxed{\text{イ}})(X+\boxed{\text{ウエ}})$

と表せる。

$x=\cfrac{5+\sqrt{17}}{2}$ のとき，$X＝\boxed{\text{オ}}$ であり，$A＝2^{\boxed{\text{カ}}}$ である。

〔2〕

(1) 全体集合 $U$ を $U＝\{x|x$ は 20 以下の自然数$\}$とし，次の部分集合 $A, B, C$ を考える。

$A$ ＝｛$x$｜$x$∈$U$ かつ $x$ は 20 の約数｝

$B$ ＝｛$x$｜$x$∈$U$ かつ $x$ は 3 の倍数｝

$C$ ＝｛$x$｜$x$∈$U$ かつ $x$ は偶数｝

集合 $A$ の補集合を $\overline{A}$ と表し，空集合を $\varnothing$ と表す。

次の $\boxed{\text{キ}}$ に当てはまるものを，下の⓪～③のうちから一つ選べ。

集合の関係

(a) $A$ ⊂ $C$

(b) $A$ ∩ $B$＝$\varnothing$

の正誤の組合せとして正しいものは $\boxed{\text{キ}}$ である。

$\def\arraystretch{1.25}\begin{array}{c:c:c:c:c}&\text{⓪}&\text{①}&\text{②}&\text{③}\\\hline（a)&\text{正}&\text{正}&\text{誤}&\text{誤}\\（b）&\text{正}&\text{誤}&\text{正}&\text{誤}\end{array}$

次の $\boxed{\text{ク}}$ に当てはまるものを，下の⓪～③のうちから一つ選べ。

集合の関係

(c)（$A$ ∪ $C$）∩ $B$＝｛6，12，18｝

(d)（$\overline{A}$ ∩ $C$）∪ $B$＝$\overline{A}$ ∩（$B$ ∪ $C$）

の正誤の組合せとして正しいものは $\boxed{\text{ク}}$ である。

$\def\arraystretch{1.25}\begin{array}{c:c:c:c:c}&\text{⓪}&\text{①}&\text{②}&\text{③}\\\hline（c）&\text{正}&\text{正}&\text{誤}&\text{誤}\\（d）&\text{正}&\text{誤}&\text{正}&\text{誤}\end{array}$

(2) 実数 $x$ に関する次の条件 $p,q,r,s$ を考える。

$p$：｜$x$－2｜＞ 2，$q$：$x$ ＜ 0，

$r$：$x$ ＞ 4，$s$：$\sqrt{x^2}$ ＞ 4

次の $\boxed{\text{ケ}}$，$\boxed{\text{コ}}$ に当てはまるものを，下の⓪～③のうちからそれぞれ一つ選べ。ただし，同じものを繰り返し選んでもよい。

$q$ または $r$ であることは，$p$ であるための $\boxed{\text{ケ}}$。また，$s$ は $r$ であるための $\boxed{\text{コ}}$。

⓪ 必要条件であるが，十分条件ではない

① 十分条件であるが，必要条件ではない

② 必要十分条件である

③ 必要条件でも十分条件でもない

〔3〕$a$ を正の実数とし

$f(x)=ax^2-2(a+3)x-3a+21$

とする。2次関数 $y=f(x)$ のグラフの頂点の $x$ 座標を $p$ とおくと

$p=\boxed{\text{サ}}+\cfrac{\boxed{\text{シ}}}{a}$

である。

0 ≦ $x$ ≦ 4 における関数 $y=f(x)$ の最小値が $f(4)$ となるような $a$ の値の範囲は

0 ＜ $a$ ≦ $\boxed{\text{ス}}$

である。

また，0 ≦ $x$ ≦ 4 における関数 $y$ ＝ $f(x)$ の最小値が $f(p)$ となるような $a$ の値の範囲は

$\boxed{\text{セ}}$ ≦ $a$

である。

したがって，0 ≦ $x$ ≦ 4 における関数 $y$＝$f(x)$ の最小値が 1 であるのは

$a$＝$\cfrac{\boxed{\text{ソ}}}{\boxed{\text{タ}}}$ または $a$＝$\cfrac{\boxed{\text{チ}}+\sqrt{\boxed{\text{ツテ}}}}{\boxed{\text{ト}}}$

のときである。