【スマホで読む・わかりやすい】センター数学IA2018追試【解説・正解・問題】

第2問　解答・解説

ア イ 3 2　ウ 1　エ 2　オ カ キ 4 3 3

クケ コ サ 22 3 3　シ 5

ス,セ 4,5 (解答の順序は問わない)

ソ 4　タ 5

〔1〕

(1)

余弦定理より

$14^2=4^2+(10\sqrt{3})^2-2\cdot4\cdot10\sqrt{3}\cos$∠B

$196=16+300-80\sqrt{3}\cos$∠B

$80\sqrt{3}\cos$∠B＝120

$\cos$∠B＝$\cfrac{120}{80\sqrt{3}}=\cfrac{3}{2\sqrt{3}}=\cfrac{\sqrt{3}}{2}$

・・・アイ

正弦定理より

$2R=\cfrac{\text{AD}}{\sin\angle\text{B}}$

$\sin^2 x+\cos^2 x=1$ より

$\sin^2$∠B＋$\Big(\cfrac{\sqrt{3}}{2}\Big)^2=1$

$\sin^2$∠B＝$\cfrac{1}{4}$

$\sin$∠B＝$\cfrac{1}{2}$

値を代入して

$2R=\cfrac{\text{AD}}{\cfrac{1}{2}}=\cfrac{\text{AD}\times2}{\cfrac{1}{2}\times2}=$ 2AD

$\cfrac{\text{AD}}{R}=1$

・・・ウ

よって，AD＝$R$ となるので，AD の最小値は AD⊥BC のとき

AD＝$4\sin$∠B＝$4\cdot\cfrac{1}{2}=2$

したがって，$R$ の最小値は 2

・・・エ

(2)

△ABD の外接円の中心が BC 上にあるとき，BD は直径となるので，∠BAD＝90°

また，正弦定理より

$\cfrac{\text{AD}}{\sin\angle\text{B}}=\cfrac{\text{BD}}{\sin\angle\text{BAD}}$

BD＝2 $R$ ＝1 だから

$\cfrac{\text{AD}}{\cfrac{1}{2}}=\cfrac{\text{BD}}{1}$

$\cfrac{\text{AD}\times2}{\cfrac{1}{2}\times2}=\cfrac{\text{BD}}{1}$

2AD＝BD

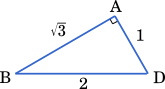
△ABD は辺の比が 1 : 2 : $\sqrt{3}$ の直角二等辺三角形となるので

AB：BD＝$\sqrt{3}$：2

4：BD＝$\sqrt{3}$：2

$\sqrt{3}$BD＝8

BD＝$\cfrac{8}{\sqrt{3}}=\cfrac{8\sqrt{3}}{3}$

BD は直径だから $R=\cfrac{4\sqrt{3}}{3}$

・・・オカキ

さらに，△ACDの面積を求めると

底辺の長さは

$10\sqrt{3}-\cfrac{8\sqrt{3}}{3}=\cfrac{22\sqrt{3}}{3}$

∠B＝30°を用いて，高さは

$4\sin$∠B＝$4\cdot\cfrac{1}{2}=2$

したがって

△ACD＝$\cfrac{1}{2}\cdot\cfrac{22\sqrt{3}}{3}\cdot2=\cfrac{22\sqrt{3}}{3}$

・・・クケコサ

〔2〕

(1)

$x$ と $y$ の共分散を $s_{xy}$，$x$，$y$ の標準偏差をそれぞれ $s_x$，$s_y$ とすると相関係数 $r$ は $r=\cfrac{s_{xy}}{s_xs_y}$

$r=\cfrac{s_{XY}}{s_Xs_Y}$

$=\cfrac{0.0263}{0.105\times0.260}=0.96\cdots$

したがって，0.91 ＜ $r$

・・・シ

(2)

⓪ 期間 A における最大値は期間 B における最大値より大きい。よって誤り。

① 期間 A における第1四分位数は，期間 B における第1四分位数より大きい。よって誤り。

② 期間 A における四分位範囲と期間 B における四分位範囲の差は 0.2 より小さい。よって誤り。

③ 期間 A における範囲は，期間 B における範囲より大きい。よって誤り。

④ 絶対値は 0 と中央値の間の距離であり，期間 A，期間 B の両方において，距離を 8 倍しても四分位範囲より小さい。よって正しい。

⑤ 期間 A の第3四分位数は 0.4。ヒストグラムを見ると度数が最大の階級は 0 以上 0.5 未満だから，正しい。

⑥ 期間 B の第3四分位数は －0.4 以上 －0.2 未満。ヒストグラムを見ると，度数が最大の階級は 0 以上 0.5 未満だから，誤り。

・・・スセ

(3)

$X$ の平均を $\overline{X}$，$X’$ の平均を $\overline{X’}$ とすると

$\overline{X’}=\cfrac{1}{n}(aX_1+b+aX_2+b+\cdots+aX_n+b)$

$=a\cdot\cfrac{1}{n}(X_1+X_2+\cdots+X_n)+\cfrac{1}{n}\cdot nb$

$=a\overline{X}+b$

よって，$\overline{X’}=a\overline{X}+b$，$\overline{Y’}=c\overline{Y}+d$ が成り立つ。

$X$ と $Y$ の共分散を $s_{XY}$ とすると

$s_{XY}=\cfrac{1}{n}\{(X_1-\overline{X})(Y_1-\overline{Y})+\cdots+(X_n-\overline{X})(Y_n-\overline{Y})\}$

$X’$ と $Y’$ の共分散を $s_{X’Y’}$ とすると

$s_{X’Y’}=\cfrac{1}{n}\{({X_1}’-\overline{X’})({Y_1}’-\overline{Y’})+\cdots+({X_n}’-\overline{X’})({Y_n}’-\overline{Y’})\}$

$=\cfrac{1}{n}\{(aX_1+b-a\overline{X}-b)(cY_1+d-c\overline{Y}-d)+\cdots+(aX_n+b-a\overline{X}-b)(cY_n+d-c\overline{Y}-d)\}$

$=\cfrac{1}{n}\{(aX_1-a\overline{X})(cY_1-c\overline{Y})+\cdots+(aX_n-a\overline{X})(cY_n-c\overline{Y})\}$

$=ac\cfrac{1}{n}\{(X_1-\overline{X})(Y_1-\overline{Y})+\cdots+(X_n-\overline{X})(Y_n-\overline{Y})\}$

$=ac\cdot s_{XY}$

$X$，${X’}$ の分散をそれぞれ ${s_X}^2$，${s_{X’}}^2$ とすると

${s_X}^2=\cfrac{1}{n}\{(X_1-\overline{X})^2+\cdots+(X_n-\overline{X})^2\}$

${s_{X’}}^2=\cfrac{1}{n}\{({X_1}’-\overline{X’})^2+\cdots+({X_n}’-\overline{X’})^2\}$

$=\cfrac{1}{n}\{(aX_1+b-a\overline{X}-b)^2+\cdots+(aX_n+b-a\overline{X}-b)^2\}$

$=\cfrac{1}{n}\{(aX_1-a\overline{X})^2+\cdots+(aX_n-a\overline{X})^2\}$

$=a^2\cfrac{1}{n}\{(X_1-\overline{X})^2+\cdots+(X_n-\overline{X})^2\}$

$=a^2\cdot {s_X}^2$

ここで，標準偏差は正の値を取ることに注意して

${s_X}’=|a|s_X$

同様に ${s_Y}’=|c|s_Y$

$X$ と $Y$ の相関係数を $r_1$ とすると

$r_1=\cfrac{s_{XY}}{s_Xs_y}$

$X’$ と $Y’$ の相関係数を $r_1$ とすると

$r_2=\cfrac{s_{X’Y’}}{{s_X}'{s_Y}’}$

$=\cfrac{ac\cdot s_{XY}}{|a|s_X\cdot |c|s_Y}$

$=\cfrac{ac}{|ac|}$

・・・ソ

(4)

散布図1は三つの散布図のうち最も正の相関が強いので，$r_1=0.98$。また散布図3は負の相関があるので，$r_3=-0.76$。したがって，⑤が正しい。

・・・タ

第2問　問題文

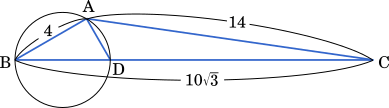
〔1〕△ABC は AB＝4，BC＝$10\sqrt{3}$，AC＝14 を満たす。

(1) $\cos$∠B＝$\cfrac{\sqrt{\boxed{\text{ア}}}}{\boxed{\text{イ}}}$ である。辺 BC 上に点 D を取り，△ABD の外接円の半径を $R$ とするとき，$\cfrac{\text{AD}}{R}=\boxed{\text{ウ}}$ であり，点 D を点 B から点 C まで移動させるとき，$R$ の最小値は $\boxed{\text{エ}}$ である。ただし，点 D は点 B とは異なる点とする。

(2) △ABD の外接円の中心が辺 BC 上にあるとき，

$R=\cfrac{\boxed{\text{オ}}\sqrt{\boxed{\text{カ}}}}{\boxed{\text{キ}}}$ であり，△ACD の面積は $\cfrac{\boxed{\text{クケ}}\sqrt{\boxed{\text{コ}}}}{\boxed{\text{サ}}}$ である。

〔2〕高校生の K さんは，ニュースで「為替レート（1米ドルは何円か）」および「日経平均株価」と呼ばれている数値が日々変化していることに興味をもったので，これらの数値を入手して調べてみることにした。

為替レートを 100 で割ったものを $X$ とする。例えば，1米ドルが 123 円のとき $X$ は 1.23 となる。また，日経平均株価を 10,000 で割ったものを $Y$ とする。例えば，日経平均株価が 16,500 円のとき $Y$ は 1.65 となる。

図1は，$X$，$Y$ の日々の変化を描いたものである。ただし，土曜日，日曜日，祝日などデータのない日は除いている。全期間を次の二つの期間に分けて考察する。

期間A：2013 年 1 月 4 日～ 2014 年 11 月 28 日（468 日分のデータ）

期間B ：2014 年 12 月 1 日～ 2016 年 1 月 29 日（284 日分のデータ）

図2は，期間 A と期間 B における $X$，$Y$ のデータの散布図である。

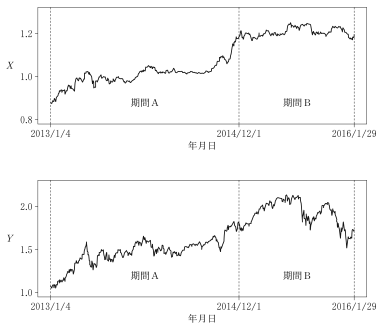
図1 $X$，$Y$ の日々の変化

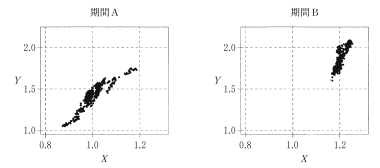
図2 $X$，$Y$ のデータの散布図

(1) 表1は，$X$ と $Y$ について平均値，標準偏差および共分散を計算し，有効数字 3 桁で表したものである。ただし，$X$ と $Y$ の共分散とは，$X$ の偏差と $Y$ の偏差の積の平均値である。

表1 平均値，標準偏差および共分散

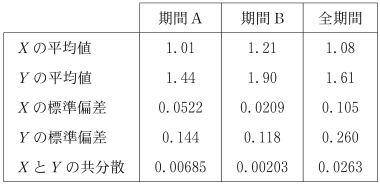
次の $\boxed{\text{シ}}$ に当てはまるものを，下の⓪～⑤のうちから一つ選べ。

表1を用いて，期間 A，期間 B における $X$ と $Y$ の相関係数を求め，小数第 3 位を四捨五入すると，それぞれ 0.91 と 0.82 である。全期間における $X$ と $Y$ の相関係数を $r$ とすると $\boxed{\text{シ}}$ である。

⓪ $r$ ≦ 0　① 0 ＜ $r$ ＜ 0.82

② $r=0.82$　③ 0.82 ＜ $r$ ＜ 0.91

④ $r=0.91$　⑤ 0.91 ＜ $r$

(2) $X$ のデータの $t$ 番目の値を $x_t$ とする。期間 A に対応するのは $t$＝1，2，$\cdots$，468 であり，期間 B に対応するのは $t$＝469，470，$\cdots$，752 である。$X$ が日々どのように変化しているか調べるために，次の式によって定義される $u_t$ を計算する。

$u_t$＝$\cfrac{x_{t+1}-x_t}{x_t}\times 100$

ただし，期間 A の最終日（$t$＝468）と期間 B の最終日（$t$＝752）については $u_t$ を計算しない。$u_1$，$\cdots$，$u_{467}$ および $u_{469}$，$\cdots$，$u_{751}$ を $U$ のデータと呼ぶ。

図3および図4は，期間 A，期間 B における $U$ のデータのヒストグラムおよび箱ひげ図である。期間 A における中央値は 0.0584 であり，期間 B における中央値は 0.0252 であった。

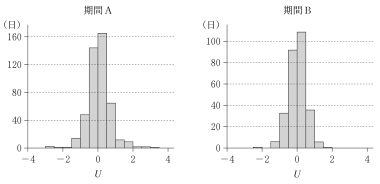
図3 $U$ のデータのヒストグラム

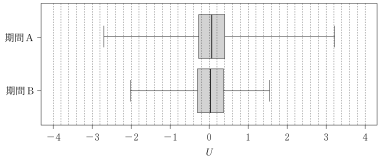
図4 $U$ のデータの箱ひげ図

次の $\boxed{\text{ス}}$，$\boxed{\text{セ}}$ に当てはまるものを，下の⓪～⑥のうちから一つずつ選べ。ただし，解答の順序は問わない。

図3および図4から $U$ のデータについて読み取れることとして正しいものは，$\boxed{\text{ス}}$，$\boxed{\text{セ}}$ である。

⓪ 期間 A における最大値は，期間 B における最大値より小さい。

① 期間 A における第1四分位数は，期間 B における第1四分位数より小さい。

② 期間 A における四分位範囲と期間 B における四分位範囲の差は 0.2 より大きい。

③ 期間 A における範囲は，期間 B における範囲より小さい。

④ 期間 A，期間 B の両方において，四分位範囲は中央値の絶対値の 8 倍より大きい。

⑤ 期間 A において，第3四分位数は度数が最大の階級に入っている。

⑥ 期間 B において，第1四分位数は度数が最大の階級に入っている。

(3) $X$，$Y$ から$X′$，$Y′$ を次の式によって定義する。

$X′$＝$aX+b$，$Y′=cY+d$

ただし，$a$，$b$，$c$，$d$ は定数であり，$a\not=0$ かつ $c\not=0$ とする。

次の $\boxed{\text{ソ}}$ に当てはまるものを，下の⓪～⑧のうちから一つ選べ。

$X′$ と $Y′$ の相関係数は，$X$ と $Y$ の相関係数の $\boxed{\text{ソ}}$ 倍である。

⓪ 1　① $a$　② $a^2$

③ $ac$　④ $\cfrac{ac}{|ac|}$　⑤ $b$

⑥ $b^2$　⑦ $bd$　⑧ $|bd|$

(4) 次ページの図5の三つの散布図について考える。散布図1で表される $V$ と $W$ の2種類のデータの相関係数，散布図2で表される $V′$ と $W′$ の2種類のデータの相関係数，および散布図3で表される$V″$ と $W″$ の2種類のデータの相関係数をそれぞれ $r_1$，$r_2$ および $r_3$ とする。これらは，小数第3位を四捨五入して小数第2位まで求めると，－0.76，0.10，0.98 のいずれかであることがわかっている。

次の $\boxed{\text{タ}}$ に当てはまるものを，下の⓪～⑤のうちから一つ選べ。

$r_1$，$r_2$ および $r_3$ の値の組合せとして正しいものは $\boxed{\text{タ}}$ である。

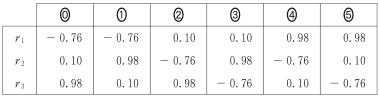
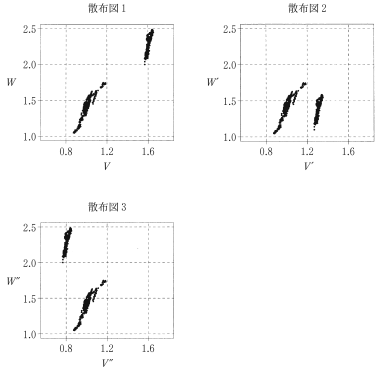
図5 三つの散布図