【スマホで読む・わかりやすい】センター数学IIB2013本試【解説・正解・問題】

第４問

OA$=5$，OC$=4$，∠AOC$=\theta$ である平行四辺形 OABC において，線分 OA を $3:2$ に内分する点を D とする。また，点 A を通り直線 BD に垂直な直線と直線 OC の交点を E とする。ただし，$0 < \theta < \pi$ とする。

以下，$\overrightarrow{\text{OA}}=\vec{a}$，$\overrightarrow{\text{OC}}=\vec{c}$ とおき，実数 $t$ を用いて $\overrightarrow{\text{OE}}=t\vec{c}$ と表す。

(1)　$t$ を $\cos\theta$ を用いて表そう。

$\overrightarrow{\text{AE}}=t\vec{c}-\vec{a}$，$\overrightarrow{\text{DB}}=\cfrac{\boxed{\text{ ア }}}{\boxed{\text{ イ }}}\vec{a}+\vec{c}$，$\vec{a}\cdot\vec{c}=\boxed{\text{ ウエ }}\cos\theta$

となるので，$\overrightarrow{\text{AE}}\cdot\overrightarrow{\text{DB}}=\boxed{\text{ オ }}$ により

$t=\cfrac{\boxed{\text{ カ }}(\boxed{\text{ キ }}\cos\theta+1)}{\boxed{\text{ ク }}(\cos\theta+\boxed{\text{ ク }})}$…①

となる。

(2)　点 E は線分 OC 上にあるとする。$\theta$ のとり得る値の範囲を求めよう。ただし，線分 OC は両端の点 O，C を含むものとする。以下，$r=\cos\theta$ とおく。

点 E が線分 OC 上にあることから，$0\leqq t \leqq 1$ である。$-1 < r < 1$ なので，①の右辺の $\cos\theta$ を $r$ に置き換えた分母$\boxed{\text{ ク }}(r+\boxed{\text{ ケ }})$ は正である。したがって，条件 $0 \leqq t \leqq 1$ は

$0 \leqq \boxed{\text{ カ }}(\boxed{\text{ キ }}r+1) \leqq \boxed{\text{ ク }}(r+\boxed{\text{ ケ }})$…②

となる。

$r$ についての不等式②を解くことにより，$\theta$ のとり得る値の範囲は

$\cfrac{\pi}{\boxed{\text{ コ }}}\leqq\theta\leqq\cfrac{\boxed{\text{ サ }}}{\boxed{\text{ シ }}}\pi$

であることがわかる。

(3)　$\cos\theta=-\cfrac{1}{8}$ とする。直線 AE と直線 BD の交点を F とし，三角形 BEF の面積を求めよう。①により，$t=\cfrac{\boxed{\text{ ス }}}{\boxed{\text{ セ }}}$ となり

$\overrightarrow{\text{OF}}=\cfrac{\boxed{\text{ ソ }}}{\boxed{\text{ タ }}}\vec{a}+\cfrac{\boxed{\text{ チ }}}{\boxed{\text{ ツ }}}\vec{c}$

となる。したがって，点 F は線分 AE を $1:\boxed{\text{ テ }}$ に内分する。このことと，平行四辺形 OABC の面積は $\cfrac{\boxed{\text{ トナ }}\sqrt{\boxed{\text{ ニ }}}}{\boxed{\text{ ヌ }}}$ であることから，三角形 BEF の面積は $\cfrac{\boxed{\text{ ネ }}\sqrt{\boxed{\text{ ノ }}}}{\boxed{\text{ ハ }}}$ である。

解答・解説

ア,イ $2,5$　ウエ $20$　オ $0$

カ,キ,ク,ケ $5,2,4,2$　コ $3$

サ,シ $2,3$　ス,セ $1,2$

ソ,タ,チ,ツ $2,3,1,6$　テ $2$

トナ,ニ,ヌ $15,7,2$

ネ,ノ,ハ $5,7,2$

(1)

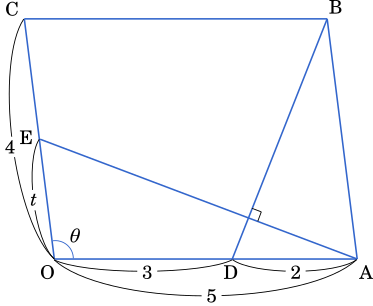
$\overrightarrow{\text{DB}}=\overrightarrow{\text{OB}}-\overrightarrow{\text{OD}}$

$=\vec{a}+\vec{c}-\cfrac{3}{5}\vec{a}$

$=\cfrac{2}{5}\vec{a}+\vec{c}$

また

$\vec{a}\cdot\vec{c}=|5||4|\cos\theta=20\cos\theta$

$\overrightarrow{\text{AE}}\cdot\overrightarrow{\text{DB}}=(t\vec{c}-\vec{a})\bigg(\cfrac{2}{5}\vec{a}+\vec{c}\bigg)$

AE ⊥ DB より $\overrightarrow{\text{AE}}\cdot\overrightarrow{\text{DB}}=0$ だから

$(t\vec{c}-\vec{a})\bigg(\cfrac{2}{5}\vec{a}+\vec{c}\bigg)=0$

$\cfrac{2}{5}t\vec{a}\cdot\vec{c}+t|\vec{c}|^2-\cfrac{2}{5}|\vec{a}|^2-\vec{a}\cdot\vec{c}=0$

$\cfrac{2}{5}t\cdot20\cos\theta+16t-\cfrac{2}{5}\cdot25-20\cos\theta=0$

$8t\cos\theta+16t-10-20\cos\theta=0$

$4t\cos\theta+8t-5-10\cos\theta=0$

$4(\cos\theta+2)t-5(1+2\cos\theta)=0$

$t=\cfrac{5(1+2\cos\theta)}{4(\cos\theta+2)}\cdots$①

(2)

$0\leqq5(2r+1)\leqq4(r+2)\cdots$②

不等式を 2 つに分けるとよい。

$0\leqq5(2r+1)$

$0\leqq2r+1$

$-1\leqq2r$

$-\cfrac{1}{2}\leqq r$

また

$5(2r+1)\leqq4(r+2)$

$10r+5\leqq4r+8$

$6r\leqq3$

$r\leqq\cfrac{1}{2}$

よって

$-\cfrac{1}{2}\leqq r\leqq\cfrac{1}{2}$

$-\cfrac{1}{2}\leqq\cos\theta\leqq\cfrac{1}{2}$

問題文より $0 < \theta < \pi$ に注意して

$\cfrac{\pi}{3}\leqq\theta\leqq\cfrac{2}{3}\pi$

(3)

①に $\cos\theta=-\cfrac{1}{8}$ を代入して

$t=\cfrac{5\bigg(-\cfrac{1}{4}+1\bigg)}{4\bigg(-\cfrac{1}{8}+2\bigg)}=\cfrac{5\cdot\cfrac{3}{4}}{4\cdot\cfrac{15}{8}}$

$=\cfrac{\enspace\cfrac{15}{4}\enspace}{\cfrac{15}{2}}=\cfrac{\enspace\cfrac{1}{4}\enspace}{\cfrac{1}{2}}=\cfrac{2}{4}=\cfrac{1}{2}$

よって，点 E は 線分 OC の中点である。

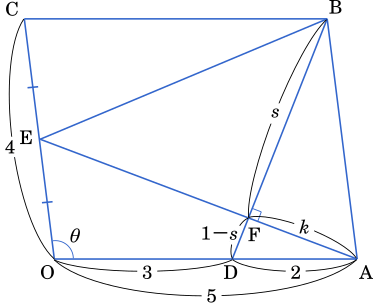
ここから点 A を起点としてベクトルの式を作るとよい。$\overrightarrow{\text{AF}}=k\overrightarrow{\text{AE}}$ とおき，BF : FD = $s:(1-s)$ とすると

$\overrightarrow{\text{AF}}=k\overrightarrow{\text{AE}}$

$=k(\overrightarrow{\text{OE}}-\overrightarrow{\text{OA}})$

$=\cfrac{1}{2}k\vec{c}-k\vec{a}$

また

$\overrightarrow{\text{AF}}=(1-s)\overrightarrow{\text{AB}}+s\overrightarrow{\text{AD}}$

$=(1-s)(\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}})+s(\overrightarrow{\text{OD}}-\overrightarrow{\text{OA}})$

$=(1-s)(\vec{a}+\vec{c}-\vec{a})+s\bigg(\cfrac{3}{5}\vec{a}-\vec{a}\bigg)$

$=(1-s)\vec{c}-\cfrac{2}{5}s\vec{a}$

2 つの式を比べて

$\cfrac{1}{2}k=1-s$

$k=\cfrac{2}{5}s$

これらを連立して

$s=\cfrac{5}{2}k$

$\cfrac{1}{2}k=1-\cfrac{5}{2}k$

$3k=1$

$k=\cfrac{1}{3}$

したがって，点 F は線分 AE を $1:2$ に内分する。

このとき平行四辺形 OABC の面積は 底辺×高さ で求められるが，高さは OC×$\sin\theta$ となる。$\bigg($OC を三角形の斜辺として考えると $\text{OC}\times\sin\theta=\text{斜辺}\times\cfrac{\text{高さ}}{\text{斜辺}}=高さ$ である$\bigg)$。したがって，面積はOA$\times$OC$\times\sin\theta$ となる。

$\sin\theta$ を求めると

$\sin^2\theta+\cos^2\theta=1$

$\sin^2\theta+\bigg(-\cfrac{1}{8}\bigg)^2=1$

$\sin^2\theta+\cfrac{1}{64}=1$

$\sin^2\theta=\cfrac{63}{64}$

$\sin\theta=\cfrac{3\sqrt{7}}{8}$

よって，面積は

$5\times4\times\cfrac{3\sqrt{7}}{8}=\cfrac{15\sqrt{7}}{2}$

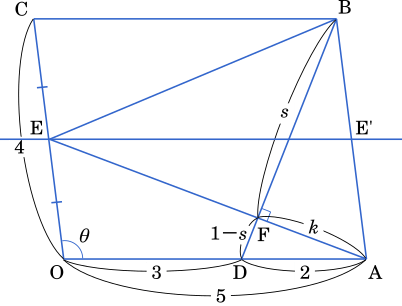
図のように OA に平行な線分 E － E’ を引くと，△BEE’ は平行四辺形 EE’BC の半分，△AE’E は平行四辺形 OAE’E の半分である。よって，△ABE は平行四辺形 OACB の面積の半分であることが分かる。

△ABE = $\cfrac{1}{2}\times\cfrac{15\sqrt{7}}{2}=\cfrac{15\sqrt{7}}{4}$

また，AF : FE = 1 : 2 より

△BEF = $\cfrac{2}{3}\times$△ABE

$=\cfrac{2}{3}\times\cfrac{15\sqrt{7}}{4}$

$=\cfrac{5\sqrt{7}}{2}$