【スマホで読む・わかりやすい】センター数学IIB2019追試【解説・正解・問題】

第4問　解答・解説

ア イ 3 5　ウ エ 3 5
オ,カ,キク 6, 6, －3　ケコ,サ －1, 2
シ 0　ス 2　セ,ソ,タチ 8, 2, －7
ツ 6　テ 6　トナ 85　ニ ヌ 7 6
ネノ,ハ,ヒフ,ヘホ 17, 3, 20, －7

(1)

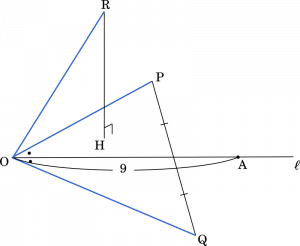
三平方の定理より

$|\overrightarrow{\text{OP}}|=\sqrt{0^2+6^2+3^2}=3\sqrt{5}$

・・・アイ

$|\overrightarrow{\text{OQ}}|=\sqrt{4^2+(^2)^2+(-5)^2}=3\sqrt{5}$

・・・ウエ

よって，△OPQ は二等辺三角形であり，$\ell$ は PQ の中点を通る。

PQ の中点を求めると

$\Big(\cfrac{0+4}{2},\cfrac{6-2}{2},\cfrac{3-5}{2}\Big)$

$=(2,2,-1)$

実数 $k$ を用いて

$\overrightarrow{\text{OA}}=k(2,2,-1)$ とおくと

$|\overrightarrow{\text{OA}}|=\sqrt{(2k)^2+(2k)^2+(-k)^2}=9$

$\sqrt{9k^2}=9$

$3k=9$

$k=3$

したがって

$\overrightarrow{\text{OA}}=(6,6,-3)$

・・・オカキク

(2)

$\vec{n}=(2,y,z)$ とおくと，$\overrightarrow{\text{OP}}$ ⊥ $\vec{n}$ より

$\overrightarrow{\text{OP}}\cdot\vec{n}=0\cdot2+6y+3z=0$

$6y+3z=0$

また，$\overrightarrow{\text{OQ}}$ ⊥ $\vec{n}$ より

$\overrightarrow{\text{OQ}}\cdot\vec{n}=4\cdot2-2y-5z=0$

$2y+5z=8$

式どうしを連立して

$6y+3z=0$

$6y+15z=24$

式を引くと

$-12z=-24$

$z=2$

式に代入して

$6y+3\cdot2=0$

$y=-1$

したがって

$\vec{n}=(2,-1,2)$

・・・ケコサ

$\overrightarrow{\text{OH}}\cdot\vec{n}=0$ だから

・・・シ

$\overrightarrow{\text{OH}}=\overrightarrow{\text{OR}}-k\vec{n}$ より

$\overrightarrow{\text{OH}}\cdot\vec{n}=\overrightarrow{\text{OR}}\cdot\vec{n}-k|\vec{n}|^2$

$0=12\cdot2+0\cdot(-1)+(-3)\cdot2-k\{2^2+(-1)^2+2^2\}$

$18-9k=0$

$k=2$

・・・ス

よって

$\overrightarrow{\text{OH}}=\overrightarrow{\text{OR}}-k\vec{n}$

$=(12,0,-3)-2(2,-1,2)$

$(8,2,-7)$

・・・セソタチ

$\overrightarrow{\text{HR}}=k\vec{n}$ より

$=2(2,-1,2)$

$=(4,-2,4)$

$|\overrightarrow{\text{HR}}|=\sqrt{4^2+(-2)^2+4^2}$

$=6$

・・・ツ

(3)

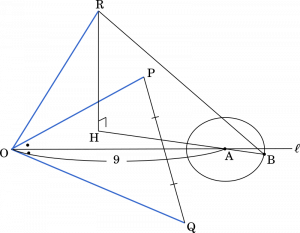
A と H の距離を求めると

$\overrightarrow{\text{AH}}=\overrightarrow{\text{OH}}-\overrightarrow{\text{OA}}$

$=(8,2,-7)-(6,6,-3)$

$=(2,-4,-4)$

$|\overrightarrow{\text{AH}}|=\sqrt{2^2+(-4)^2+(-4)^2}$

$=6$

・・・テ

RB の長さが最大となるとき，HB の長さは最大となる。このとき，H，A，B は一直線上にある。よって

HB = HA ＋ AB ＝ 1 ＋ 6 ＝ 7

三平方の定理を用いて RB の長さを求めると

RB ＝ $\sqrt{7^2+6^2}=\sqrt{85}$

・・・トナ

また

$\overrightarrow{\text{HB}}=\cfrac{7}{6}\overrightarrow{\text{HA}}$

・・・ニヌ

B の座標を求めると

$\overrightarrow{\text{BH}}=\cfrac{7}{6}(2,-4,-4)=\Big(\cfrac{7}{3},-\cfrac{14}{3},-\cfrac{14}{3}\Big)$

$\overrightarrow{\text{BH}}=\overrightarrow{\text{OH}}-\overrightarrow{\text{OB}}$ だから，移行して

$\overrightarrow{\text{OB}}=\overrightarrow{\text{OH}}-\overrightarrow{\text{BH}}$

$=(8,2,-7)-\Big(\cfrac{7}{3},-\cfrac{14}{3},-\cfrac{14}{3}\Big)$

$=\Big(\cfrac{17}{3},\cfrac{20}{3},\cfrac{-7}{3}\Big)$

・・・ネノハヒフヘホ

問題文

点 O を原点とする座標空間に 3 点 P(0，6，3)，Q(4，－2，－5)，R(12，0，－3)がある。3 点 O，P，Q の定める平面を $\alpha$ とし，$\alpha$ 上で ∠POQ の二等分線 $\ell$ を考える。$\ell$ 上に点 A を，$|\overrightarrow{\text{OA}}|$＝ 9 かつ $x$ 座標が正であるようにとる。また，$alpha$ 上に点 H を，$\overrightarrow{\text{HR}}$ ⊥ $\overrightarrow{\text{OP}}$，$\overrightarrow{\text{HR}}$ ⊥ $\overrightarrow{\text{OQ}}$ であるようにとる。

(1) $|\overrightarrow{\text{OP}}|=\boxed{\text{ア}}\sqrt{\boxed{\text{イ}}}$，$|\overrightarrow{\text{OQ}}|=\boxed{\text{ウ}}\sqrt{\boxed{\text{エ}}}$ であるから，A の座標は ($\boxed{\text{オ}}$，$\boxed{\text{カ}}$，$\boxed{\text{キク}}$) であることがわかる。

(2) 点 H の座標と線分 HR の長さを求めよう。$\overrightarrow{\text{OP}}$⊥$\vec{n}$，$\overrightarrow{\text{OQ}}$⊥$\vec{n}$ であるベクトル $\vec{n}=(2，\boxed{\text{ケコ}}$，$\boxed{\text{サ}}$) に対し，$\overrightarrow{\text{HR}}=k\vec{n}$ とおくと $\overrightarrow{\text{OH}}=\overrightarrow{\text{OR}}-k\vec{n}$ である。$\overrightarrow{\text{OH}}\cdot\vec{n}=\boxed{\text{シ}}$ であるから，$k=\boxed{\text{ス}}$ である。したがって，H の座標は($\boxed{\text{セ}}$，$\boxed{\text{ソ}}$，$\boxed{\text{タチ}}$) であり，HR の長さは $\boxed{\text{ツ}}$ である。

(3) 平面 $\alpha$ 上で点 A を中心とする半径 1 の円 $C$ を考える。点 B が $C$ 上を動くとき，線分 RB の長さの最大値と，そのときの B の座標を求めよう。

A と H の間の距離は $\boxed{\text{テ}}$ である。よって，RB の長さの最大値は $\sqrt{\boxed{\text{トナ}}}$ である。また，RB の長さが最大となる B は $\overrightarrow{\text{HB}}=\cfrac{\boxed{\text{ニ}}}{\boxed{\text{ヌ}}}\overrightarrow{\text{HA}}$ を満たすから，求める B の座標は

$\Big(\cfrac{\boxed{\text{ネノ}}}{\boxed{\text{ハ}}}$，$\cfrac{\boxed{\text{ヒフ}}}{\boxed{\text{ハ}}}$，$\cfrac{\boxed{\text{ヘホ}}}{\boxed{\text{ハ}}}\Big)$

である。