楕円と接線(横浜国立大2016理系第5問)

$xy$ 平面上に楕円 $C:\cfrac{x^2}{4}+y^2=1$ がある。次の問いに答えよ。

(1) 点 P$(a,b)$ を通る $C$ の接線が 2 本あり，それらが直交するとき，$a$，$b$ がみたす条件を求めよ。

(2) $C$ に外接する長方形のうち，$x$ 座標が 1 で $y$ 座標が正である頂点をもつものの面積を求めよ。

接線の方程式を求める

(1)から始めます。

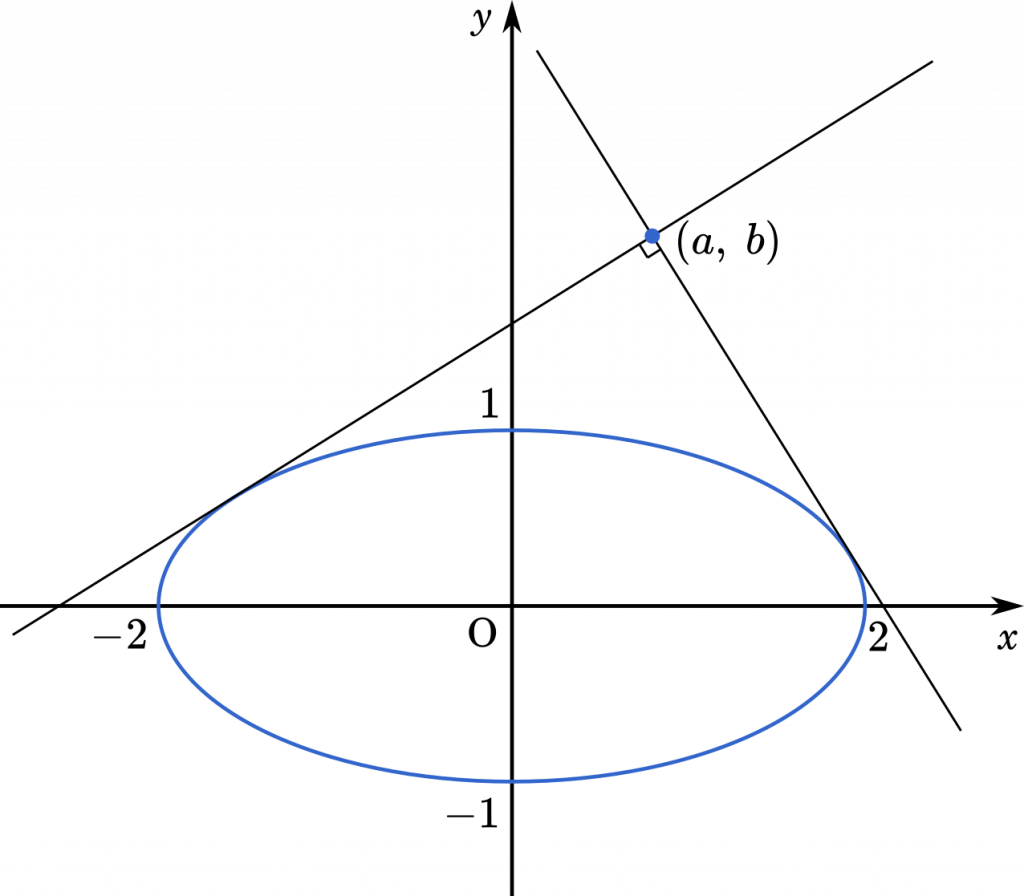
この問題は，楕円の接線を先に作って，それが $(a,b)$ を通る，と考える方法と，$(a,b)$ を通る直線が楕円と 1 か所で接する，と考える方法があります。

実際に式を立ててみると，後者の考えの方が式が作りやすい，という結論になると思います。

$(a,b)$ を通る傾き $k$ の直線の方程式を

$y=k(x-a)+b$　・・・①

とする。

これが楕円と 1 か所で接するので，式を連立して判別式 $D=0$ という条件で考えれば良いでしょう。

①を $\cfrac{x^2}{4}+y^2=1$ に代入すると

$\cfrac{x^2}{4}+\{k(x-a)+b\}^2=1$
$\cfrac{x^2}{4}+k^2(x-a)^2+2bk(x-a)+b^2-1=0$
$\cfrac{x^2}{4}+k^2(x^2-2ax+a^2)+2bkx-2abk+b^2-1=0$
$\cfrac{x^2}{4}+k^2x^2-2ak^2x+a^2k^2+2bkx-2abk+b^2-1=0$

$\Big(\cfrac{1}{4}+k^2\Big)x^2+2k(b-ak)x+a^2k^2-2abk+b^2-1=0$

判別式をつくると

$\cfrac{D}{4}=k^2(b-ak)^2-\Big(\cfrac{1}{4}+k^2\Big)(a^2k^2-2abk+b^2-1)=0$
$k^2(b^2-2abk+a^2k^2)-\cfrac{a^2k^2}{4}+\cfrac{abk}{2}-\cfrac{b^2}{4}+\cfrac{1}{4}-a^2k^4+2abk^3-b^2k^2+k^2=0$
$b^2k^2-2abk^3+a^2k^4-\cfrac{a^2k^2}{4}+\cfrac{abk}{2}-\cfrac{b^2}{4}+\cfrac{1}{4}-a^2k^4+2abk^3-b^2k^2+k^2=0$
$\Big(1-\cfrac{a^2}{4}\Big)k^2+\cfrac{abk}{2}-\cfrac{b^2}{4}+\cfrac{1}{4}=0$

両辺に 4 をかけて

$(4-a^2)k^2+2abk-b^2+1=0$　・・・②

この方程式は $k$ の解が 2 つできますが，接線は 2 本引くことができるので，それぞれの解が接線の傾きを表すことになります。

そして，2 本の直線が直交するとき，傾き同士の積は $-1$ になります。方程式の解を $\alpha,\beta$ とすると，$\alpha\beta=-1$ です。

$\cfrac{-b^2+1}{4-a^2}=-1$
$b^2-1=4-a^2$
$a^2+b^2=5$

この計算では求められないケースがあります。上の図のように直線が垂直($y$軸平行)の場合，傾き $k$ を求めることはできません。しかしこの場合も 2 本の接線は直交し，$a^2+b^2=5$ に座標を代入すると，ちゃんと成り立ちます。解答には

また，式は $(a,b)=(2,1)(2,-1),(-2,1),(-2,-1)$ のときも成立する。

という一文を入れておきましょう。

したがって $a^2+b^2=5$　（答え）

長方形の面積を求める

(2)に進みます。

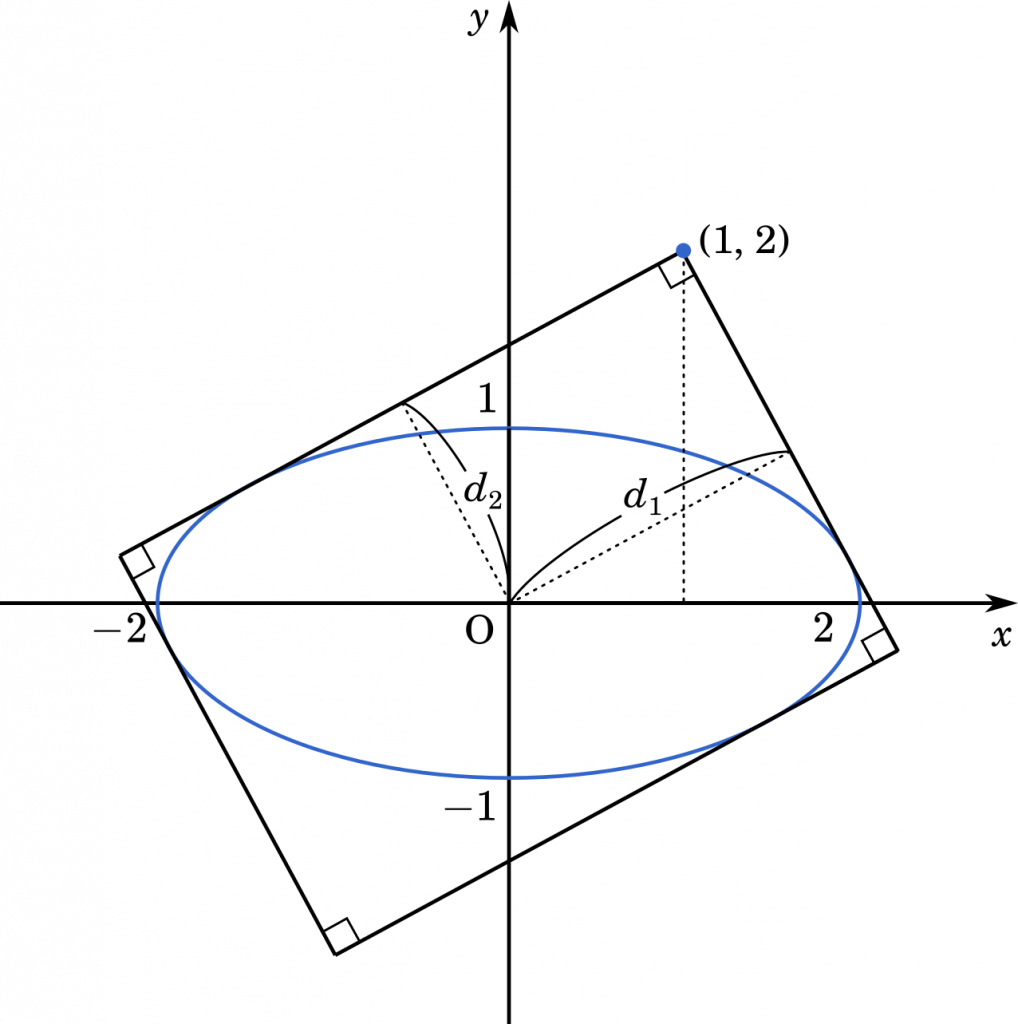
$a^2+b^2=5$ に $a=1$ を代入すると $b=\pm2$ となり，$y$ 座標が正の数のほうなので，$b=2$ となります。

この座標から楕円に向かって接線を引き，長方形をつくります。

長方形の面積は，点と直線の距離の公式を用いて，原点と直線の距離を求めると良いでしょう。

点 $(1,2)$ を通り，楕円に接する直線を

$y=k_1(x-1)+2$

とすると，式を変形して

$k_1x-y+2-k_1=0$

原点と直線の距離は

$d_1=\cfrac{|2-k_1|}{\sqrt{{k_1}^2+1}}$

同様にして

$d_2=\cfrac{|2-k_2|}{\sqrt{{k_2}^2+1}}$

$d_1$ と $d_2$ をそれぞれ 2 倍したものが，長方形のタテとヨコの長さになるので，面積は

$S=\cfrac{4|(2-k_1)(2-k_2)|}{\sqrt{{k_1}^2+1}\sqrt{{k_2}^2+1}}$ $=\cfrac{4|4-2(k_1+k_2)+k_1k_2|}{\sqrt{(k_1k_2)^2+{k_1}^2+{k_2}^2+1}}$

こうなると，$k_1$ と $k_2$ の値を求める必要がでてきますが，(1)で作った式

$(4-a^2)k^2+2abk-b^2+1=0$　・・・②

を利用できそうです。$(a,b)=(1,2)$ を代入すると

$3k^2+4k-3=0$

解と係数の関係より

$k_1+k_2=-\cfrac{4}{3}$
$k_1k_2=-1$

また

${k_1}^2+{k_2}^2=(k_1+k_2)^2-2k_1k_2$ より
$=\cfrac{16}{9}+2=\cfrac{34}{9}$

これらを代入して

$S=\cfrac{4\Big|4+\cfrac{8}{3}-1\Big|}{\sqrt{1+\cfrac{34}{9}+1}}$
$=\cfrac{4\cdot\cfrac{17}{3}}{\sqrt{\cfrac{52}{9}}}$
$=\cfrac{34}{\sqrt{13}}$　（答え）