第二次導関数と変曲点をざっくりおさらい(東京都立大2017理系第1問)

第二次導関数を求める問題やるよ。
微分，二回やるんですよね。でも，何か意味あるんですか？
関数を微分すると接線の傾きが求められるんだけど，同時に関数のある点において，右上がりか右下がりかってのも分かる。
第二次導関数ってのはいわば，変化量の変化量であって，たとえば最初は f′(x)f'(x) が +10+10 だったとしても f”(x)f”(x) がマイナスだと，f′(x)f'(x) が 7,4,1,⋯7,4,1,\cdots みたいにどんどん減っていく。そしてマイナスになったら下り坂に入る。
変曲点ってありますね。
上りと下りが切り替わるところは極値って言うけど，下りでも坂が急からゆるやかに切り替わるところを変曲点って言って，グラフの上に凸と下に凸のさかい目になってる。
第二次導関数を求めると，グラフの形がもう少し詳しく分かるようになる。

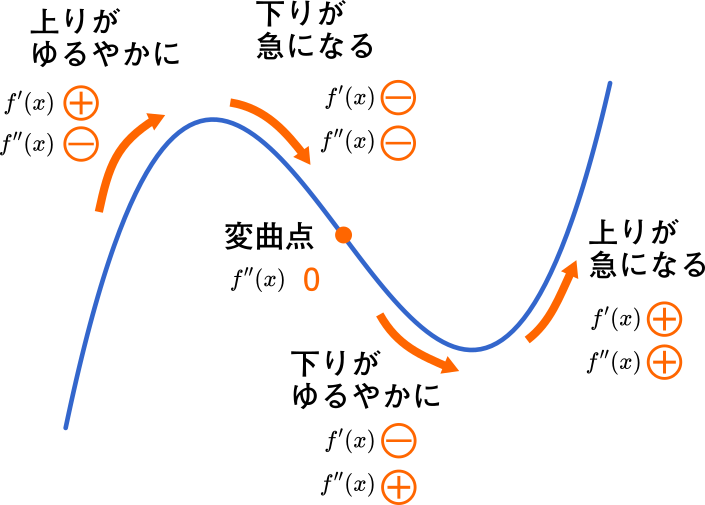
実際の入試問題で第二次導関数を求めてみましょう。

演習問題

nn を自然数とし，ee を自然対数の底とする。関数

f(x)=xn−1e−xf(x)=x^{n-1}e^{-x}

について，以下の問いに答えなさい。（東京都立大2017）

(1) すべての自然数 nn に対して，x≧0x\geqq0 のとき ex>xnn!e^x>\cfrac{x^n}{n!} が成り立つことを，nn に関する数学的帰納法によって示しなさい。

(2) 極限 lim⁡x→∞f(x)\displaystyle\lim_{x\rightarrow\infty}f(x) を求めなさい。

(3) n≧3n\geqq3 の場合に，x>0x>0 の範囲における f(x)f(x) の最大値，およびそのときの xx の値を求めなさい。また，x>0x>0 の範囲における y=f(x)y=f(x) のグラフの変曲点の xx 座標を求めなさい。

グラフが単調増加であることを利用する

(1)から始めます。すべての自然数 nn に対して，という言葉を見たら，まずは数学的帰納法で証明することを考えてみましょう。

x≧0x\geqq0 のとき ex>xnn!e^x>\cfrac{x^n}{n!} ・・・(*)

[I] n=1n=1 のとき

xnn!=x\cfrac{x^n}{n!}=x

不等式を証明するために，(*)の右辺を移項して式が 0 以上になることを証明します。

g(x)=ex−xg(x)=e^x-x として

g′(x)=ex−1g'(x)=e^x-1

増減表は

 x0⋯ g′(x)0+ g(x)1↗\def\arraystretch{1.5}\begin{array}{|c|c|c|}\hline x&0&\cdots\\\hline g'(x)&0&+\\\hline g(x)&1&\nearrow\\\hline\end{array}

x≧0x\geqq0 のとき，g(x)g(x) は単調増加であるから，g(x)>0g(x)>0 が成り立つ。

よって，ex>xe^x>x が成り立つ。

[II] n=kn=k のとき，(*)が成り立つと仮定して，n=k+1n=k+1 とすると

h(x)=ex−xk+1(k+1)!h(x)=e^x-\cfrac{x^{k+1}}{(k+1)!}
h′(x)=ex−(k+1)xk(k+1)!h'(x)=e^x-\cfrac{(k+1)x^k}{(k+1)!}

(k+1)!=1⋅2⋯ k⋅(k+1)(k+1)!=1\cdot2\cdots k\cdot(k+1) より

(k+1)!=k!(k+1)(k+1)!=k!(k+1) となるので

h′(x)=ex−(k+1)xkk!(k+1)h'(x)=e^x-\cfrac{(k+1)x^k}{k!(k+1)}
=ex−xkk!>0=e^x-\cfrac{x^k}{k!}>0

よって，n=k+1n=k+1 のときも(*)が成り立つ。

[I]，[II]より，x≧0x\geqq0 のとき，すべての自然数 nn に対して，ex>xnn!e^x>\cfrac{x^n}{n!} が成り立つ。（証明終わり）

はさみうちの原理

(2)に進みます。

(1)の不等式を使って，f(x)f(x) の形に合わせていきます。

ex>xnn!e^x>\cfrac{x^n}{n!}
1ex<n!xn\cfrac{1}{e^x}<\cfrac{n!}{x^n}

2<32<3 → 12>13\cfrac{1}{2}>\cfrac{1}{3} みたいにして，逆数とると不等号の向きが変わるので注意。

0<e−x<n!xn0<e^{-x}<\cfrac{n!}{x^n}

ee を何乗してもマイナスになることはないから，常に正の値。

0<xn−1e−x<xn−1n!xn0<x^{n-1}e^{-x}<\cfrac{x^{n-1}n!}{x^n}
0<xn−1e−x<n!x0<x^{n-1}e^{-x}<\cfrac{n!}{x}

はさみうちの原理より

lim⁡x→∞0<lim⁡x→∞xn−1e−x<lim⁡x→∞n!x\displaystyle\lim_{x\rightarrow\infty}0<\lim_{x\rightarrow\infty}x^{n-1}e^{-x}<\lim_{x\rightarrow\infty}\cfrac{n!}{x}
0<lim⁡x→∞xn−1e−x<0\displaystyle0<\lim_{x\rightarrow\infty}x^{n-1}e^{-x}<0

したがって

lim⁡x→∞f(x)=0\displaystyle\lim_{x\rightarrow\infty}f(x)=0

（証明終わり）

第二次導関数を求める

(3)に進みます。変曲点が必要なので，第二次導関数，つまり二回目の微分を求めます。

f(x)=xn−1e−xf(x)=x^{n-1}e^{-x}　(n≧3,  x>0)(n\geqq3,\space x>0)
f′(x)=(xn−1)’e−x+xn−1(e−x)’f'(x)=(x^{n-1})’e^{-x}+x^{n-1}(e^{-x})’
=(n−1)xn−2e−x−xn−1e−x=(n-1)x^{n-2}e^{-x}-x^{n-1}e^{-x}
=xn−2e−x(n−1−x)=x^{n-2}e^{-x}(n-1-x)

ここは，xn−2× x=xn−1x^{n-2}\times x=x^{n-1} ってななるから，1 個上に戻るのを確認して。

ここで，いったん極値を求めておきます。

xn−2e−x(n−1−x)=0x^{n-2}e^{-x}(n-1-x)=0 とすると

x>0x>0 より xn−2e−x≠0x^{n-2}e^{-x}\not=0 だから

n−1−x=0n-1-x=0
x=n−1x=n-1

 x(0)⋯n−1⋯ f′(x)+0− f(x)↗↘\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|}\hline x&(0)&\cdots&n-1&\cdots\\\hline f'(x)&&+&0&-\\\hline f(x)&&\nearrow&&\searrow\\\hline\end{array}

最大値は

f(n−1)=(n−1)n−1e−(n−1)f(n-1)=(n-1)^{n-1}e^{-(n-1)}
=(n−1)n−1⋅1en−1=(n-1)^{n-1}\cdot\cfrac{1}{e^{n-1}}
=(n−1e)n−1=\Big(\cfrac{n-1}{e}\Big)^{n-1}

さらに微分します。

f”(x)=(xn−2e−x)′(n−1−x)+(nn−2e−x)(n−1−x)’f”(x)=(x^{n-2}e^{-x})'(n-1-x)+(n^{n-2}e^{-x})(n-1-x)’
={(xn−2)’e−x+xn−2(e−x)’}(n−1−x)−xn−2e−x=\{(x^{n-2})’e^{-x}+x^{n-2}(e^{-x})’\}(n-1-x)-x^{n-2}e^{-x}
={(n−2)xn−3e−x−xn−2e−x}(n−1−x)−xn−2e−x=\{(n-2)x^{n-3}e^{-x}-x^{n-2}e^{-x}\}(n-1-x)-x^{n-2}e^{-x}
=xn−3e−x{(n−2−x)(n−1−x)−x}=x^{n-3}e^{-x}\{(n-2-x)(n-1-x)-x\}

ここも，xn−3× x=xn−2x^{n-3}\times x=x^{n-2} の関係。

=xn−3e−x{(n−1)(n−2)−(n−2+n−1)x+x2−x}=x^{n-3}e^{-x}\{(n-1)(n-2)-(n-2+n-1)x+x^2-x\}
=xn−3e−x{(n−1)(n−2)−2(n−1)x+x2}=x^{n-3}e^{-x}\{(n-1)(n-2)-2(n-1)x+x^2\}

変曲点を求めます。

xn−3e−x{(n−1)(n−2)−2(n−1)x+x2}=0x^{n-3}e^{-x}\{(n-1)(n-2)-2(n-1)x+x^2\}=0 とすると

xn−3e−x≠0x^{n-3}e^{-x}\not=0 だから
x2−2(n−1)x+(n−1)(n−2)=0x^2-2(n-1)x+(n-1)(n-2)=0

二次方程式の解の公式より

x=n−1±(n−1)2−(n−1)(n−2)x=n-1\pm\sqrt{(n-1)^2-(n-1)(n-2)}
=n−1±n2−2n+1−n2+3n−2=n-1\pm\sqrt{n^2-2n+1-n^2+3n-2}
=n−1±n−1=n-1\pm\sqrt{n-1}

変曲点が求められました。

したがって

最大値は (n−1e)n−1\Big(\cfrac{n-1}{e}\Big)^{n-1}
変曲点は n−1±n−1n-1\pm\sqrt{n-1}　（答え）

SNSでシェア

mm参考書 2019-2023