【数Ⅲ積分】円柱を斜めに切った立体の体積を求める

三角形の面積の積分で求める

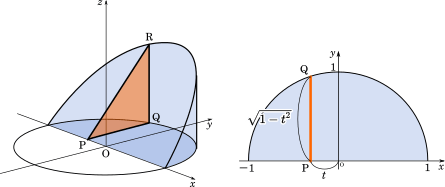
この立体の体積は、三角形の面積を積み上げた形として考えましょう。三角形の面積を積分すると体積になります。

ここで、三角形を △PQR として面積を求めてみます。$45\text°$ で切断しているので、この三角形は底辺と高さが等しい直角二等辺三角形です。

まず、点P の座標を$(t,0)$として、そこから 点Q の座標を考えます。

点Q は円周上にあります。この円の方程式は $x^2+y^2=1$ です。これを変形すると、$y=\sqrt{1-x^2}$ となります。よって、点Q の座標は $(t, \sqrt{1-t^2})$ です。

そして、△PQR は直角二等辺三角形なので、$PQ=QR=\sqrt{1-t^2}$ となり、△PQR の面積はこうなります。

△PQR = $\displaystyle\frac{1}{2}(1-t^2)$

これを積分で積み上げていきましょう。$t$ は$-1$ から $1$ まで変化していくので、求める体積の式はこうなります。

$\displaystyle\int_{-1}^{1} \frac{1}{2}(1-t^2)\enspace dt$

今回の立体は左右対称の形をしています。そこで、積分区間を半分にして、その結果を２倍しても同じことになります。

では、計算していきましょう。

$\displaystyle 2\int_{0}^{1}\frac{1}{2}(1-t^2)\enspace dt=\int_{0}^{1}1-t^2\enspace dt$
$=\displaystyle\left[ t-\frac{t^3}{3}\right]_0^1=1-\frac{1}{3}=\frac{2}{3}$　（答え）

大事なのは 点Q の座標の求め方です。実際に図を描いてみることで 点Q がどうなるのかを確認して座標を求めましょう。

長方形の面積の積分で求める

今度は長方形の面積を積み上げるパターンで考えてみましょう。

ここで、点Q の座標を求めて考えましょう。今度は 長方形を $y$ 軸方向で積み上げていくので、点Q の $y$ 座標を$t$ とします。

$x^2+y^2=1$ を変形して、$x=\sqrt{1-y^2}$ とします。

よって、$y=t$ とすれば、点Q の座標は $(\sqrt{1-t^2},t)$ です。また、$45\text°$ で切断しているので、$x$ 軸から PQ までの距離が長方形の高さと等しくなります。よって、QR=$t$ です。

また、PQ の長さは $2\sqrt{1-t^2}$ となるので、長方形PQRSの面積は $2t\sqrt{1-t^2}$ となります。

$t$ は $0$ から $1$ まで変化していくので、体積の式はこうなります。

$\displaystyle\int_0^1 2t\sqrt{1-t^2}\enspace dt$

計算していきましょう。

$\displaystyle =2\int_0^1 t\sqrt{1-t^2}\enspace dt$

ここで、置換積分をします。$\sqrt{1-t^2}=u$ として

$1-t^2=u^2\\-2t\enspace dt=2u\enspace du\\t\enspace dt=-u\enspace du$

$t\enspace 0\rightarrow 1\\u\enspace 1 \rightarrow 0$ となるので

$\displaystyle\int_1^0{-2u\cdot u\enspace du}=-2\int_1^0 u^2\enspace du$
$\displaystyle=-2\left[ \frac{u^3}{3}\right]_1^0=-2\left\{0-\frac{1}{3}\right\}$
$\displaystyle=\frac{2}{3}$　(答え)

円柱の半径が２になる場合

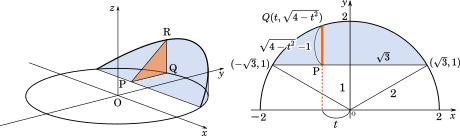
順番に整理していきましょう。

今回は 点Q は半径２の円周上です。円の方程式は $x^2+y^2=4$ です。これを変形して

$y=\sqrt{4-x^2}$

となります。

そして、点Q の $x$ 座標を $t$ とすると、Q$(t,\sqrt{4-t^2})$ です。

また、今回は $y=1$ の直線からの距離なので、PQ = $\sqrt{4-t^2}-1$ です。

ここから △PQR の面積を求めましょう。

今回も斜め 45°で切断しているので、三角形の底辺と高さは同じです。よって、

△PQR = $\displaystyle\frac{1}{2}(\sqrt{4-t^2}-1)^2$

次に積分区間を考えます。

図にあるように、$y=1$ の直線と半径を結ぶと、$1:2:\sqrt{3}$ の三角形ができます。

そこから、積分区間は $-\sqrt{3}$ から $\sqrt{3}$ であることが分かります。

よって求める体積は

$\displaystyle\int_{-\sqrt{3}}^{\sqrt{3}} \frac{1}{2}(\sqrt{4-t^2}-1)^2\enspace dt$

ここで、上の問題と同じようにこの立体も左右対称なので積分区間を半分にして２倍しましょう。

$\displaystyle =\int_{0}^{\sqrt{3}}(\sqrt{4-t^2}-1)^2\enspace dt$

これを展開すると

$\displaystyle =\int_{0}^{\sqrt{3}}4-t^2-2\sqrt{4-t^2}+1\enspace dt$
$\displaystyle =\int_{0}^{\sqrt{3}} 5-t^2-2\sqrt{4-t^2}\enspace dt$

式が長いので２つに分けて計算しましょう。

$\displaystyle\int_{0}^{\sqrt{3}} 5-t^2\enspace dt$
$=\displaystyle\left[ 5t-\frac{t^3}{3}\right]_0^{\sqrt{3}}$
$=5\sqrt{3}-\sqrt{3}=4\sqrt{3}\cdots\text①$

また

$\displaystyle\int_0^{\sqrt{3}} -2\sqrt{4-t^2}\enspace dt$
$=\displaystyle -2\int_0^{\sqrt{3}} \sqrt{4-t^2}\enspace dt$

ここで、置換積分に持ち込みます。$t=2\sin{u}$ とします。

置換積分の応用：$\sqrt{4-t^2}$ を置換積分で求める

置換を行うのは、ルートが邪魔でそれをはずしたいからです。$1-\sin^2{t}=\cos^2{t}$ の関係を使って $\sqrt{1-\sin^2{t}}=\cos{t}$ としたいから $\sin{}$ で置換するのです。

ところが今回は $\sqrt{4-t^2}$ となっていて、１ではなく４です。そこで、$t=2\sin{u}$ とすると、$\sqrt{4-4\sin^2{u}}$ となり、係数を外に追い出して $2\sqrt{1-\sin^2{u}}$ とすることができるのです。

さらに半角の公式に持ち込む

問題に戻りましょう。

$t=2\sin{u}$ として

$\displaystyle\frac{dt}{du}=2\cos{u}$
$dt=2\cos{u}\enspace du$

ここで、$t\enspace0\rightarrow \sqrt{3}$、$\displaystyle u\enspace0\rightarrow\frac{\pi}{3}$ となるので

$\displaystyle -2\int_0^{\frac{\pi}{3}} \sqrt{4-4\sin^2{u}}\cdot2\cos{u}\enspace du$
$\displaystyle=-2\int_0^{\frac{\pi}{3}} 2\sqrt{1-\sin^2{u}}\cdot2\cos{u}\enspace du$
$\displaystyle=-8\int_0^{\frac{\pi}{3}} \cos^2{u}\enspace du$

ここで、半角の公式を使います。sin や cos で二乗の形が出てきたら半角の公式を使うことを考えましょう。

$\displaystyle =-8\int_0^{\frac{\pi}{3}} \frac{1+\cos{2u}}{2}\enspace du$
$\displaystyle=-4\int_0^{\frac{\pi}{3}} 1+\cos{2u}\enspace du$
$\displaystyle=\left[t+\sin{2u}\cdot\frac{1}{2}\right]_0^{\frac{\pi}{3}}$
$\displaystyle=-4\left(\frac{\pi}{3}+\frac{\sqrt{3}}{2}\cdot\frac{1}{2}\right)$
$\displaystyle=-\frac{4}{3}\pi-\sqrt{3}\cdots\text②$

①＋②より

$\displaystyle4\sqrt{3}-\frac{4}{3}\pi-\sqrt{3}$
$\displaystyle=3\sqrt{3}-\frac{4}{3}\pi$

(答え)

実際に図を描いて面積を考えることがポイント

体積を求める積分の計算では、実際に図を描いて面積の式を作ることが大切です。図に座標を書き込んで底辺や高さなどの値を具体的にイメージできるように練習していきましょう。