東京都立大2019理系第１問【複素数平面】複素数全体が円・垂直二等分線になる（教科書レベルから復習しつつ入試問題）

$\alpha=-4-2i,\beta=2+i$ とする。ただし、$i$ は虚数単位を表す。複素数平面上において $|z-\alpha|=2|z-\beta| $をみたす点 $z$ の集合を $C$ とする。以下の問いに答えなさい。（首都大学東京2019)

(1) $C$ は複素数平面上の円になることを示し、その円の中心と半径を求めなさい。
(2) 点 $z$ が $z=0$ を除いて $C$ 上を動くとき、$\displaystyle w=\frac{1}{z}$ で定まる点 $w$ が複素数平面上で直線を描くことを示しなさい。
(3) 複素数平面上の $2$ 点 $A(\alpha)$ と $B(\beta)$ を通る直線を $l$ とし、(2)で示した $w$ の描く直線を $m$ とする。$l$ と $m$ が $1$ 点で交わることを示し、$l$ と $m$ のなす角 $\displaystyle \theta\left(0<0\leqq\frac{\pi}{2}\right)$ について $\cos \theta$ の値を求めなさい。

ここでやるのは円の作りかた、垂直二等分線の作り方、複素数の割り算、複素数から極形式への変換。基本通りだけど少しアイデアが必要な部分もあるから実践で身につけてね。

円に持ち込む

複素数 $z$ 全体が円を表すとき　$|z-$中心$|=$半径
最終的にこの形に持ち込むわけか。

$\alpha$ と $\beta$ を比べて 2 倍の関係が見えると計算ラクになるよ。

$\alpha=-2\beta$
$\displaystyle\beta=-\frac{\alpha}{2}$
与式に代入すると
$\displaystyle|z-\alpha|=2\left|z+\frac{\alpha}{2}\right|$
絶対値がジャマで何もできない。

こういうときは公式 $z\bar z=|z|^2$ を使って絶対値をはずす。

両辺を2乗して
$\displaystyle|z-\alpha|^2=4\left|z+\frac{\alpha}{2}\right|^2$
$\displaystyle (z-\alpha)(\bar z-\bar \alpha)=4\left(z+\frac{\alpha}{2}\right)\left(\bar z+\frac{\bar\alpha}{2}\right)$
$z\bar z-\bar \alpha z-\alpha\bar z+\alpha\bar\alpha=4z\bar z+2\bar\alpha z+2\alpha\bar z+\alpha\bar\alpha$
$3z\bar z+3\bar\alpha z+3\alpha\bar z=0$
$z\bar z+\bar\alpha z+\alpha\bar z=0$

ここから因数分解します。
$(z+a)(\bar z+b)=z\bar z+bz+a\bar z+ab$ の関係を逆向きに考えて、$a$ に $\alpha$、$b$ に $\bar\alpha$ を当てはめるとうまくいきそうです。そして、展開したとき $ab$ の部分が余計なので引き算をしてつじつま合わせをしましょう。

$$z\bar z+bz+a\bar z=(z+a)(\bar z+b)-ab$$

$(z+\alpha)(\bar z+\bar\alpha)-\alpha\bar\alpha=0$
$(z+\alpha)(\overline{z+\alpha})=|\alpha|^2$
$|z+\alpha|^2=|\alpha|^2$
$|z+\alpha|=|\alpha|$
ここで $|\alpha|$ を求める。

複素数平面で絶対値は長さのことだから、三平方の定理を使って長さを求める。

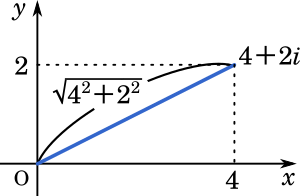
$|\alpha|=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}$
よって
$|z+\alpha|=2\sqrt{5}$
$|z-4-2i|=2\sqrt{5}$
中心 $4+2i$、半径 $2\sqrt{5}$ の円　（答え）

$w$ の式に変形する

(2) に進みます。

直線であるってのを示す一つの方法は垂直二等分線。
$z$ 全体が点$P$、点$Q$の垂直二等分線であるとき　$|z-$点$P|=|z-$点$Q|$

$\displaystyle w=\frac{1}{z}$ より $\displaystyle z=\frac{1}{w}$
(1) で求めた式に代入して
$\displaystyle \left|\frac{1}{w}-4-2i\right|=2\sqrt{5}$
両辺に $|w|$ をかけて
$|1-(4+2i)w|=2\sqrt{5}|w|$
$|(4+2i)w-1|=2\sqrt{5}|w|$

左辺の引き算ってひっくり返して大丈夫なの？

大丈夫。たとえば $|1-3|=|-2|=2$ で $|3-1|=|2|=2$ みたいに絶対値付けると結局どっちも一緒になるでしょ？

両辺を $|4+2i|$ でわると
$\displaystyle \left|w-\frac{1}{4+2i}\right|=\frac{2\sqrt{5}|w|}{|4+2i|}$
ここで $|4+2i|=\sqrt{4^2+2^2}=2\sqrt{5}$ であることに注意すると
$\displaystyle \left|w-\frac{1}{4+2i}\right|=|w|$
また、$\displaystyle \frac{1}{4+2i}$ は有理化して
$\displaystyle \frac{1}{4+2i}=\frac{2-i}{10}$
$\displaystyle \left|w-\frac{2-i}{10}\right|=|w|$
したがって、$w$ は 点$P(0)$、点$\displaystyle Q\left(\frac{2-i}{10}\right)$ の垂直二等分線である。（答え）

直線を$k$ 倍して伸ばす

(3) に進みます。

まずは、$l$ と $m$ が 1 点で交わることを示します。平面上に直線が 2 本あればどこか一か所で交わるのは当然のような気もしますが一応示していきましょう。

示しかたとしては、点$A$ と点$B$ を結ぶ直線を $k$倍して伸ばした直線が $w$ にぶつかることを利用します。

（証明）

$l$ と $m$ が 1 点で交わるとき、$w=\alpha+k(\alpha-\beta)$ となる実数 $k$ が 1 つだけ存在する。
$\alpha=-2\beta$ より $\beta-\alpha=3\beta$
$w=-2\beta+3k\beta=(3k-2)\beta$
$\bar w=(3k-2)\bar \beta$
また $\bar \beta=2-i$ である
これを (2) で求めた式に代入すると
$\displaystyle \left|w-\frac{\bar\beta}{10}\right|=|w|$
公式 $z\bar z=|z|^2$ より
$\displaystyle \left(w-\frac{\bar\beta}{10}\right)\left(\bar w-\frac{\beta}{10}\right)=w\bar w$
$\displaystyle w\bar w-\frac{\beta w}{10}-\frac{\bar \beta\bar w}{10}+\frac{\beta\bar\beta}{100}=w\bar w$
$\beta\bar\beta=(2+i)(2-i)=5$ より
$\displaystyle -\frac{\beta w}{10}-\frac{\bar\beta\bar w}{10}+\frac{1}{20}=0$
$2\beta w+2\bar\beta\bar w=1$
$2(3k-2)\beta^2+2(3k-2)\bar\beta^2=1$
$2(3k-2)(\beta^2+\bar\beta^2)=1$
$12(3k-2)=1$
$\displaystyle 3k-2=\frac{1}{12}$
$\displaystyle k=\frac{25}{36}$
したがって、$k$ は 1 つの実数に定まり、$l$ と $m$ は 1 点で交わる。（証明終了）

複素数を極形式で表す

つぎに $\cos\theta$ を求めます。

複素数平面で $\cos\theta$ が出てくる形は、極形式でした。

複素数の極形式　$r(\cos\theta+i\sin\theta)$　($r$：長さ、$\theta$：偏角）

ここで $w$ の描く直線 $m$ を表す方法を考えなければなりませんが、このままではうまく表すことができません。そこで(2)で求めた垂直二等分線の式より、点$\displaystyle C\left(\frac{1}{\alpha}\right)$、点$\displaystyle D\left(-\frac{2}{\alpha}\right)$ とすると、直線 $CD$ は 直線$m$ と垂直であることから、直線 $CD$ を $90\degree$ 回転してみると良さそうです。
どうやって回転するの？
詳しくは教科書で複素数の回転のところを復習すべきだけど、手っ取り早く言うと $i$ をかけると $90\degree$ 回転する。

直線 $CD$ を $90\degree$ 回転させると
$\displaystyle \left\{\frac{1}{\alpha}-\left(-\frac{2}{\alpha}\right)\right\}i=\frac{3i}{\alpha}$
（原点と始点とする直線 $m$ と平行な直線）
また
$\displaystyle \alpha-\beta=\alpha+\frac{\alpha}{2}=\frac{3\alpha}{2}$
（原点を始点とする直線 $l$ と平行な直線）

ここで複素数の極形式と割り算の関係を思い出しましょう。

複素数の割り算
$z_1=r_1(\cos\theta_1+i\sin\theta_1)$
$z_2=r_2(\cos\theta_2+i\sin\theta_2)$
のとき
$\displaystyle \frac{z_1}{z_2}=\frac{r_1}{r_2}\{\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\}$

割り算をするとき偏角同士は引き算となり、2つの直線のなす角を求めることができます。

よって、割り算をしていきましょう。

どっちをどっちで割るの？

今回は条件 $\left(0<\theta\leqq\frac{\pi}{2}\right)$ だから、$\cos\theta$ の値が正の数であればよい。もしマイナスになったら計算やりなおすのが素直だろうね。

$\displaystyle \frac{\frac{3i}{\alpha}}{\frac{3\alpha}{2}}=\frac{\frac{i}{\alpha}}{\frac{\alpha}{2}}=\frac{i}{\frac{\alpha^2}{2}}=\frac{2i}{\alpha^2}$
$\alpha=-4-2i$ を代入して
$\displaystyle \frac{2i}{(-4-2i)^2}=\frac{2i}{12+16i}=\frac{i}{6+8i}$
分母に $i$ があるので有理化します。
$\displaystyle =\frac{i(6-8i)}{(6+8i)(6-8i)}=\frac{8+6i}{36+64}$
$\displaystyle =\frac{8+6i}{100}=\frac{4+3i}{50}$
ここから極形式に持ち込みます。

$z=r(\cos\theta+i\sin\theta)$ の形から考えると実部が横方向、虚部が縦方向だと言えるよね。つまり、３：４：５の直角三角形になるってこと。

$\cos$ は $\displaystyle\frac{\text{底辺}}{\text{斜辺}}$、$\sin$ は $\displaystyle\frac{\text{高さ}}{\text{斜辺}}$ で表します。それに式を合わせると
$\displaystyle =\frac{1}{10}(\frac{4}{5}+\frac{3}{5}i)$

$\cos$ と $\sin$ の両方で三角比のつじつまが合ってないとダメよ。だからここは分母が $5$ になる。

あとは $z=r(\cos\theta+i\sin\theta)$ の形から考えて $\displaystyle cos\theta=\frac{4}{5}$ となります。これは、$\left(0<\theta\leqq\frac{\pi}{2}\right)$ の条件に合う。したがって
$\displaystyle cos\theta=\frac{4}{5}$　（答え）

SNSでシェア

mm参考書 2019-2023