【数Ⅲ】複素数平面って結局、何？　目に見えない異世界へのアプローチ

ドラえもんの二次元ポケット

数直線を考えてみましょう。数直線は線が１本で出来ています。

ところでこの数直線上で複素数 $1+i$ を示す点はどこにあるでしょうか？おそらく、いくら考えてもこの数直線上で $1+i$ の点を示すことはできないでしょう。小学生のころからお馴染みの数直線ですが、実は数直線で示すことができるのは実数だけということが分かります。

現実の私たちが住む世界は縦・横・奥行の３つの軸で構成されています。いわゆる３Dの世界ということです。一方で数直線は軸が一つしかないので一次元の世界であると言えます。一次元の世界は前に進むか後ろに戻るかしかない、トンネルの中のようなとても窮屈な世界です。

そこで、数直線が実数しか表せないなら虚数を表す軸を加えてみましょう。軸が増えることで直線が平面になりました。これが複素数平面です。とは言え虚軸方向に広がる平面は現実の世界ではなく、あくまで想像上の世界です。

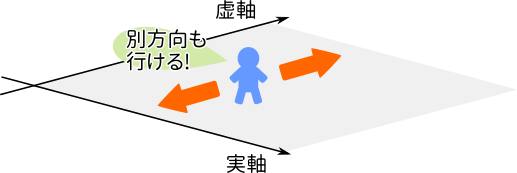
見えないはずのものを見える化する

こうして実際には存在しないはずの複素数を平面上の点として表すと、複素数の様々な計算がグラフ上で表現できることが分かりました。複素数同士のかけ算はグラフ上では回転を表す、と言うのもその一つです。

絶対値＝長さの見える化

数直線に戻って今度は絶対値について考えましょう。数としてはマイナスの数からマイナス符号をとったものが絶対値だという言い方もできますが、これをグラフ上で説明するとしたらどうしますか？

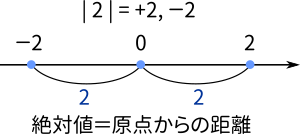
説明は上のようになります。絶対値はグラフ上では原点からの距離に一致します。

そこで数直線に虚軸を加えて平面になったらどうなるでしょうか。

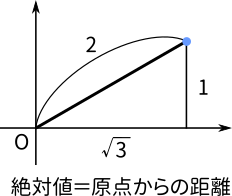
数直線と同じルールを適用することで、平面上でも絶対値が定義できました。

二次方程式の虚数解を見える化する

今度は二次方程式の虚数解をグラフ上に示してみましょう。

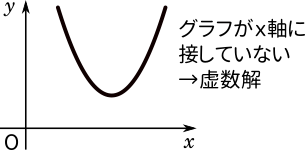
例えば、$x^2-4x+5=0$ の解は、公式を使って $x=2\pm i$ となります。$x^2-4x+5$ は平方完成すると $(x-2)^2+1$ となり、頂点が $(2,1)$ となるので、$x$ 軸と接することはありません。このようにグラフが $x$ 軸に接していないときに虚数解になるのでした。

この虚数解をグラフで表すとしたらどのようにすれば良いでしょうか？

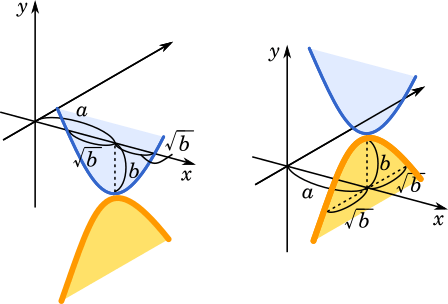
二次関数 $(x-a)^2+b=0$ を考えてみます。これの解を求めると $b<0$ のとき

$(x-a)^2+b=0\\y=x^2-2ax+a^2+b=0\\\displaystyle x=\frac{2a\pm\sqrt{4a^2-4(a^2+b)}}{2}\\x=a\pm\sqrt{b}$

となります。これはグラフで表すと左の図です。

ここに、青のグラフを上下反転して90度回転させたグラフを青のグラフの下に書きます。オレンジのグラフです。

そして $b>0$のとき、方程式の解は $x=a\pm\sqrt{b}i$ となります。これは右のグラフで表されます。オレンジのグラフが$x$軸と虚軸で作られた複素数平面と交わる点が方程式の解です。こうして、複素数平面上に二次方程式の虚数解を示すことができました。

ここで今回の話は終わりです。目に見えないものを考えるという作業はいくら追求してもすっきりしないものかもしれません。しかし、マクロな宇宙の世界やミクロな原子の世界など、私たちの手の届かない世界はいくらでもあります。私たちは複素数の世界を学ぶことでそうした手の届かない世界にアプローチするためのテクニックの一部を学んでいるのです。