【数Ⅲ複素数平面】αβの方程式、直線のなす角を求める
$s>0,t>0$ とする。原点をOとする複素数平面において、$\alpha=2-i,\beta=s+ti$ を表す点をそれぞれA、Bとする。さらに、点Cを直線OBに関して点Aと反対側にとり、△OBCが正三角形になるようにする。点Cを表す複素数を $z$ とするとき、以下の問いに答えよ。(熊本大・改)
(1) $z$ を $s,t$ を用いて表せ。
(2) $\alpha,\beta$ が等式 $4\alpha^2+\beta^2-2\alpha\beta=0$ を満たすとき、$\displaystyle\frac{\beta}{\alpha}$と∠AOBをそれぞれ求めよ。また、$\beta$ と $z$ をそれぞれ求めよ。

問題集でやった練習通りでいけるヤツではあるけど、(2)の方程式の解き方と割り算から角度求めるところを実際の入試問題で腕試ししてみてね。
複素数平面における回転
まずはグラフを描いてみるとこのようになります。
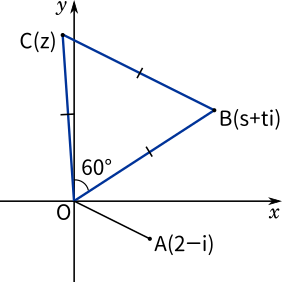
△OBC が正三角形であることに注意して、点Bを$\displaystyle\frac{\pi}{3}$ 回転させれば点Cになります。

複素数平面ではかけ算をすれば回転になるんだった。
$\displaystyle z=(s+ti)\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)\\\displaystyle=(s+ti)\left(\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\\displaystyle=\frac{s}{2}+\frac{\sqrt{3}}{2}si+\frac{t}{2}i-\frac{\sqrt{3}}{2}t\\\displaystyle=\frac{s}{2}-\frac{\sqrt{3}}{2}t+\left(\frac{\sqrt{3}}{2}s+\frac{t}{2}\right)i$
(答え)
αβの方程式を解く
(2)では $4\alpha^2+\beta^2-2\alpha\beta=0$ を $\displaystyle\frac{\beta}{\alpha}$ の式に変形して解きます。

両辺を $\alpha^2$ で割ると良い。
$\displaystyle 4+\frac{\beta^2}{\alpha^2}-2\frac{\beta}{\alpha}=0\\\displaystyle\frac{\beta^2}{\alpha^2}-2\frac{\beta}{\alpha}+4=0$
ここで $\displaystyle\frac{\beta}{\alpha}=A$ として
$\displaystyle A^2-2A+4=0\\A=1\pm\sqrt{1-4}=1\pm\sqrt{3}i$
よって $\displaystyle\frac{\beta}{\alpha}=1\pm\sqrt{3}i$

$\alpha\beta$ の方程式がきたら $\displaystyle\frac{\beta}{\alpha}$ の形に持っていくは一応セオリー。さらにここから極形式に持っていく。
$\displaystyle\frac{\beta}{\alpha}=2\left(\frac{1}{2}\pm\frac{\sqrt{3}}{2}i\right)\\\displaystyle=2\left(\cos\frac{\pi}{3}\pm i\sin\frac{\pi}{3}\right)$
よって∠AOB=$\displaystyle\frac{\pi}{3}$

これは言いかえると、$\alpha$ を長さ2倍して $\displaystyle+\frac{\pi}{3}$ 回転させると $\beta$ になるということ。グラフ上の位置関係からして $-$ ではないよね。
ここから $\beta,z$ を求めます。
$\displaystyle\beta=2(2-i)\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)\\\displaystyle=2(2-i)\left(\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\\displaystyle=(2-i)(1+\sqrt{3}i)\\=2+2\sqrt{3}i-i+\sqrt{3}\\=2+\sqrt{3}+i(2\sqrt{3}-1)$
ここから $\beta$ をさらに $\displaystyle+\frac{\pi}{3}$ 回転して z を求めます。
$\displaystyle z=\{2+\sqrt3+i(2\sqrt{3}-1)\}\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)\\\displaystyle=\{(2+\sqrt{3})+i(2\sqrt{3}-1)\}\left(\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\\displaystyle=1+\frac{\sqrt{3}}{2}+\sqrt{3}i+\frac{3}{2}i+\sqrt{3}i-\frac{1}{2}i-3+\frac{\sqrt{3}}{2}\\\displaystyle=-2+\sqrt3+i(2\sqrt{3}+1)$
(答え)
SNSでシェア