【数II積分】曲線にかこまれた図形の面積を求める/解と係数の関係が成り立つ仕組み(北海道大2018)

$p$ を実数とする。関数 $y=x^3+px^2+x$ のグラフ $C_1$ と関数 $y=x^2$ のグラフ $C_2$ は，$x>0$ の範囲に共有点を2個もつとする。(北海道大2018)

(1) このような $p$ の値の範囲を求めよ。

(2) $C_1$ と $C_2$ の $x>0$ の範囲にある共有点の $x$ 座標をそれぞれ $\alpha$，$\beta(\alpha<\beta)$ とし，$0\leqq x\leqq\alpha$ と $\alpha\leqq x\leqq\beta$ の範囲で $C_1$ と $C_2$ が囲む部分の面積をそれぞれ $S_1$，$S_2$ とする。$S_1=S_2$ となるような $p$ の値を求めよ。また，このときの $S_1$ の値を求めよ。

２個の解がともに正であるときの条件

(1)から考えていきます。

共有点をもつことから，式を連立してみましょう。

$C_1:y=x^3+px^2+x$ ・・・①
$C_2:y=x^2$ ・・・②

として，①－②は

$x^3+(p-1)x^2+x=0$
$x\{x^2+(p-1)x+1\}=0$ ・・・③

ここで，③は $x=0$ のとき $=0$ となるので，$x=0$ は方程式の解です。しかし，問題文より $x>0$ だから，$x=0$ は不適です。

そこで，③を満たすもう一つの条件 $x^2+(p-1)x+1=0$ を考えてみましょう。

$f(x)=x^2+(p-1)x+1=0$ として

$x=0$ は不適だったので，$x>0$ で共有点を2個もつためには $f(x)=0$ が2個の実数解をもつ必要があります。

また，2個の解が $x>0$ を満たすためには，さらに条件が必要です。

・2個の実数解をもつことから，判別式 $D>0$。
・軸 > 0
・グラフが下に凸の場合は，$f(0)>0$

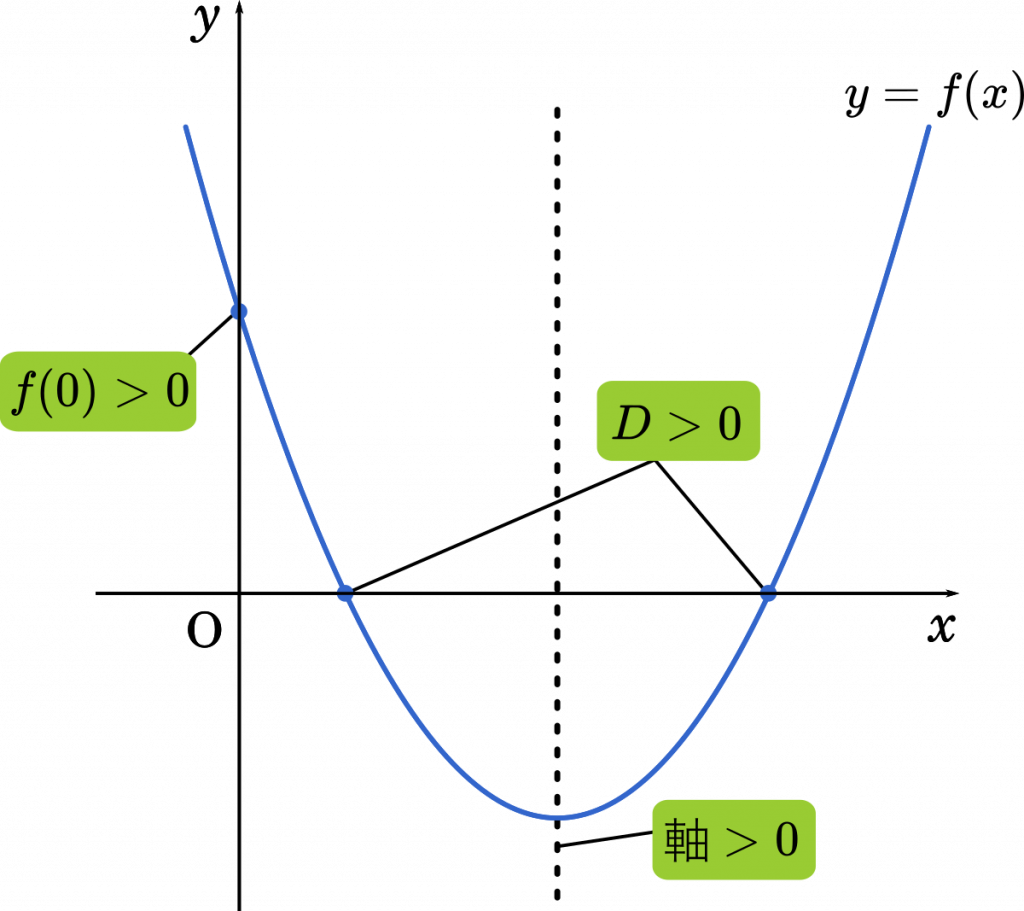
一つ目の条件から考えてきましょう。

$D=(p-1)^2-4>0$
$p^2-2p-3>0$
$(p-3)(p-1)>0$
$p<-1,3<p$ ・・・④

軸は公式として求めても良いですが，思い出せないときには平方完成しましょう。

$x^2+(p-1)x+1=0$
$\Big(x+\cfrac{p-1}{2}\Big)^2-\cfrac{(p-1)^2}{4}+1=0$

よって，軸は $-\cfrac{p-1}{2}$ ・・・⑤

軸>0 だから

$-\cfrac{p-1}{2}>0$
$-p+1>0$
$p<1$

また，$f(0)>0$ だから

$f(0)=1>0$ ・・・⑥

結果的に⑥は $p$ の値と関係ないので，不要であることが分かります。

あとは，④，⑤の条件，$p<-1,3<p$，$p<1$ を重ねます。

したがって

$p<-1$ (答え)

積分区間をつなげる

(2)に進みます。

今回はグラフが描けないとプラスマイナスの関係がおかしくなるので，グラフの概形を考えてみましょう。

まず，$C_1:y=x^3+px^2+x$ において，$x=0$ のとき $y=0$ となるので，グラフは原点を通ります。

また，式を微分すると

$y’=3x^2+2px+1$

となり，$x=0$ のとき $y’=1$ となります。つまり，グラフは原点において右上がりのグラフです。

また，$x>0$ で 共有点を2個もつことから，$C_1$ と $C_2$ は2箇所で交わります。

これらをもとに上のようなグラフが描ければよいでしょう。

また，原点以外で $C_1$ と $C_2$ が交わる点の $x$ 座標を $\alpha$，$\beta$ としておきます。

面積を求めるには積分を行います。考え方としてはグラフの上の曲線から下の曲線を引いた式を積分すれば良いです。

$\displaystyle S_1=\int_0^\alpha x^3+px^2+x-x^2\enspace dx$
$\displaystyle =\int_0^\alpha x^3+(p-1)x^2+x\enspace dx$
$\displaystyle S_2=\int_\alpha^\beta x^2-x^3-px^2-x\enspace dx$
$\displaystyle =-\int_\alpha^\beta x^3+(p-1)x^2+x\enspace dx$

$S_1=S_2$ より
$S_1-S_2=0$

$\displaystyle \int_0^\alpha x^3+(p-1)x^2+x\enspace dx+\int_\alpha^\beta x^3+(p-1)x^2+x\enspace dx=0$

式をよく見ると，2つの積分は同じ式で，積分区間が連続しています。このようなときは，積分区間をつなげて1つの式にしましょう。

$\displaystyle \int_0^\beta x^3+(p-1)x^2+x\enspace dx=0$
$\Big[\cfrac{1}{4}x^4+\cfrac{p-1}{3}x^3+\cfrac{x^2}{2}\Big]_0^\beta=0$
$\cfrac{1}{4}\beta^4+\cfrac{p-1}{3}\beta^3+\cfrac{1}{2}\beta^2=0$

問題文の条件より $\beta\not=0$ だから，両辺を $\beta^2$ でわると

$\cfrac{1}{4}\beta^2+\cfrac{p-1}{3}\beta+\cfrac{1}{2}=0$

両辺を12倍して

$3\beta^2+4(p-1)\beta+6=0$ ・・・⑦

この辺りで計算が手詰まりになるかもしれません。ましてや，$p$ の値が分かったとしても，$S_1$ を求めるには今度は $\alpha$ の値が必要です。

ここで，この問題のポイントになる部分ですが，$\alpha,\beta$ を求めるために解と係数の関係を利用しましょう。

解と係数の関係の簡単バージョン

解と係数の関係は公式を丸暗記するより，それが成り立つ仕組みを理解しましょう。

ここで，$x^2-3x+2=0$ という方程式を考えます。これは因数分解して
$(x-1)(x-2)=0$
となるので，解は $x=1,2$ です。

ここから，二次方程式の解が $\alpha,\beta$ のとき，次の関係が成り立つと言えます。

$(x-\alpha)(x-\beta)=0$

展開して

$x^2-(\alpha+\beta)x+\alpha\beta=0$

したがって，$x$ の項の係数が－解の和，定数の項が解の積を表していることが分かります。

最初の例で言えば，解が $1,2$ なら，$x$ の項の係数は $-(1+2)=-3$，定数の項は $1\times2=2$ となるので，関係が成り立っていることが確認できます。

教科書では，$x^2$ の項が $ax^2$ のような形になっている場合について公式が示されているのでもう少し複雑ですが，上の理解でも十分役立つので，まずは基本的な仕組みを理解しておきましょう。

解と係数の関係を利用して面積を求める

ここで，$\alpha,\beta$ は

$f(x)=x^2+(p-1)x+1=0$

の解であったことを思い出しましょう。よって

$\alpha+\beta=-(p-1)$
$\alpha\beta=1$

よって

$\alpha=\cfrac{1}{\beta}$

これを，$\alpha+\beta=-(p-1)$ に代入して

$\cfrac{1}{\beta}+\beta=-(p-1)$

両辺に $\beta$ をかけて

$1+\beta^2=-(p-1)\beta$
$\beta^2+(p-1)\beta+1=0$ ・・・⑧

ここで，先ほど作った式⑦と連立すれば，$p$ と $\beta$ を求めることができます。

⑦－⑧×3

$(p-1)\beta+3=0$
$\beta=-\cfrac{3}{p-1}$

⑧に代入して

$\Big(-\cfrac{3}{p-1}\Big)^2+(p-1)\Big(-\cfrac{3}{p-1}\Big)+1=0$
$\cfrac{9}{(p-1)^2}-3+1=0$
$\cfrac{9}{(p-1)^2}=2$
$2(p-1)^2=9$
$2p^2-4p+2=9$
$2p^2-4p-7=0$
$p=\cfrac{2\pm\sqrt{4+14}}{2}$
$p=\cfrac{2\pm3\sqrt{2}}{2}$

(1)より $p<-1$ だから

$p=\cfrac{2-3\sqrt{2}}{2}$

また，$\alpha=\cfrac{1}{\beta}$ と $\beta=-\cfrac{3}{p-1}$ から

$\alpha=-\cfrac{p-1}{3}$

が成り立ちます。

これを使って，$S_1$ を求めましょう。

$\displaystyle S_1=\int_0^\alpha x^3+(p-1)x^2+x\enspace dx$
$=\Big[\cfrac{x^4}{4}+\cfrac{p-1}{3}x^3+\cfrac{x^2}{2}\Big]_0^\alpha$
$=\cfrac{\alpha^4}{4}+\cfrac{p-1}{3}\alpha^3+\cfrac{\alpha^2}{2}$

$\alpha=-\cfrac{p-1}{3}$ より

$=\cfrac{\alpha^4}{4}-\alpha^4+\cfrac{\alpha^2}{2}$
$=-\cfrac{3}{4}\alpha^4+\cfrac{\alpha^2}{2}$

ここで，$\alpha$ の値を求めます。

$\alpha=-\cfrac{p-1}{3}$
$=-\cfrac{1}{3}\Big(\cfrac{2-3\sqrt{2}}{2}-1\Big)$
$=-\cfrac{1}{3}\Big(-\cfrac{3\sqrt{2}}{2}\Big)$
$=\cfrac{\sqrt{2}}{2}$

よって

$S_1=-\cfrac{3}{4}\Big(\cfrac{\sqrt{2}}{2}\Big)^4+\cfrac{1}{2}\Big(\cfrac{\sqrt{2}}{2}\Big)^2$
$=-\cfrac{3}{4}\cdot\cfrac{4}{16}+\cfrac{1}{2}\cdot\cfrac{2}{4}$
$=-\cfrac{3}{16}+\cfrac{1}{4}$
$=\cfrac{1}{16}$ (答え)