空間ベクトル・平面と直線の交点を求める（基本レベル）(神戸大2016文系第1問・理系第1問)

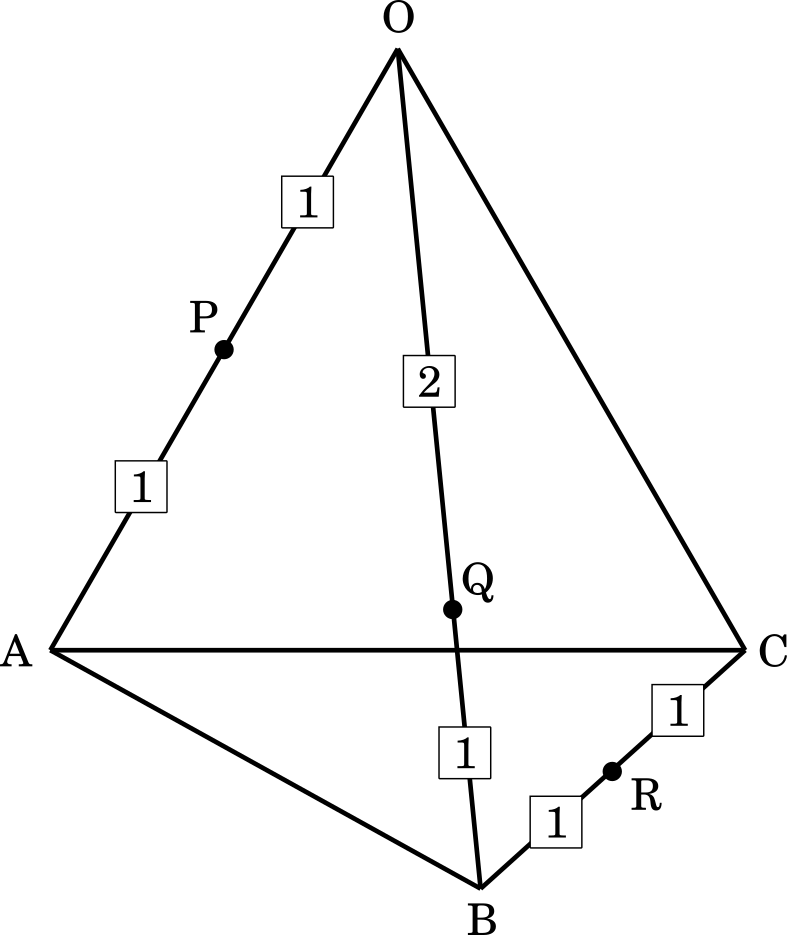
四面体 OABC において，P を辺 OA の中点，Q を辺 OB を 2 : 1 に内分する点，R を辺 BC の中点とする。P，Q，R を通る平面と辺 AC の交点を S とする。$\overrightarrow{\text{OA}}=\vec{a}$，$\overrightarrow{\text{OB}}=\vec{b}$，$\overrightarrow{\text{OC}}=\vec{c}$ とおく。以下の問に答えよ。

(1) $\overrightarrow{\text{PQ}}$，$\overrightarrow{\text{PR}}$ をそれぞれ $\vec{a},\vec{b},\vec{c}$ を用いて表わせ。

(2) 比 $|\overrightarrow{\text{AS}}|:|\overrightarrow{\text{SC}}|$ を求めよ。

(3) 四面体 OABC を 1 辺の長さが 1 の正四面体とするとき，$|\overrightarrow{\text{QS}}|$ を求めよ。

ベクトルの引き算

(1)から始めます。

$\overrightarrow{\text{PQ}}=\overrightarrow{\text{OQ}}-\overrightarrow{\text{OP}}$
$=\cfrac{2}{3}\vec{b}-\cfrac{1}{2}\vec{a}$
$=-\cfrac{1}{2}\vec{a}+\cfrac{2}{3}\vec{b}$　（答え）

また

$\overrightarrow{\text{PR}}=\overrightarrow{\text{OR}}-\overrightarrow{\text{OP}}$
$=\cfrac{1}{2}\vec{b}+\cfrac{1}{2}\vec{c}-\cfrac{1}{2}\vec{a}$
$=\cfrac{1}{2}(\vec{b}+\vec{c}-\vec{a})$　（答え）

平面と直線の交点

(2)に進みます。

点 S は PQR がつくる平面上にあるので

$\overrightarrow{\text{OS}}=s\overrightarrow{\text{OP}}+t\overrightarrow{\text{OQ}}+u\overrightarrow{\text{OR}}$　$(s+t+u=1)$　・・・①

と表すことができます。このとき，$s,t,u$ の値は何でも良いわけではなく，$s+t+u=1$ の関係が成り立つときにだけ平面上の点になります。

また，点 S は AC 上の点だから

$\overrightarrow{\text{AS}}=k\overrightarrow{\text{AC}}$ ・・・②

と表します。これによって

$|\overrightarrow{\text{AS}}|:|\overrightarrow{\text{SC}}|=k:1-k$

となるので，あとは連立方程式を解いて $k$ の値を求めましょう。

①より

$\overrightarrow{\text{OS}}=\cfrac{1}{2}s\vec{a}+\cfrac{2}{3}t\vec{b}+\cfrac{1}{2}u\vec{b}+\cfrac{1}{2}u\vec{c}$
$=\cfrac{1}{2}s\vec{a}+\Big(\cfrac{2}{3}t+\cfrac{1}{2}u\Big)\vec{b}+\cfrac{1}{2}u\vec{c}$　・・・③

よって

$\overrightarrow{\text{AS}}=\overrightarrow{\text{OS}}-\overrightarrow{\text{OA}}$
$=\Big(\cfrac{1}{2}s-1\Big)\vec{a}+\Big(\cfrac{2}{3}t+\cfrac{1}{2}u\Big)\vec{b}+\cfrac{1}{2}u\vec{c}$

これを②に代入すると

$\overrightarrow{\text{AS}}=k\overrightarrow{\text{AC}}$
$\Big(\cfrac{1}{2}s-1\Big)\vec{a}+\Big(\cfrac{2}{3}t+\cfrac{1}{2}u\Big)\vec{b}+\cfrac{1}{2}u\vec{c}=k\vec{c}-k\vec{a}$

ここで，左右の係数を比べましょう。

$\cfrac{1}{2}s-1=-k$　・・・④
$\cfrac{2}{3}t+\cfrac{1}{2}u=0$　・・・・⑤
$\cfrac{1}{2}u=k$　・・・⑥

あとは連立方程式を解いていけば良いことになります。ただし，ここでは $k$ の値さえ分かればよいということを念頭においた上で計算を進めていきます。

ここで $s+t+u=1$ の条件があったことを思い出しましょう。

④，⑤より

$\cfrac{1}{2}s-1=-\cfrac{1}{2}u$
$s-2=-u$
$s+u=2$

$s+t+u=1$ だから

$t+2=1$
$t=-1$

これを⑤に代入して

$-\cfrac{2}{3}+\cfrac{1}{2}u=0$
$\cfrac{1}{2}u=\cfrac{2}{3}$
$u=\cfrac{4}{3}$

これを⑥に代入して

$k=\cfrac{1}{2}\cdot\cfrac{4}{3}=\cfrac{2}{3}$

したがって

$|\overrightarrow{\text{AS}}|:|\overrightarrow{\text{SC}}|=k:1-k$
$=\cfrac{2}{3}:\cfrac{1}{3}=2:1$　（答え）

辺の長さを求める

(3)に進みます。

QS の長さを問われているので，とりあえず $\overrightarrow{\text{QS}}$ を求めてみましょう。

$\overrightarrow{\text{QS}}=\overrightarrow{\text{AS}}-\overrightarrow{\text{AQ}}$

$|\overrightarrow{\text{AS}}|:|\overrightarrow{\text{SC}}|=2:1$ より

$\overrightarrow{\text{AS}}=\cfrac{2}{3}\overrightarrow{\text{AC}}$

だから

$\overrightarrow{\text{QS}}=\cfrac{2}{3}\overrightarrow{\text{AC}}-\overrightarrow{\text{AQ}}$
$=\cfrac{2}{3}(\vec{c}-\vec{a})-(\overrightarrow{\text{OQ}}-\vec{a})$
$=\cfrac{2}{3}(\vec{c}-\vec{a})-\Big(\cfrac{2}{3}\vec{b}-\vec{a}\Big)$
$=\cfrac{1}{3}\vec{a}-\cfrac{2}{3}\vec{b}+\cfrac{2}{3}\vec{c}$
$=\cfrac{1}{3}(\vec{a}-2\vec{b}+2\vec{c})$

よって

$|\overrightarrow{\text{QS}}|^2=\cfrac{1}{9}(\vec{a}-2\vec{b}+2\vec{c})^2$

$=\cfrac{1}{9}(|\vec{a}|^2+4|\vec{b}|^2+4|\vec{c}|^2-4\vec{a}\cdot\vec{b}-8\vec{b}\cdot\vec{c}+4\vec{c}\cdot\vec{a})$

ここで，四面体の辺の長さがすべて 1 であることから，この四面体は正四面体であり，それぞれの面はすべて正三角形です。

OABC は正四面体だから

$\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}=1\cdot1\cdot\cos60\degree=\cfrac{1}{2}$

が成り立つ。よって

$|\overrightarrow{\text{QS}}|^2=\cfrac{1}{9}(1+4+4-2-4+2)$
$=\cfrac{5}{9}$

したがって

$|\overrightarrow{\text{QS}}|=\cfrac{\sqrt{5}}{3}$　（答え）