極値が 0 をとるとき，方程式が重解をとることを利用する(横浜国立大2020文系第3問)

実数 $a,b$ に対し，関数 $f(x)$ を

$f(x)=-x^3+(a+2)x^2-(3a-b-2)x-3(b-1)$
と定める。$xy$ 平面上で $y=f(x)$ の表す曲線を $C$ とする。次の問いに答えよ。

(1) どのような $a,b$ の値に対しても，$C$ はある定点を通ることを示せ。

(2) $f(x)$ は極値をとるとする。$C$ が $x$ 軸に接するような $(a,b)$ の存在範囲を $ab$ 平面上に図示せよ。

(3) $(a,b)$ が(2)で求めた範囲にあるとき，$f(x)$ の極値を $a$ の式で表せ。

a, b が 0 になる条件を考える

(1)から始めます。

$y=f(x)$ として，$x$ に何らかの値を代入すると $y$ は $a,b$ を含む値になります。これでは $a,b$ の値によって $y$ もさまざまな値をとることになります。

そこから，定点を通るということは，$y$ が $a,b$ を含まない数になれば良い，ということが分かります。

いったん，式の $a,b$ をそれぞれまとめてみましょう。

$f(x)=-x^3+(a+2)x^2-(3a-b-2)x-3(b-1)$
$=-x^3+ax^2+2x^2-3ax+bx+2x-3b+3$
$=-x^3+2x^2+2x+3+a(x^2-3x)+b(x-3)$

$x^2-3x=0$ かつ $x-3=0$ であれば，式から $a,b$ が消えます。

$x^3-3x=0$
$x(x-3)=0$

$x=0,3$

また

$x-3=0$
$x=3$

よって，$x=3$

$f(3)=-27+18+6+3=0$

したがって，$f(x)$ は定点 $(3,0)$ を通る。（答え）

極値が 0 をとるとき，方程式が重解をとることを利用する

(2)に進みます。

$f(x)=-x^3+(a+2)x^2-(3a-b-2)x-3(b-1)$ より
$f'(x)=-3x^2+2(a+2)x-3a+b+2$

$C$ が $x$ に接するということは，極値のうちの一つが $x$ 軸に接するということと同じことです。

$C$ は必ず $(3,0)$ を通るので，まずは $x=3$ で極値をとる場合を考えてみましょう。

(i) $x=3$ で極値をとるとき

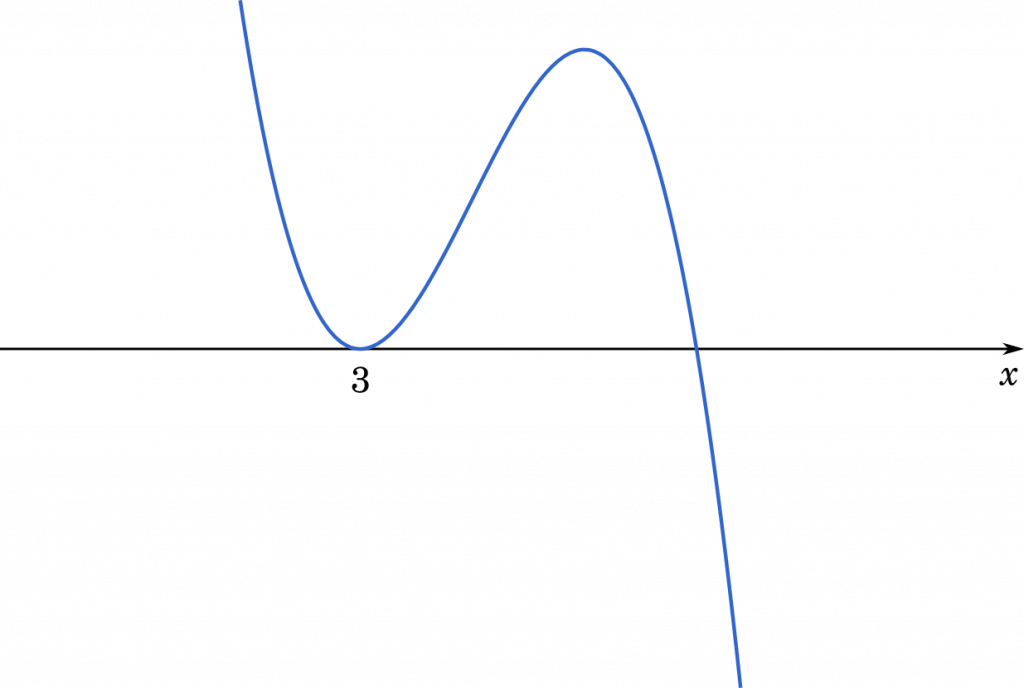
$f'(3)=-27+6a+12-3a+b+2=0$
$3a+b-13=0$
$b=-3a+13$　・・・①

横軸を $a$，縦軸を $b$ とするグラフを描くとすると，これは直線になります。

(ii) $x=3$ 以外で極値をとるとき

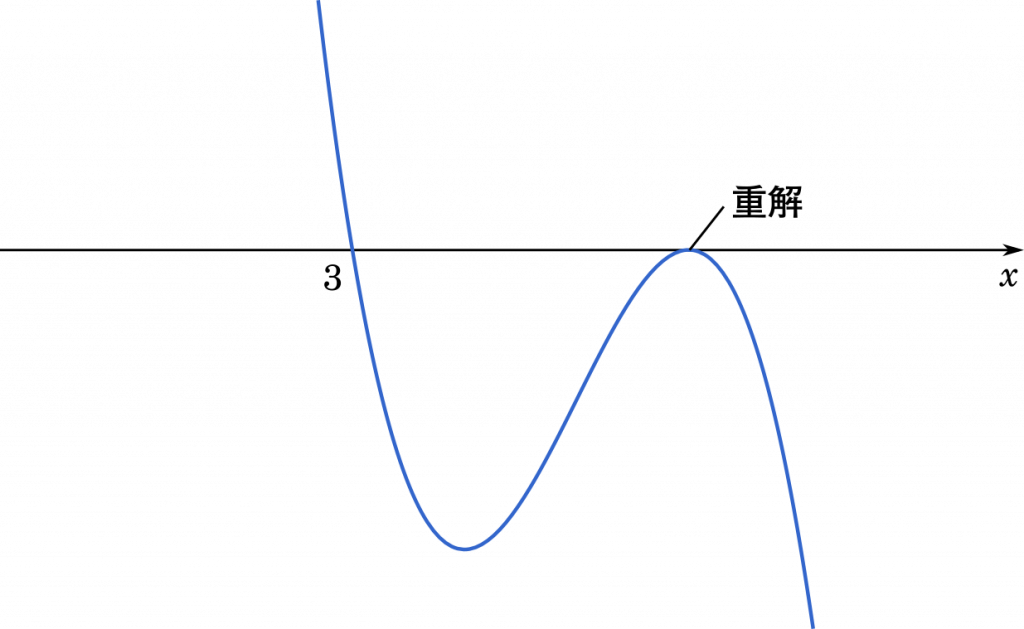
グラフを描いてみると分かりますが，$f(x)$ は $x$ 軸と 2 点で交わります。そして，このとき，$f(x)$ の $x=3$ 以外の解は重解をとります。

ここで，$f(x)$ が $x=3$ を解にもつことが分かっているので，いったん因数分解してみましょう。

組立除法を用いて

$f(x)=-x^3+(a+2)x^2-(3a-b-2)x-3(b-1)$

$\begin{matrix}-1&a+2&-3a+b+2&-3b+3&|\underline{3}\\&-3&3a-3&3b-3\\\hline-1&a-1&b-1&0 \end{matrix}$

$(x-3)\{-x^2+(a-1)x+b-1\}=0$

ここで，$\{-x^2+(a-1)x+b-1\}=0$ が重解ともつとすると，判別式 $D=0$ より

$D=(a-1)-2+4(b-1)=0$
$a^2-2a+1-2+4b-4=0$
$a^2-2a+4b-3=0$ ・・・②
$4b=-a^2+2a+3$
$b=-\cfrac{1}{4}(a^2-2a-3)$
$=-\cfrac{1}{4}(a-3)(a+1)$

このグラフは上に凸の曲線で，$x$ 軸と $-1,3$ で交わります。また，平方完成して頂点も求めておきましょう。

$b=-\cfrac{1}{4}(a^2-2a-3)$ より
$=-\cfrac{1}{4}(a^2-2a)+\cfrac{3}{4}$
$=-\cfrac{1}{4}(a-1)^2+\cfrac{1}{4}+\cfrac{3}{4}$
$=-\cfrac{1}{4}(a-1)^2+1$

頂点の座標は $(1,1)$

これで，描くグラフは傾きがマイナスの直線と，上に凸の二次関数のグラフであることが分かりました。ただし，この２つのグラフはどこかで交点を持つかもしれません。そのときには，グラフに交点の座標も書き込む必要があります。

①を②に代入すると

$a^2-2a+4(-3a+13)-3=0$
$a^2-2a-12a+52-3=0$
$a^2-14a+49=0$
$(a-7)^2=0$
$a=7$

①に代入して

$b=-3\cdot7+13$
$=-8$

よって①と②は $(7,-8)$ で接する。

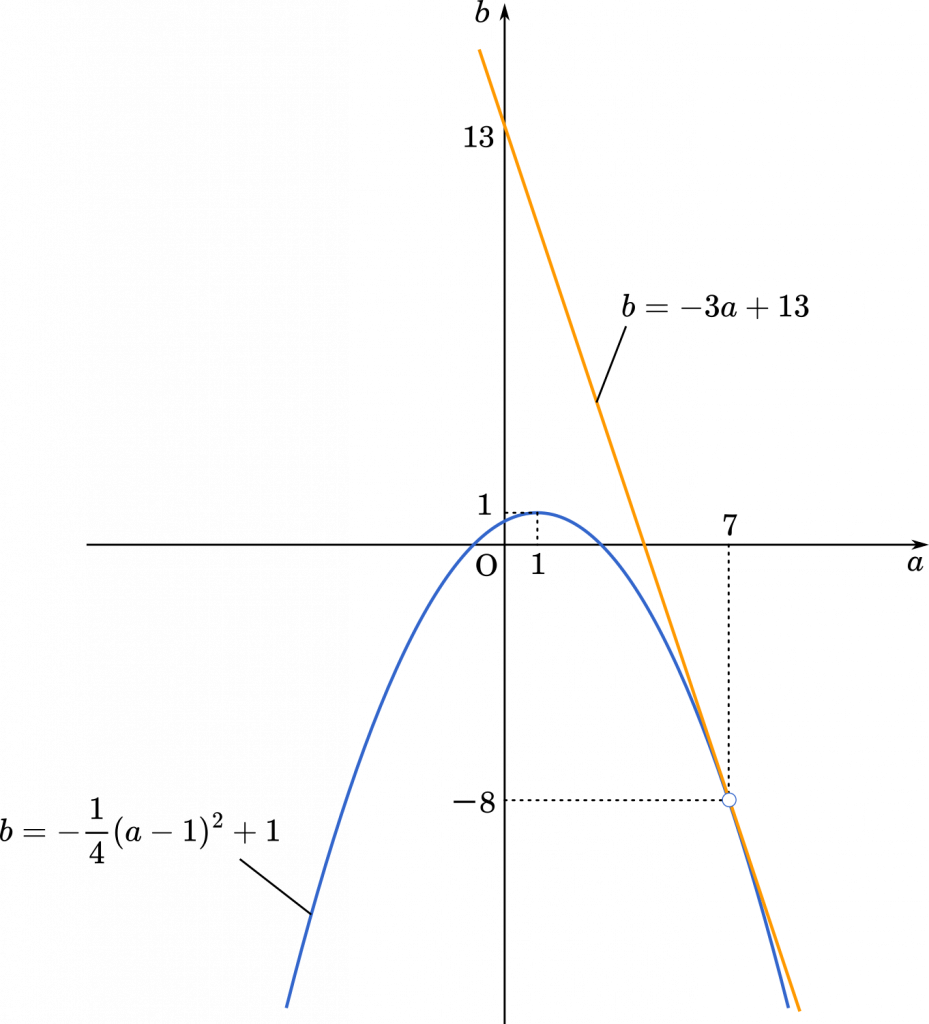
（答え）

極値を求める

(3)に進みます。

三次関数は，重解をもたずに，異なる 3 つの実数解をもつ場合，極値が 2 か所できます。そのうちの一つが極小値で，もう一つが極大値です。よって，ここでは極小値と極大値を求めていきます。

(i) $x=3$ で極値をとるとき

このとき，$(3,0)$ は極小値か極大値のどちらかです。もう一つの極値を求めて，比べてみましょう。

$x=3$ で極値をとるとき $b=-3a+13$ が成り立つので，これを代入して

$f'(x)=-3x^2+2(a+2)x-3a-3a+13+2$
$=-3x^2+2(a+2)x-6a+15$

ここから，もう一つの解を求めます。方法はいくつかありますが，解と係数の関係を用いるのが手っ取り早いです。

$-3x^2+2(a+2)x-6a+15=0$ の解を $3,\beta$ とすると
$3+\beta=\cfrac{2a+4}{3}$
$\beta=\cfrac{2a-5}{3}$

極値を求めると

$f(x)=(x-3)\{-x^2+(a-1)x+b-1\}$

$b=-3a+13$ を代入して

$=(x-3)\{-x^2+(a-1)x+3a+13-1\}$
$=(x-3)\{-x^2+(a-1)x+3a+12\}$

$x=3$ で極値をとるとき，$x=3$ で重解をとります。よって，$-x^2+(a-1)x+3a+12$ は $x-3$ で割り切れるはずです。

$\begin{matrix}-1&a-1&3a+12&|\underline{3}\\&-3&3a-12\\\hline-1&a-4&0\end{matrix}$

$=(x-3)^2(-x+a-4)$

よって

$f\Big(\cfrac{2a-5}{3}\Big)=\Big(\cfrac{2a-5}{3}-3\Big)^2\Big(-\cfrac{2a-5}{3}+a-4\Big)$
$=\Big(\cfrac{2a-14}{3}\Big)^2\cdot\cfrac{a-7}{3}$
$=\cfrac{4}{27}(a-7)^3$

$a$ が 7 より大きいとき $f(x)$ は 0 より大きく，7 より小さいときは $f(x)$ は 0 より小さくなります。

したがって

$a>7$ かつ $b=-3a+13$ のとき，$x=3$ で極小値 $0$，極大値 $\cfrac{4}{27}(a-7)^3$ をとり，$a<7$ かつ $b=-3a+13$ のとき，$x=3$ で極小値 $\cfrac{4}{27}(a-7)^3$，極大値 $0$ をとる。（答え）

ここで，$a=7$ とすると，$f(x)=0$ となります。しかし，3 次関数のグラフを描いてみると分かりますが，極大値と極小値がともに 0 になるというグラフは描けないはずです。この時点で $a=7$ のとき，$f(x)=0$ が三重解をとることに気づけば，(1)の答えを修正できるでしょう。

(ii) $x=3$ 以外で極値をとるとき

$b=-\cfrac{1}{4}(a-1)^2+1$ が成り立つので，これを代入して

$f(x)=(x-3)\{-x^2+(a-1)x+b-1\}$
$=(x-3)\Big\{-x^2+(a-1)x-\cfrac{1}{4}(a-1)^2\Big\}$
$=-(x-3)\Big\{x^2-(a-1)x+\cfrac{1}{4}(a-1)^2\Big\}$
$=-(x-3)\Big(x-\cfrac{a-1}{2}\Big)^2$

よって，$x=3$ 以外に $x=\cfrac{a-1}{2}$ で $x$ 軸に接し，このとき極値をとります。

極値はあともう一つ存在するので，求めていきましょう。

$f'(x)$ に $b=-\cfrac{1}{4}(a-1)^2+1$ を代入して

$f'(x)=-3x^2+2(a+2)x-3a-\cfrac{1}{4}(a-1)^2+3$

$-3x^2+2(a+2)x-3a-\cfrac{1}{4}(a-1)^2+3=0$ とすると
解の一つは $\cfrac{a-1}{2}$ です。もう一つの解を，解と係数の関係を利用して求めます。

$\cfrac{a-1}{2}+\beta=\cfrac{2}{3}(a+2)$
$\beta=\cfrac{2}{3}a+\cfrac{4}{3}-\cfrac{a}{2}+\cfrac{1}{2}$
$=\cfrac{a+11}{6}$

$f(x)$ に代入して

$f\Big(\cfrac{a+11}{6}\Big)=-\Big(\cfrac{a+11}{6}-3\Big)\Big(\cfrac{a+11}{6}-\cfrac{a-1}{2}\Big)^2$
$=-\cfrac{1}{6^3}(a+11-18)(a+11-3a+3)^2$
$=-\cfrac{1}{6^3}(a-7)(-2a+14)^2$
$=-\cfrac{4}{6^3}(a-7)^3$
$=-\cfrac{1}{54}(a-7)^3$

$a>7$ かつ $b=-\cfrac{1}{4}(a-1)^2+1$ のとき，$x=\cfrac{a+11}{6}$ で極小値 $-\cfrac{1}{54}(a-7)^3$，$x=\cfrac{a-1}{2}$ で 極大値 $0$ をとり，$a<7$ かつ $b=-\cfrac{1}{4}(a-1)^2+1$ のとき，$x=\cfrac{a-1}{2}$ で極小値 $0$，$x=\cfrac{a+11}{6}$ で極大値 $0$ をとる。（答え）