【スマホで読む・わかりやすい】共通テスト数学IA2021本試【解説・正解・問題】
第2問 正解
ア 2 イウ -2 エオ 44 カ.キク 2.00
ケ.コサ 2.20 シ.スセ 4.40
ソ 3 タ,チ 1,3 (解答の順序は問わない)
ツ 1 テ 4 ト 5 ナ 2
〔1〕(1)
ピッチ $z$ は 1 秒あたりの歩数,ストライド $x$ は 1 歩あたりの進む距離だから
$x$ × 全体の歩数 = 100(m)
$z$ × タイム = 全体の歩数
が成り立つ。これより
全体の歩数 = $\cfrac{100}{x}$
タイム = $\cfrac{\sf 全体の歩数}{z}$
値を代入すると
タイム = $\cfrac{\enspace\cfrac{100}{x}\enspace}{z}=\cfrac{\enspace\cfrac{100}{x}\times x\enspace}{z\times x}$
$=\cfrac{100}{xz}$
・・・・・・ア
〔1〕(2)
$z=ax+b$ として
直線の傾き $a$ は $\cfrac{z\sf の増加量}{x\sf の増加量}$ だから
$\cfrac{-0.1}{0.05}=-2$
データより,$x=2.05$,$z=4.70$ を代入すると
$4.70=-2\times2.05+b$
$4.70=-4.1+b$
$b=8.8=\cfrac{44}{5}$
したがって
$z=-2x+\cfrac{44}{5}$ ・・・・・・②
・・・・・・イウエオ
次に $x$ の範囲を考える。②は右下がりのグラフだから,ピッチの最大値 $4.80$ のときに $x$ は最小値をとる。

$4.80=-2x+\cfrac{44}{5}$
上で,$8.8=\cfrac{44}{5}$ だったので
$2x=8.8-4.80=4$
$x=2.00$
したがって
$2.00\leqq x\leqq2.40$
・・・・・・カキク
さらに $y=xz$ とおく。
②を代入して
$y=x\Big(-2x+\cfrac{44}{5}\Big)$
$=-2x^2+\cfrac{44}{5}x$
$y$ の最大値を求めるために,平方完成すると
$y=-2\Big(x^2-\cfrac{22}{5}x\Big)$
$=-2\Big(x-\cfrac{11}{5}\Big)^2-\cfrac{(-2)\times11^2}{5}$
$=-2\Big(x-\cfrac{11}{5}\Big)^2+\cfrac{242}{25}$
グラフは上に凸であるから,$x=\cfrac{11}{5}$ のときに $y$ は最大となる。
したがって
$x=\cfrac{11}{5}=2.20$
・・・・・・ケコサ
このときのピッチ $z$ を求めると,$x=2.20$ を②に代入して
$z=-2\times2.20+\cfrac{44}{5}$
$=-4.40+8.8=4.40$
・・・シスセ
タイムを求めると,①より
タイム=$\cfrac{100}{xz}$
$=\cfrac{100}{2.20\times.4.40}$
$=\cfrac{100}{9.68}=10.33\cdots$
したがって,選択肢の中で最も適当なものは③ $10.33$ である。
・・・・・・ソ
〔2〕(1)

⓪ 正しい。
① 1990年度は右側の方が長い。よって正しくない。
② 正しい。
③ 1975年度と1980年度を比べると,増加している。よって正しくない。
④ 正しい。
⑤ 正しい。
したがって,正しくないものは①と③。
・・・・・タチ
〔2〕(2)
・1985年度におけるグラフ
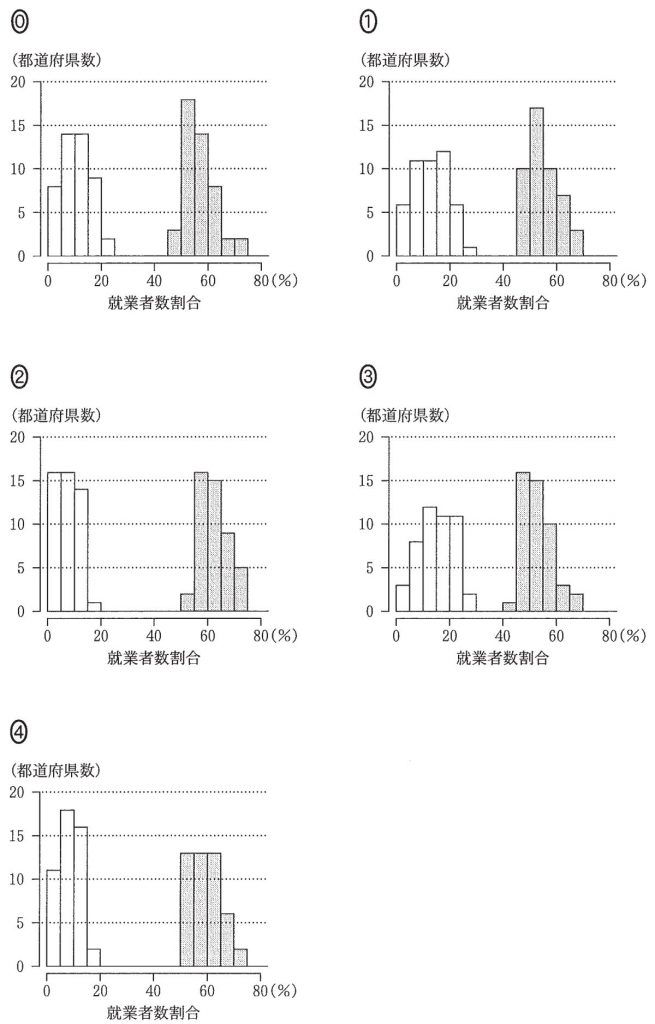
図1より,第3次産業の就業者数割合の最小値は 45% であるため,選択肢は⓪か①に絞られる。
また,図1より,最大値は 65% 以上 75% 未満であり,⓪には 70% 以上のデータがあるので,不適。
したがって,①が最も適当である。
・・・・・・ツ
・1995年度におけるグラフ
図1より,第3次産業の就業者数割合の最小値は 50% 以上 55% 未満であるため,選択肢は②か④に絞られる。ここで,$Q_1$ を考えると
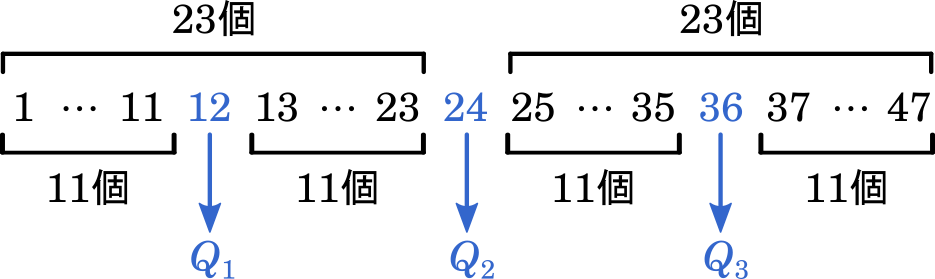
$Q_1$ は小さい方から数えて 12 番目である。
図1より,第1次産業の就業者数割合の$Q_1$ は 10% 以上 15% 未満である。②は 0 以上 5% 未満に小さい方から数えて 12 番目のデータが含まれるため,不適。
したがって,④が最も適当である。
・・・・・・テ
〔2〕(3)
(I) 相関は弱くなっている。誤。
(II) 正しい。
(III) 相関は弱くなっている。誤
したがって,⑤が正しい。
・・・・・・ト
〔2〕(4)
男性と女性の割合を考えると,例えば,男性の割合が 45% であれば,女性の割合は 55% である。また,男性の割合が 40 % であれば,女性の割合は 60% である。
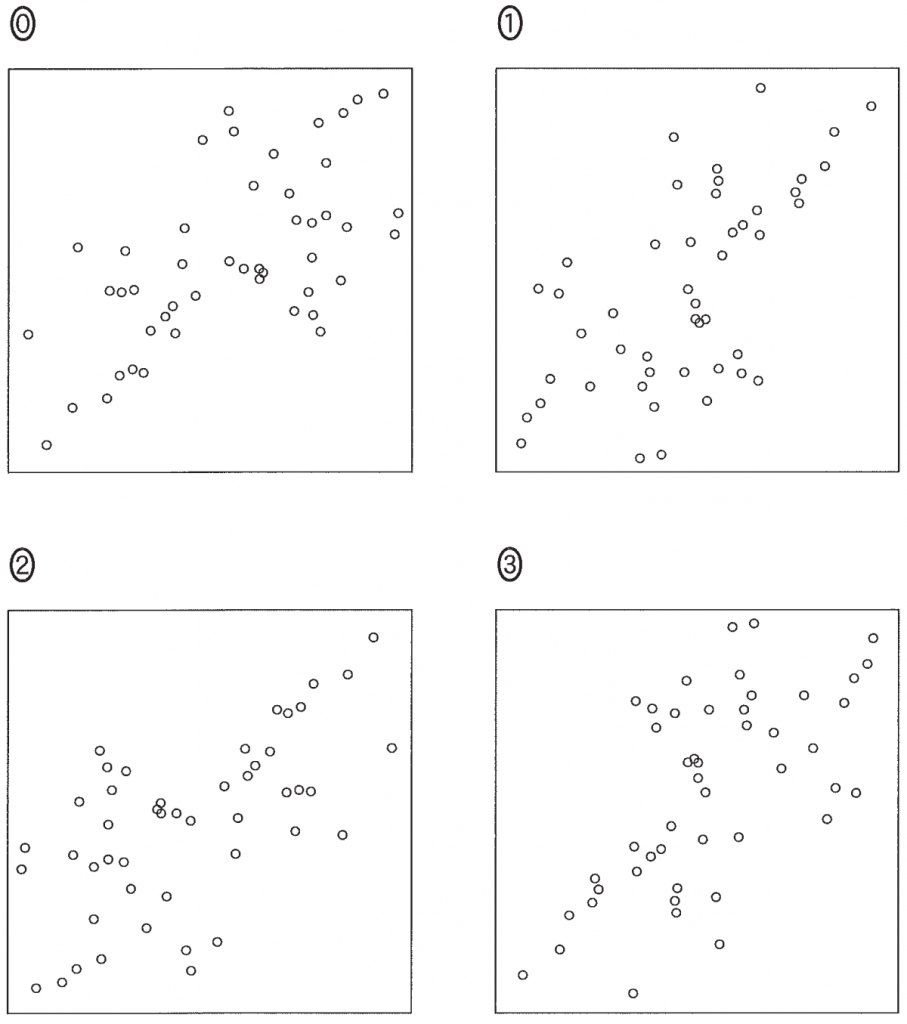
このように考えると,女性の就業者数割合の散布図は図4を上下反転したものであると言える。
したがって,②が最も適当である。
・・・・・・ナ
問題文
第2問
〔1〕 陸上競技の短距離 100m 走では,100 m を走るのにかかる時間(以下,タイムと呼ぶ)は,1 歩あたりの進む距離(以下,ストライドと呼ぶ)と 1 秒あたりの歩数(以下,ピッチと呼ぶ)に関係がある。
ストライドとピッチはそれぞれ以下の式で与えられる。
ストライド(m/歩) = $\cfrac{\text{100(m)}}{\text{100 m を走るのにかかった歩数(歩)}}$
ピッチ(歩/秒) = $\cfrac{\text{100 m を走るのにかかった歩数(歩)}}{\text{タイム(秒)}}$
ただし,100 m を走るのにかかった歩数は,最後の 1 歩がゴールラインをまたぐこともあるので,小数で表される。以下,単位は必要のない限り省略する。
例えば,タイムが $10.81$ で,そのときの歩数が $48.5$ であったとき,ストライドは $\cfrac{100}{48.5}$ より約 $2.06$,ピッチは $\cfrac{48.5}{10.81}$ より約 $4.49$ である。
なお,小数の形で解答する場合は,解答上の注意にあるように,指定された桁数の一つ下の桁を四捨五入して答えよ。また,必要に応じて,指定された桁まで⓪にマークせよ。
(1) ストライドを $x$,ピッチを $z$ とおく。ピッチは 1 秒あたりの歩数,ストライドは 1 歩あたりの進む距離なので,1 秒あたりの進む距離すなわち平均速度は,$x$ と $z$ を用いて $\boxed{\boxed{\sf ア}}$ (m/秒)と表される。
これより,タイムと,ストライド,ピッチとの関係は
タイム = $\cfrac{100}{\boxed{\boxed{\text{ア}}}}$ ・・・・・・①
と表されるので, ${\boxed{\boxed{\text{ア}}}}$ が最大になるときにタイムが最もよくなる。ただし,タイムがよくなるとは,タイムの値が小さくなることである。
${\boxed{\boxed{\text{ア}}}}$ の解答群
⓪ $x+z$ ① $z-x$ ② $xz$
③ $\cfrac{x+z}{2}$ ⑤ $\cfrac{z-x}{2}$ ⑥ $\cfrac{xz}{2}$
(2) 男子短距離 100 m 走の選手である太郎さんは,① に着目して,タイムが最もよくなるストライドとピッチを考えることにした。
次の表は,太郎さんが練習で 100 m を 3 回走ったときのストライドとピッチのデータである。
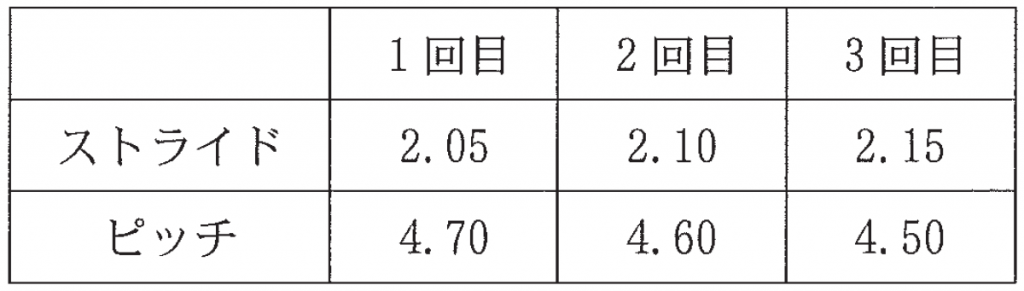
また,ストライドとピッチにはそれぞれ限界がある。太郎さんの場合,ストライドの最大値は $2.40$,ピッチの最大値は $4.80$ である。
太郎さんは,上の表から,ストライドが $0.05$ 大きくなるとピッチが $0.1$ 小さくなるという関係があると考えて,ピッチがストライドの 1 次関数として表されると仮定した。このとき,ピッチはストライドを用いて
$z=\boxed{\sf イウ}+\cfrac{\boxed{\sf エオ}}{5}$ ・・・・・・②
と表される。
②が太郎さんのストライドの最大値 $2.40$ とピッチの最大値 $4.80$ まで成り立つと仮定すると,$x$ の値の範囲は次のようになる。
$\boxed{\sf カ}.\enspace\boxed{\sf キク}\leqq x\leqq2.40$
$y=\boxed{\sf ア}$ とおく。② を $y=\boxed{\sf ア}$ に代入することにより,$y$ を $x$ の関数として表すことができる。太郎さんのタイムが最もよくなるストライドとピッチを求めるためには,$\boxed{\text{カ}}.\enspace\boxed{\text{キク}}\leqq x \leqq2.40$ の範囲で $y$ の値を最大にする $x$ の値を見つければよい。このとき,$y$ の値が最大になるのは $x=\boxed{\sf ケ}.\enspace\boxed{\sf コサ}$ のときである。
よって,太郎さんのタイムが最もよくなるのは,ストライドが $x=\boxed{\text{ケ}}.\enspace\boxed{\text{コサ}}$ のときであり,このとき,ピッチは,$x=\boxed{\sf シ}.\enspace\boxed{\sf スセ}$ である。また,このときの太郎さんのタイムは,① により,$\boxed{\boxed{\sf ソ}}$ である。
$\boxed{\boxed{\text{ソ}}}$ については,最も適当なものを次の⓪~⑤のうちから一つ選べ。
⓪ $9.68$ ① $9.97$
② $10.09$ ④ $10.33$
⑤ $10.42$ ⑤ $10.55$
〔2〕 就業者の従事する産業は,勤務する事業所の主な経済活動の種類によって,第 1 次産業(農業,林業と漁業),第 2 次産業(鉱業,建設業と製造業),第 3 次産業(前記以外の産業)の三つに分類される。国の労働状況の調査(国勢調査)では,47 の都道府県別に第 1 次,第 2 次,第 3 次それぞれの産業ごとの就業者数が発表されている。ここでは都道府県別に,就業者数に対する各産業に就業する人数の割合を算出したものを,各産業の「就業者数割合」と呼ぶことにする。
(1) 図 1 は,1975 年度から 2010 年度まで 5 年ごとの 8 個の年度(それぞれを時点という)における都道府県別の三つの産業の就業者数割合を箱ひげ図で表したものである。各時点の箱ひげ図は,それぞれ上から順に第 1 次産業,第 2 次産業,第 3 次産業のものである。

図 1 三つの産業の就業者数割合の箱ひげ図
(出典:総務省の Web ページにより作成)
次の⓪~⑤のうち,図 1 から読み取れることとして正しくないものは $\boxed{\boxed{\sf タ}}$ と $\boxed{\boxed{\sf チ}}$ である。
$\boxed{\boxed{\text{タ}}}$,$\boxed{\boxed{\text{チ}}}$ の解答群(解答の順序は問わない。)
⓪ 第 1 次産業の就業者数割合の四分位範囲は,2000 年度までは,後の時点になるにしたがって減少している。
① 第 1 次産業の就業者数割合について,左側のひげの長さと右側のひげの長さを比較すると,どの時点においても左側の方が長い。
② 第 2 次産業の就業者数割合の中央値は,1990 年度以降,後の時点になるにしたがって減少している。
③ 第 2 次産業の就業者数割合の第 1 四分位数は,後の時点になるにしたがって減少している。
④ 第 3 次産業の就業者数割合の第 3 四分位数は,後の時点になるにしたがって増加している。
⑤ 第 3 次産業の就業者数割合の最小値は,後の時点になるにしたがって増加している。
(2) (1)で取り上げた 8 時点の中から 5 時点を取り出して考える。各時点における都道府県別の,第 1 次産業と第 3 次産業の就業者数割合のヒストグラムを一つのグラフにまとめてかいたものが,次ページの五つのグラフである。それぞれの右側の網掛けしたヒストグラムが第 3 次産業のものである。なお,ヒストグラムの各階級の区間は,左側の数値を含み,右側の数 値を含まない。
・1985 年度におけるグラフは $\boxed{\boxed{\sf ツ}}$ である。
・1995 年度におけるグラフは $\boxed{\boxed{\sf テ}}$ である。
$\boxed{\boxed{\text{ツ}}}$,$\boxed{\boxed{\text{テ}}}$ については,最も適当なものを,次の⓪~④のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
(3) 三つの産業から二つずつを組み合わせて都道府県別の就業者数割合の散布図を作成した。図 2 の散布図群は,左から順に 1975 年度における第 1 次産業(横軸) と第 2 次産業(縦軸)の散布図,第 2 次産業(横軸) と第 3 次産業(縦軸) の散布図,および第 3 次産業(横軸)と第 1 次産業(縦軸)の散布図である。また,図 3 は同様に作成した 2015 年度の散布図群である。
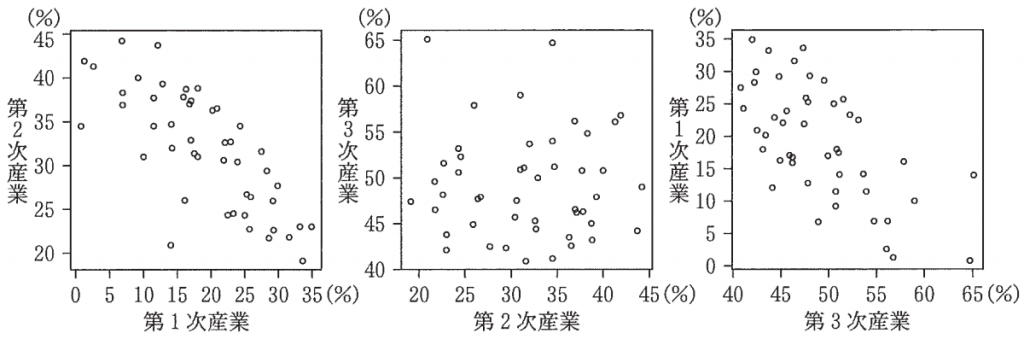
図2 1975 年度の散布図群
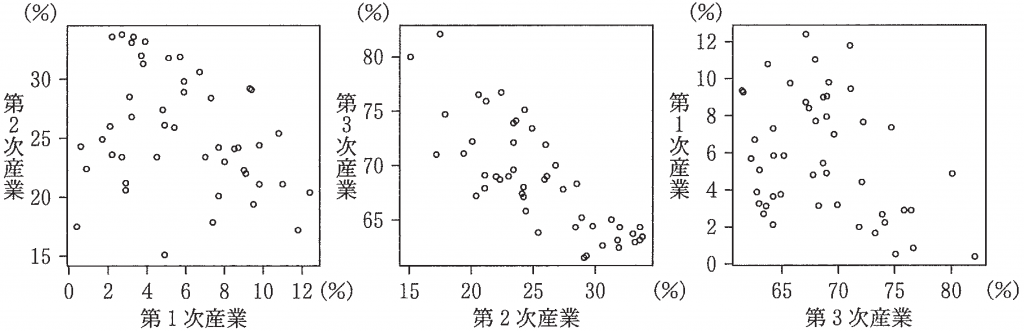
図3 2015 年度の散布図群
(出典:図 2,図 3 はともに総務省の Web ページにより作成)
下の (I),(II),(III) は,1975 年度を基準としたときの,2015 年度の変化を記述したものである。ただし,ここで「相関が強くなった」とは,相関係数の絶対値が大きくなったことを意味する。
(I) 都道府県別の第 1 次産業の就業者数割合と第 2 次産業の就業者数割合の間の相関は強くなった。
(II) 都道府県別の第 2 次産業の就業者数割合と第 3 次産業の就業者数割合の間の相関は強くなった。
(III) 都道府県別の第 3 次産業の就業者数割合と第 1 次産業の就業者数割合の間の相関は強くなった。
(I),(II),(III) の正誤の組合せとして正しいものは,$\boxed{\boxed{\sf ト}}$ である。
$\boxed{\boxed{\text{ト}}}$ の解答群
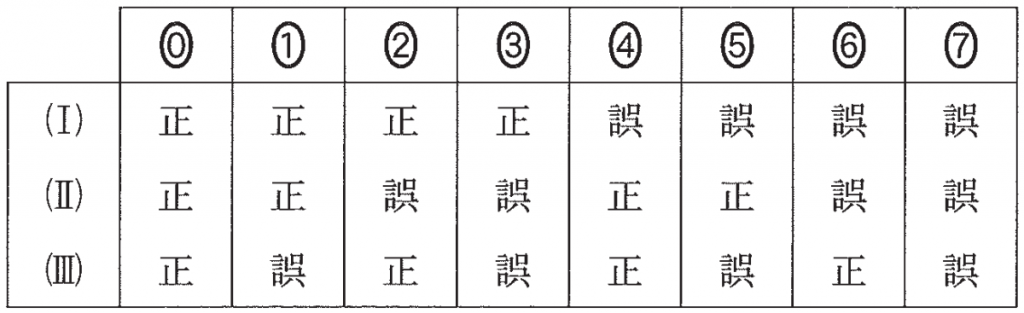
(4) 各都道府県の就業者数の内訳として男女別の就業者数も発表されている。そこで,就業者数に対する男性・女性の就業者数の割合をそれぞれ「男性の就業者数割合」,「女性の就業者数割合」と呼ぶことにし,これらを都道府県別に算出した。図 4 は,2015 年度における都道府県別の,第 1 次産業の就業者数割合(横軸) と,男性の就業者数割合(縦軸) の散布図である。
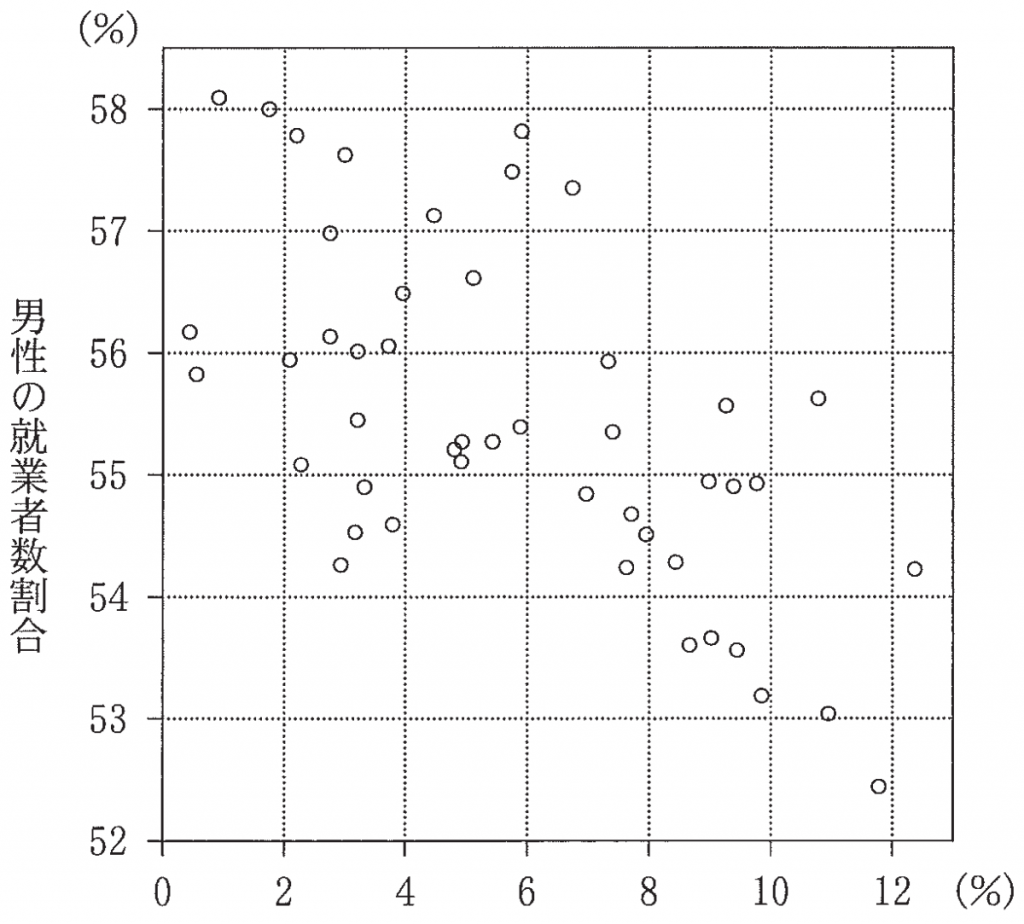
図4 都道府県別の,第1次産業の就業者数割合と,男性の就業者数割合の散布図
(出典:総務省の Web ページにより作成)
各都道府県の,男性の就業者数と女性の就業者数を合計すると就業者数の全体となることに注意すると,2015 年度における都道府県別の,第1次産業の就業者数割合(横軸) と,女性の就業者数割合(縦軸) の散布図は $\boxed{\boxed{\sf ナ}}$ である。
$\boxed{\boxed{\text{ナ}}}$ については,最も適当なものを,下の⓪~③のうちから一つ選 べ。なお,設問の都合で各散布図の横軸と縦軸の目盛りは省略しているが,横軸は右方向,縦軸は上方向がそれぞれ正の方向である。
SNSでシェア