【複素数平面】共役な複素数がつくる三角形の面積(神戸大2018理系第４問)

整式 $f(x)$ は実数を係数にもつ 3 次式で，3 次の係数は 1，定数項は $-3$ とする。方程式 $f(x)=0$ は，1 と虚数 $\alpha,\beta$ を解にもつとし，$\alpha$ の実部は 1 より大きく，$\alpha$ の虚部は正とする。複素数平面上で $\alpha,\beta,1$ が表す点を順に A，B，C とし，原点を O とする。以下の問に答えよ。

(1) $\alpha$ の絶対値を求めよ。

(2) $\theta$ を $\alpha$ の偏角とする。△ABC の面積 $S$ を $\theta$ を用いて表わせ。

(3) $S$ を最大にする $\theta$ $(0\leqq\theta\leqq2\pi)$ とそのときの整式 $f(x)$ を求めよ。

3 次方程式の解

(1)から始めます。

$1,\alpha,\beta$ を解にもつ 3 次方程式は次のように表せます。

$f(x)=(x-1)(x-\alpha)(x-\beta)$

展開すると

$=\{x^2-(1+\alpha)x+\alpha\}(x-\beta)$
$=x^3-(1+\alpha+\beta)x^2+(\beta+\alpha\beta+\alpha)x-\alpha\beta$

定数項は $-3$ だから

$\alpha\beta=3$

また，$\alpha$ と $\beta$ はたがいに共役な複素数だから

$\beta=\overline{\alpha}$

と表せます。よって

$|\alpha|^2=\alpha\overline{\alpha}$
$=\alpha\beta=3$

したがって

$|\alpha|=\sqrt{3}$　（答え）

三角形の面積を求める

(2)に進みます。

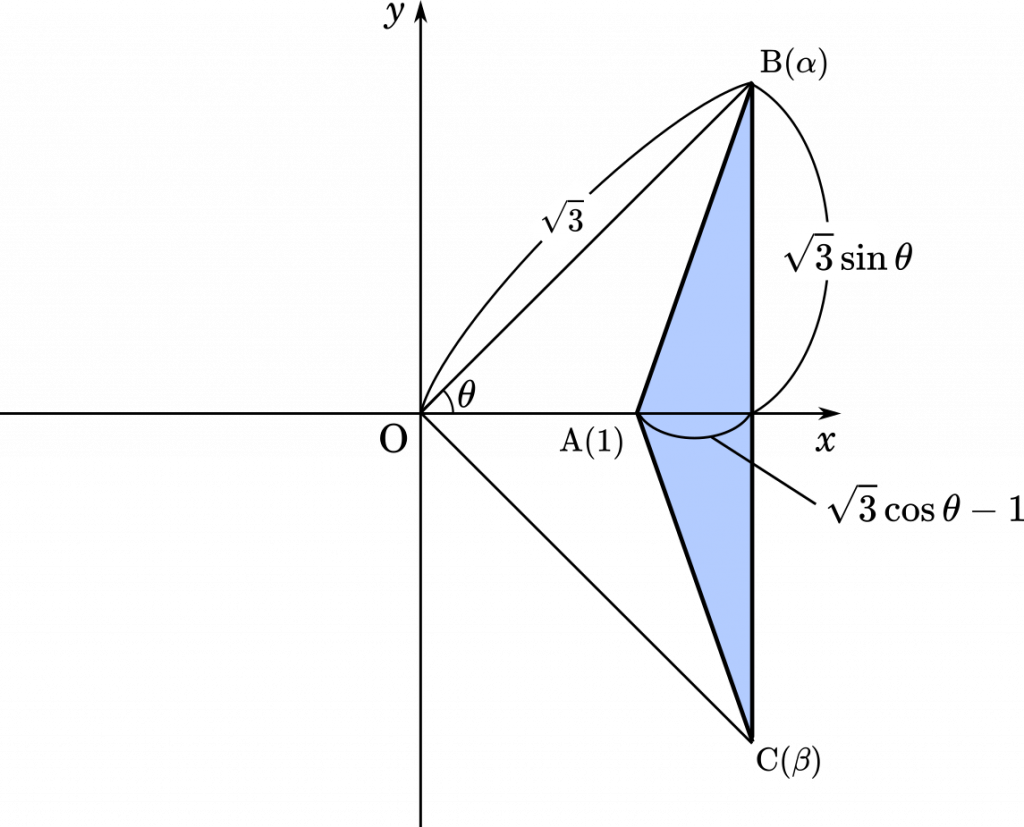
$\alpha$ を極形式で表すと

$\alpha=\sqrt{3}(\cos\theta+i\sin\theta)$

でした。ここから，$\alpha$ の座標が $(\sqrt{3}\cos\theta,\sqrt{3}\sin\theta)$ であることがわかります。

三角形の面積は

$S=2\cdot\cfrac{1}{2}(\sqrt{3}\cos\theta-1)\cdot\sqrt{3}\sin\theta$
$=3\sin\theta\cos\theta-\sqrt{3}\sin\theta$ (答え)

最大値を求める

(3)に進みます。

$g(\theta)=3\sin\theta\cos\theta-\sqrt{3}\sin\theta$

として，$g(\theta)$ の最大値を考えていきます。ここは微分して増減表を作っていきましょう。

$g'(\theta)=3\{(\sin\theta)’\cos\theta+\sin\theta(\cos\theta)’\}-\sqrt{3}\cos\theta$
$=3(\cos^2\theta-\sin^2\theta)-\sqrt{3}\cos\theta$
$=3\{\cos^2\theta-(1-\cos^2\theta)\}-\sqrt{3}\cos\theta$
$=3(2\cos^2-1)-\sqrt{3}\cos\theta$
$=6\cos^2\theta-\sqrt{3}\cos\theta-3$

$6\cos^2\theta-\sqrt{3}\cos\theta-3=0$ とすると
$\cos\theta=\cfrac{\sqrt{3}\pm\sqrt{3+72}}{12}$
$=\cfrac{\sqrt{3}\pm5\sqrt{3}}{12}$
$=\cfrac{\sqrt{3}}{2},-\cfrac{\sqrt{3}}{3}$

$\alpha$ の実部は 1 より大きいので

$\alpha=\sqrt{3}(\cos\theta+i\sin\theta)$ より

$\sqrt{3}\cos\theta>1$

となります。よって

$\cos\theta>\cfrac{1}{\sqrt{3}}$

ここから，先ほどの方程式の解のうち負の方は不適となるので

$\cos\theta=\cfrac{\sqrt{3}}{2}$
$\theta=\cfrac{\pi}{6}$

となります。

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline\theta&0&\cdots&\frac{\pi}{6}&\cdots&(t)\\\hline g'(\theta)&&+&0&-\\\hline g(\theta)&&\nearrow&&\searrow\\\hline\end{array}$

(1)より

$f(x)=x^3-(1+\alpha+\beta)x^2+(\beta+\alpha\beta+\alpha)x-\alpha\beta$

でした。また，$\alpha\beta=3$ であることもわかっています。よって

$f(x)=x^3-(1+\alpha+\beta)x^2+(\alpha+\beta+3)x-3$

次に $\alpha+\beta$ を考えましょう。

$\alpha+\beta=\alpha+\overline{\alpha}$

となるので，これは $\alpha$ の実部を 2 倍したものということになります。

$\alpha=\sqrt{3}\Big(\cos\cfrac{\pi}{6}+i\sin\cfrac{\pi}{6}\Big)$ だから

実部は

$\sqrt{3}\cos\cfrac{\pi}{6}=\sqrt{3}\cdot\cfrac{\sqrt{3}}{2}$
$=\cfrac{3}{2}$

よって，実部の 2 倍は 3 です。

$f(x)=x^3-(1+3)x^2+(3+3)x-3$
$=x^3-4x^2+6x-3$　（答え）