【数IA】外接球の半径を考える(千葉大2012第2問)

四面体の 4 つの頂点がある球面上にあるものを外接球と言います。今回は外接球のイメージをつかみながら球の半径を考えてみます。

余弦定理を用いる

(1)から考えます。
△ABC のそれぞれの辺の長さが分かっているので余弦定理を使います。
$7^2=5^2+8^2-2\cdot5\cdot8\cos$ ∠BAC
$49=25+64-80\cos$ ∠BAC
$80\cos$ ∠BAC $=40$
$\cos$ ∠BAC $=\cfrac{1}{2}$
三角形の内角が 180° を超えることはないので
∠BAC = 60°　（答え）

正弦定理を用いる

(2)に進みます。外接円の半径と言えば正弦定理を使うことを思い出しましょう。
$\cfrac{7}{\sin\angle\text{BAC}}=2R$
∠BAC = 60° より
$\cfrac{7}{\space\cfrac{\sqrt{3}}{2}\space}=2R$
$R=\cfrac{7}{\space2\times\cfrac{\sqrt{3}}{2}\space}$
$=\cfrac{7}{\sqrt{3}}=\cfrac{7\sqrt{3}}{3}$ （答え）

外接球の半径のイメージ

(3)を考えていきます。

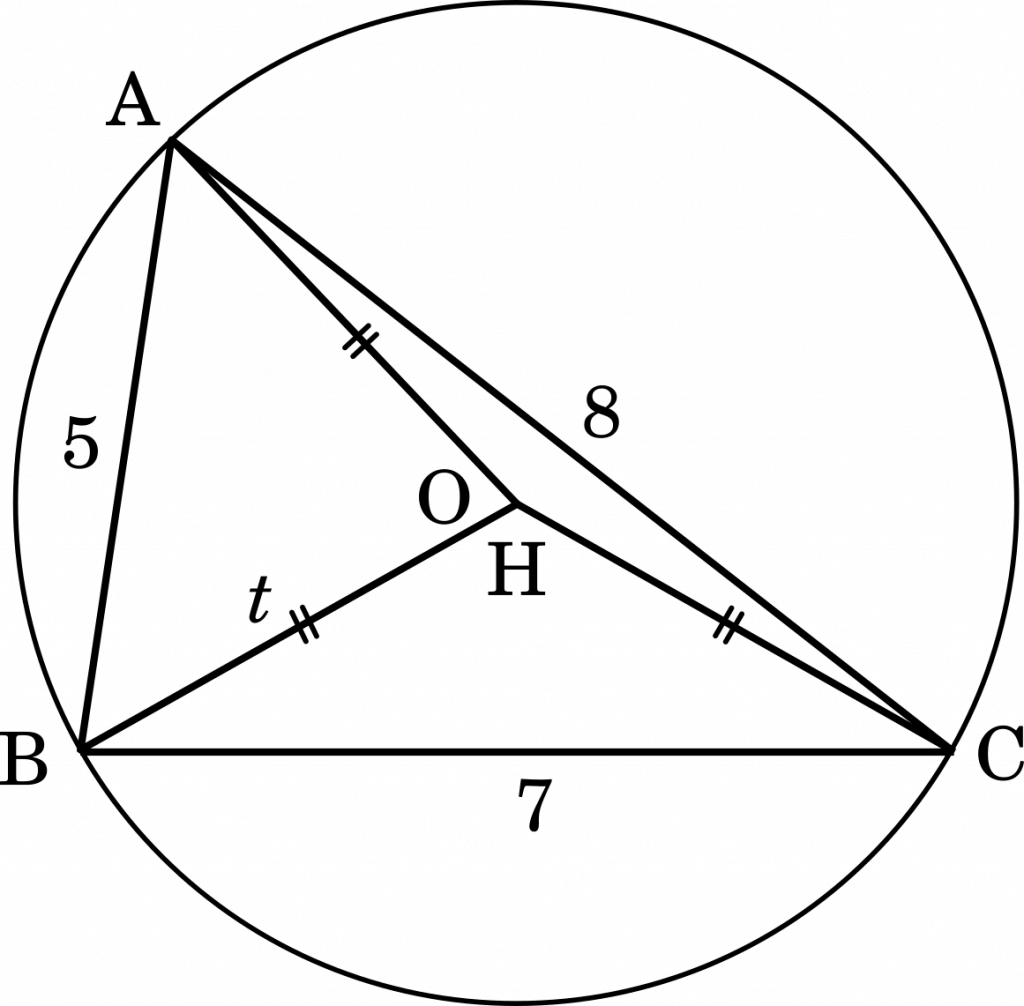
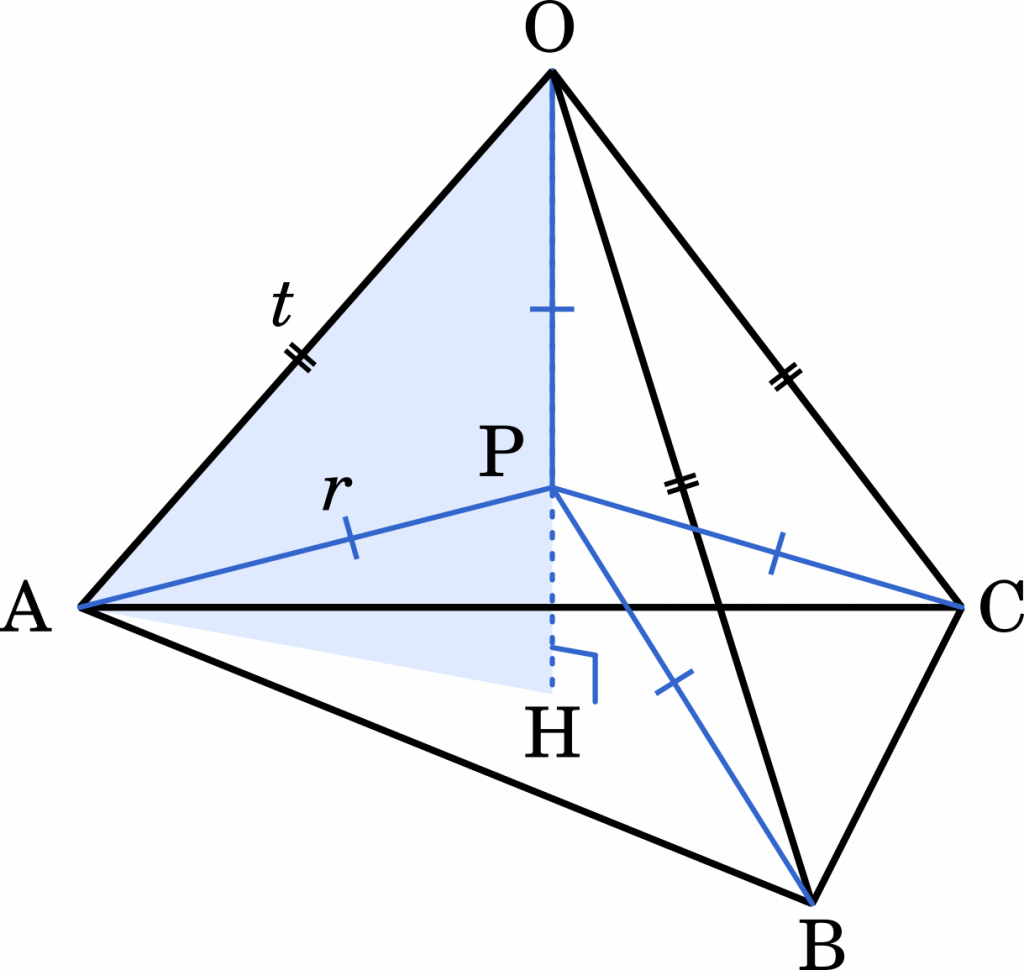
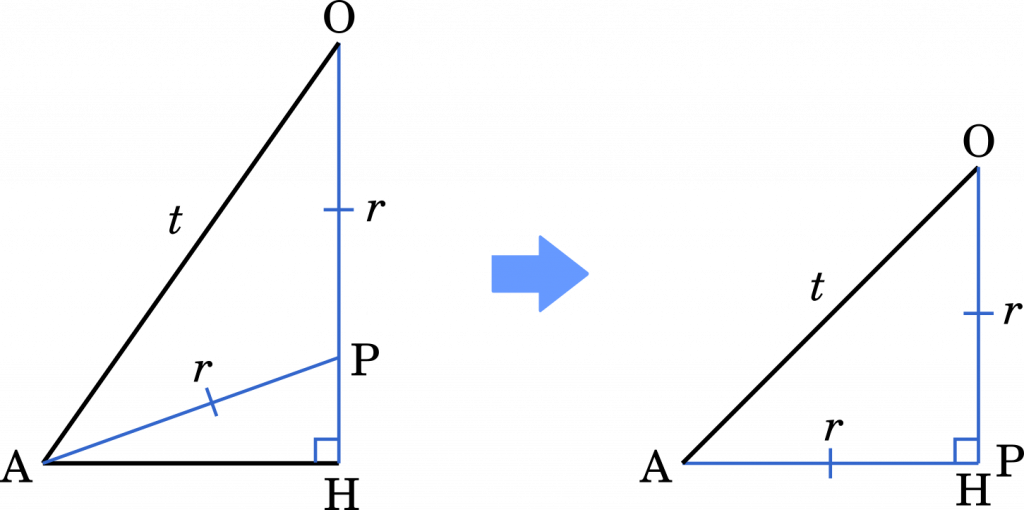
△OAH の部分を見てみます。球の中心を P，半径を $r$ とすると上の図のように表すことができます。そして，$r$ が最も短くなるときを考えると，P と H が一致するときであることが分かります。

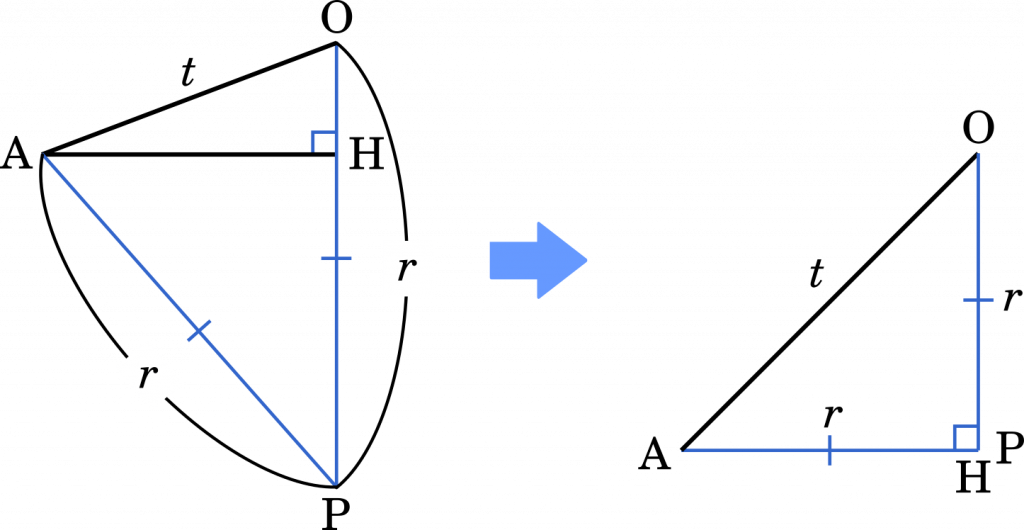
もう１パターンは中心 P が線分 OH の延長線上にあるときです。球の中心が OH の間にあるとは限らないことを念頭に入れておきましょう。
とは言え，今回はどちらも同じ結論になります。
結局，球の半径が最小になるとき，AH に等しくなります。そして AH は △ABC の外接円の半径だから，$\cfrac{7\sqrt{3}}{3}$ です。
あとは $t$ の長さを求めます。△OAH は直角二等辺三角形だから辺の長さの比は $1:1:\sqrt{2}$ です。したがって
$t=\cfrac{7\sqrt{3}}{3}\times\sqrt{2}=\cfrac{7\sqrt{6}}{3}$ （答え）