【数IA二次関数】最小値を場合分け・最小値の最大値(北海道大2018文系第2問)

$a$ と $b$ は実数とし，関数 $f(x)=x^2+ax+b$ の $0\leqq x\leqq1$ における最小値を $m$ とする。

(1) $m$ を $a$ と $b$ で表せ。

(2) $a+2b\leqq2$ を満たす $a$ と $b$ で $m$ を最大にするものを求めよ。また，このときの $m$ の値を求めよ。

(北海道大2018)

平方完成と場合分けを考える

(1)から進めます。

まずは関数がどういうグラフになるかを考えます。そのためにやることと言えば平方完成でした。

$f(x)=x^2+ax+b$ として
$f(x)=\Big(x+\cfrac{a}{2}\Big)^2-\cfrac{a^2}{4}+b$

ここから，場合分けをしていきます。

(i) $-\cfrac{a}{2}<0$ のとき

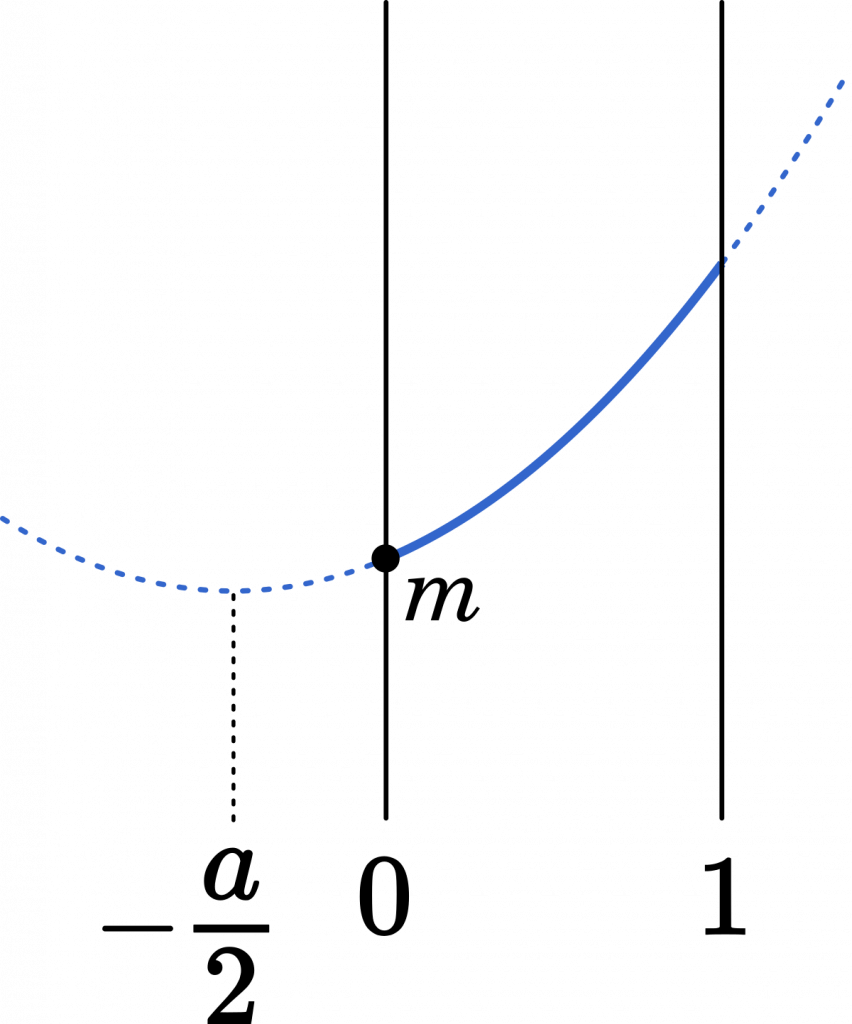
$m=f(0)=b$

(ii) $0\leqq-\cfrac{a}{2}<1$ のとき

$m=f\Big(-\cfrac{a}{2}\Big)=-\cfrac{a^2}{4}+b$

(iii) $1\leqq-\cfrac{a}{2}$ のとき

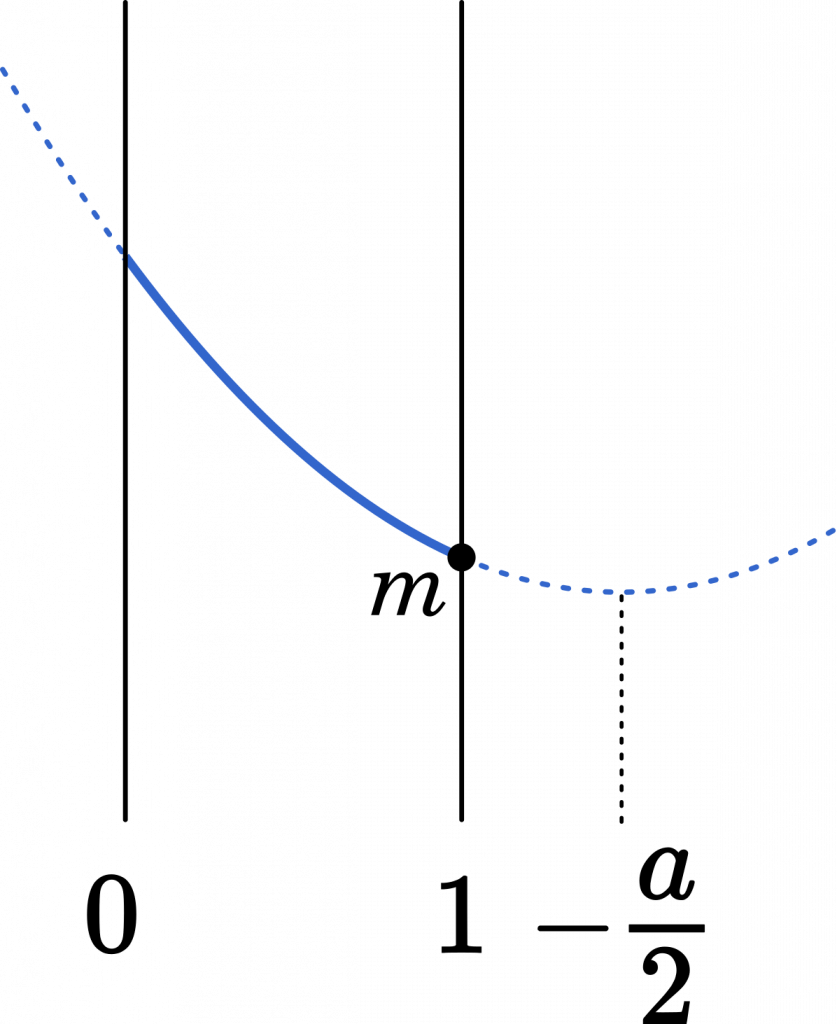
$m=f(1)=a+b+1$

したがって

$\begin{cases}m=b\enspace\Big(-\cfrac{a}{2}<0\text{のとき}\Big)\\m=-\cfrac{a^2}{4}+b\enspace\Big(0\leqq-\cfrac{a}{2}<1\text{のとき}\Big)\\m=a+b+1\enspace\Big(1\leqq-\cfrac{a}{2}\text{のとき}\Big)\end{cases}$

(答え)

a と m のグラフを作る

(2)に進みます。

(i) $-\cfrac{a}{2}<0$ のとき

問題文に不等式があるので，いったんここから $a$ と $b$ についての不等式を作っておきます。
$-\cfrac{a}{2}<0$ より $a>0$
また，$a+2b\leqq2$ より
$2b\leqq-a+2$
$b\leqq-\cfrac{a}{2}+1$
これで，一応 $a$ と $b$ の範囲ができあがります。
さらに $m=b$ だから
$m\leqq-\cfrac{a}{2}+1$
ここから，$m=-\cfrac{a}{2}+1$ のときに $m$ が最大になることは分かりますが，$a$ の値が分からないので，これ以上進めません。

(ii) $0\leqq-\cfrac{a}{2}<1$ のとき

不等式を分けて考えると
$0\leqq-\cfrac{a}{2}$
$a\leqq0$
また
$-\cfrac{a}{2}<1$
$a>-2$
2 つの範囲を合わせると
$-2<a\leqq0$
また，$m=-\cfrac{a^2}{4}+b$ なので，これに式を合わせていきます。
$a+2b\leqq2$ より $b\leqq-\cfrac{a}{2}+1$ だから
$-\cfrac{a^2}{4}+b\leqq-\cfrac{a^2}{4}-\cfrac{a}{2}+1$
$m\leqq-\cfrac{a^2}{4}-\cfrac{a}{2}+1$

一応，$m$ の範囲ができました。次に行きます。

(iii) $1\leqq-\cfrac{a}{2}$ のとき

$1\leqq-\cfrac{a}{2}$
$a\leqq-2$
また，$m=a+b+1$ より
$b\leqq-\cfrac{a}{2}+1$
$a+b+1\leqq-\cfrac{a}{2}+1+a+1$
$a+b+1\leqq-\cfrac{a}{2}+a+2$
$m\leqq-\cfrac{a}{2}+a+2$
$m\leqq\cfrac{a}{2}+2$

できあがった式を整理すると

$\begin{cases}m\leqq-\cfrac{a}{2}\enspace\Big(a>0\text{のとき}\Big)\\m\leqq-\cfrac{a^2}{4}-\cfrac{a}{2}+1\enspace\Big(-2<a\leqq0\text{のとき}\Big)\\m\leqq\cfrac{a}{2}+2\enspace\Big(a\leqq-2\text{のとき}\Big)\end{cases}$

ここで，横軸を $a$，縦軸を $m$ とするグラフを書いてみます。

$m\leqq-\cfrac{a^2}{4}-\cfrac{a}{2}+1$ については平方完成するとよいでしょう。平方完成することでどのようなグラフを書けばよいのかが分かります。

$m=-\cfrac{a^2}{4}-\cfrac{a}{2}+1$ 
$=-\cfrac{1}{4}(a^2+2a)+1$
$=-\cfrac{1}{4}(a+1)^2+\cfrac{1}{4}+1$
$=-\cfrac{1}{4}(a+1)^2+\cfrac{5}{4}$

グラフは

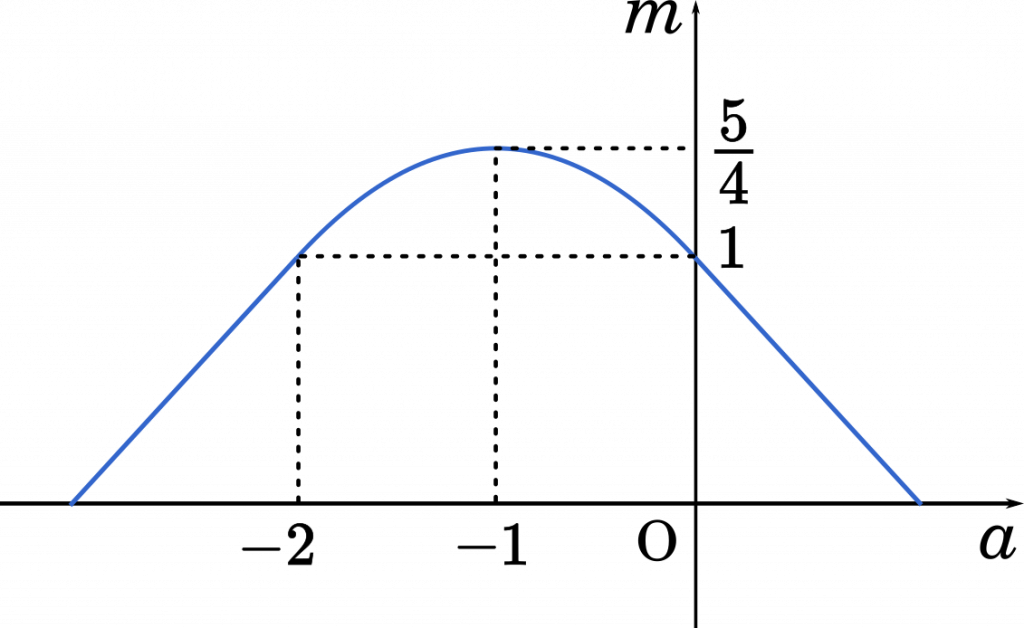
こうして，実際にグラフを作ってみると分かることですが，$m$ は $a=-1$ のときに最大値 $\cfrac{5}{4}$ をとることが分かります。

したがって

$m$ は $a=-1$ のとき，最大値 $\cfrac{5}{4}$ (答え)