二次関数と 2 つの直線で囲まれた図形(横浜国立大2017理系第5問)
正の実数 $a,b$ に対して,連立不等式
$\begin{cases}x\geqq0\\y\geqq x^2\\a^2x^2-(y-b)^2\geqq0\end{cases}$
が表す $xy$ 平面上の領域の面積を $S$ とする。次の問いに答えよ。
(1) $S$ を $a,b$ の式で表せ。
(2) $a,b$ が
$\cfrac{a^2}{4}+\cfrac{4b^2}{9}=1$ $(a,b>0)$
をみたしながら動くとき,$S$ の最大値およびそのときの $a,b$ の値を求めよ。
領域の面積
(1)から始めます。
まずは領域がどこにできるかから考える必要があります。
$a^2x^2-(y-b)^2\geqq0$
$(ax)^2-(y-b)^2\geqq0$
$(ax+y-b)(ax-y+b)\geqq0$
正の数×正の数=正の数,負の数×負の数=正の数です。
不等式が成り立つ条件は
$ax+y-b\geqq0$ かつ $ax-y+b\geqq0$
または
$ax+y-b\leqq0$ かつ $ax-y+b\leqq0$
です。これらを式変形すると
$y\geqq-ax+b$ かつ $y\leqq ax+b$
または
$y\leqq-ax+b$ かつ $y\geqq ax+b$
となります。
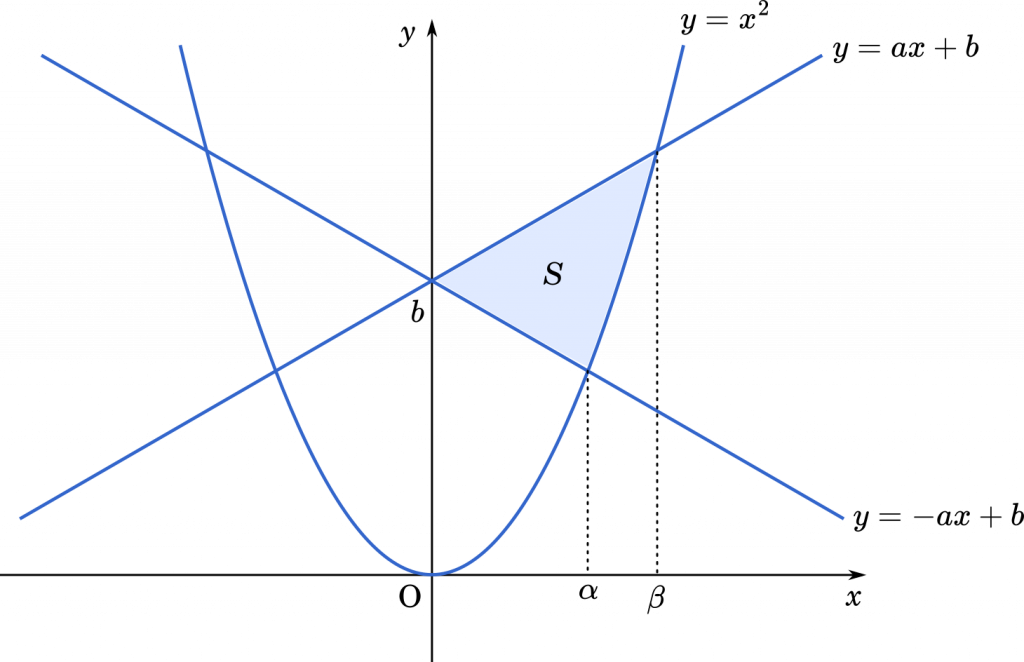
グラフ上で領域を確認してみると
$y\geqq-ax+b$ かつ $y\leqq ax+b$
は領域をつくることができますが
$y\leqq-ax+b$ かつ $y\geqq ax+b$
の場合,$x\geqq0$ の範囲では,2 つの領域はまったく重なりません。したがって,不適です。
よって,領域は上のグラフで示した部分となります。
あとはこれの面積を求めてみましょう。
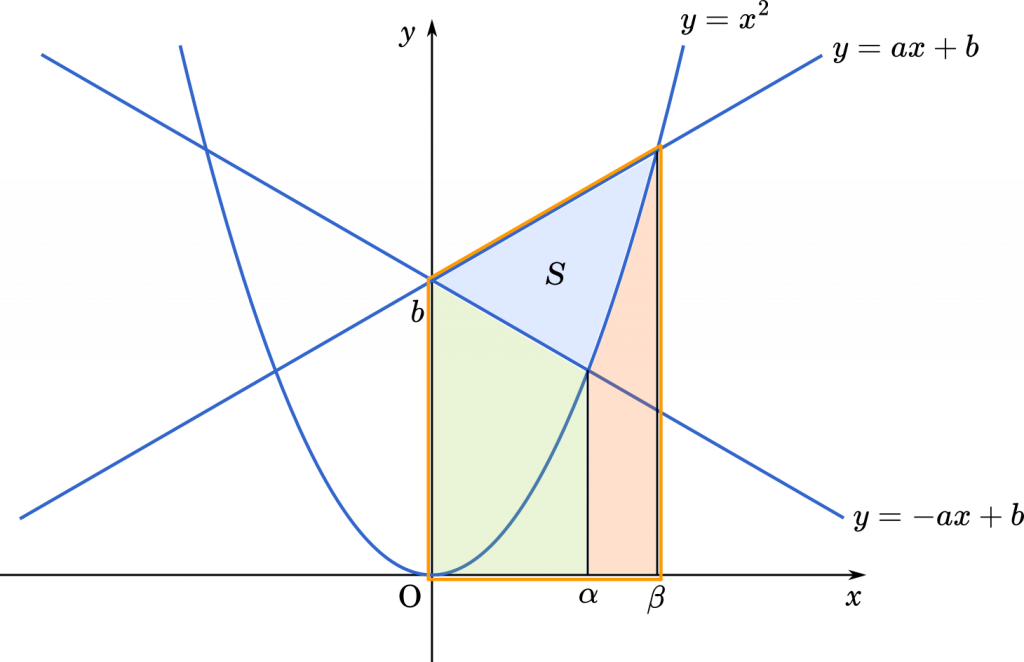
求め方は何通りか考えられますが,今回は台形から緑と赤で示した図形を引いて,残りの青の部分を求めてみます。
$y=x^2$ と $y=-ax+b$ の交点の $x$ 座標を $\alpha$,$y=x^2$ と $y=ax+b$ の交点の$x$ 座標を $\beta$ とすると
$\displaystyle S=\cfrac{1}{2}(b+a\beta+b)\beta-\cfrac{1}{2}(b-a\alpha+b)\alpha-\int_\alpha^\beta x^2\space dx$
$=\cfrac{1}{2}(2b\beta+a\beta^2-2b\alpha+a\alpha^2)-\Big[\cfrac{x^3}{3}\Big]_\alpha^\beta$
$=\cfrac{1}{2}\{2b(\beta-\alpha)+a(\alpha^2+\beta^2)\}-\cfrac{\beta^3-\alpha^3}{3}$
$=b(\beta-\alpha)+\cfrac{a}{2}(\alpha^2+\beta^2)-\cfrac{\beta^3-\alpha^3}{3}$
次に,$\alpha$ と $\beta$ を求めてみましょう。ただし,今回は $\alpha$ と $\beta$ は別々の式から求めるところに注意します。
$y=x^2$ と $y=-ax+b$ を連立して
$x^2+ax-b=0$
$x>0$ より
$x=\cfrac{-a+\sqrt{a^2+4b}}{2}$
また,$y=x^2$ と $y=ax+b$ を連立して
$x^2-ax-b=0$
$x=\cfrac{a+\sqrt{a^2+4b}}{2}$
よって
$\beta-\alpha=a$
解を求めるには,さらに $a^2+b^2$ と $\beta^3-\alpha^3$ が必要なので,これらを求めていきましょう。
$\alpha\beta=\cfrac{-a+\sqrt{a^2+4b}}{2}\cdot\cfrac{a+\sqrt{a^2+4b}}{2}$
$=\cfrac{(\sqrt{a^2+4b})^2-a^2}{4}$
$=b$
これを利用して
$(\beta-\alpha)^2=\alpha^2+\beta^2-2\alpha\beta$
$=\alpha^2+\beta^2-2b$
$a^2=\alpha^2+\beta^2-2b$
$\alpha^2+\beta^2=a^2+2b$
また
$\beta^3-\alpha^3=(\beta-\alpha)(\beta^2+\alpha\beta+\alpha^2)$
$=a(a^2+2b+b)$
$=a(a^2+3b)$
これらを代入して
$S=b\cdot a+\cfrac{a}{2}(a^2+2b)-\cfrac{a(a^2+3b)}{3}$
$=\cfrac{6ab+3a^3+6ab-2a^3-6ab}{6}$
$=\cfrac{1}{6}a^3+ab$ (答え)
楕円の方程式から a,b の範囲を考える
(2)に進みます。
$\cfrac{a^2}{4}+\cfrac{4b^2}{9}=1$ $(a,b>0)$
は,楕円の方程式です。

ここから,$0<a\leqq2$,$0<b\leqq\cfrac{2}{3}$ であることが分かります。この範囲はあとで必要になります。
まず,方程式を変形していきます。
$\cfrac{a^2}{4}+\cfrac{4b^2}{9}=1$
$9a^2+16b^2=36$
$16b^2=36-9a^2$
$16b^2=9(4-a^2)$
$b^2=\cfrac{9}{16}(4-a^2)$
$b>0$ より
$b=\cfrac{3}{4}\sqrt{4-a^2}$
これを $S$ に代入すると
$S=\cfrac{1}{6}a^3+\cfrac{3}{4}a\sqrt{4-a^2}$
ここから最小値を求めていきますが,このままではルートの部分の計算がかなりやっかいなことになります。
そこで,極方程式の考え方を用いてみます。$a$ は横軸方向の値なので,$a=2\cos\theta$ としてみます。
このとき媒介変数の $\theta$ は,$a,b>0$ の条件から,楕円の第1象限である $0<\theta<\cfrac{\pi}{2}$ の範囲で動くことになります。
$\sqrt{4-a^2}=\sqrt{4-4\cos^2\theta}$
$=2\sqrt{1-\cos^2\theta}$
$=2\sin\theta$
これを用いて
$S=\cfrac{1}{6}\cdot8\cos^3\theta+\cfrac{3}{4}\cdot2\cos\theta\cdot2\sin\theta$
$=\cfrac{4}{3}\cos^3\theta+3\sin\theta\cos\theta$
最小値を求めるために,式を微分しましょう。
積の微分
$\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)$
$f(\theta)=\cfrac{4}{3}\cos^3\theta+3\sin\theta\cos\theta$ として
$f'(\theta)=-4\cos^2\theta\sin\theta+3\cos^2\theta-3\sin^2\theta$
$=-4(1-\sin^2\theta)\sin\theta+3(1-\sin^2\theta)-3\sin^2\theta$
$=-4\sin\theta+4\sin^3\theta+3-3\sin^2\theta-3\sin^2\theta$
$=4\sin^3\theta-6\sin^2\theta-4\sin\theta+3$



解の一つを考えるにはコツがあります。$\sin^3\theta$ の係数である 4 と,定数の 3 のそれぞれの約数の組み合わせを作ります。
4 の約数は,1,2,4。3 の約数は 1,3 です。
これをもとに $\cfrac{\textsf{3の約数}}{\textsf{4の約数}}$ を作ります。ただし,今回は第1象限の $\sin\theta$ の値なので,$0<\sin\theta<1$ であることに注意すると
$\cfrac{1}{2},\cfrac{1}{4},\cfrac{3}{4}$
が候補になります。
値を代入してみると $\cfrac{1}{2}$ のときに式が 0 になります。
$4\cdot\cfrac{1}{8}-6\cdot\cfrac{1}{4}-4\cdot\cfrac{1}{2}+3$
$=\cfrac{1}{2}-\cfrac{3}{2}-2+3=0$
解の一つが分かったので,組立除法で因数分解しましょう。
$\begin{matrix}4&-6&-4&3&|\underline{\dfrac{1}{2}}\\&2&-2&-3\\\hline4&-4&-6&0\end{matrix}$
よって
$=\Big(\sin\theta-\cfrac{1}{2}\Big)(4\sin^2\theta-4\sin\theta-6)$
$f(\theta)=0$ のとき,$\sin\theta=\cfrac{1}{2}$ は解の一つです。残り 2 つの解を求めてみます。
$4\sin^2\theta-4\sin\theta-6=0$ とすると
$2\sin^2\theta-2\sin\theta-3=0$
$\sin\theta=\cfrac{1\pm\sqrt{1+6}}{2}$
$=\cfrac{1\pm\sqrt{7}}{2}$
$0<\sin\theta<1$ という条件で考えると,この解は不適です。
よって,解は $\cfrac{1}{2}$ のみです。
増減表は
$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline \theta&(0)&\cdots&\cfrac{\pi}{6}&\cdots&(1)\\\hline f'(\theta)&&+&0&-\\\hline f(\theta)&&\nearrow&&\searrow\\\hline\end{array}$
$a=2\cos\theta$ だったので
$a=2\sqrt{1-\sin^2\theta}$
$=2\sqrt{1-\cfrac{1}{4}}$
$=2\sqrt{\cfrac{3}{4}}$
$=\sqrt{3}$
また
$b=\cfrac{3}{4}\sqrt{4-3}=\cfrac{3}{4}$
となるので
$f(\sqrt{3})=\cfrac{1}{6}\cdot3\sqrt{3}+\sqrt{3}\cdot\cfrac{3}{4}$
$=\cfrac{\sqrt{3}}{2}+\cfrac{3\sqrt{3}}{4}$
$=\cfrac{5\sqrt{3}}{4}$
$a=\sqrt{3}$,$b=\cfrac{3}{4}$ のとき,$S$ は最大値 $\cfrac{5\sqrt{3}}{4}$ をとる。(答え)
SNSでシェア