二次関数と直線の共有点の数（絶対値を含む式）(東京都立大2020文系第3問)

$f(x)=\cfrac{1}{2}|x^2+2x-3|+x-\cfrac{3}{2}$ と定めるとき，以下の問いに答えなさい。

(1) 関数 $y=f(x)$ のグラフをかきなさい。

(2) 曲線 $y=f(x)$ と直線 $y=k(x+3)-\cfrac{5}{2}$ の共有点の個数は，定数 $k$ の値によってどのように変わるか調べなさい。

グラフを描く

(1)から始めます。

$f(x)=\cfrac{1}{2}|x^2+2x-3|+x-\cfrac{3}{2}$

$f(x)=\cfrac{1}{2}|(x+3)(x-1)|+x-\cfrac{3}{2}$

ここで，$y=(x+3)(x-1)$ という二次関数を考えると，$x\leqq-3,x>1$ のとき $y$ は正の値，$-3<x\leqq1$ のとき，負の値になるはずです。

(i) $x\leqq-3,x>1$ のとき

$f(x)=\cfrac{1}{2}(x^2+2x-3)+x-\cfrac{3}{2}$
$=\cfrac{1}{2}x^2+x-\cfrac{3}{2}+x-\cfrac{3}{2}$
$=\cfrac{1}{2}x^2+2x-3$

解答欄の記述はここまででも構いませんが，グラフを描くために関数の頂点が分かった方が描きやすいので，平方完成して頂点を求めておきます。

$=\cfrac{1}{2}(x^2+4x)-3$
$=\cfrac{1}{2}(x+2)^2-2-3$
$=\cfrac{1}{2}(x+2)^2-5$

よって，描くグラフは頂点が $(-2,-5)$ で下に凸の曲線です。

(ii) $-3<x\leqq1$ のとき

絶対値の中はマイナスだから，符号を逆にして絶対値の記号を外しましょう。

$f(x)=\cfrac{1}{2}(-x^2-2x+3)+x-\cfrac{3}{2}$
$=-\cfrac{1}{2}x^2-x+\cfrac{3}{2}+x-\cfrac{3}{2}$
$=-\cfrac{1}{2}x^2$

これは，原点を通り，上に凸の曲線です。

さらに，2つのグラフの交点を求めましょう。

$f(x)=-\cfrac{1}{2}x^2$ より

$f(-3)=-\cfrac{1}{2}(-3)^2=-\cfrac{9}{2}$
$f(1)=-\cfrac{1}{2}\cdot1^2=-\cfrac{1}{2}$

したがって，グラフは

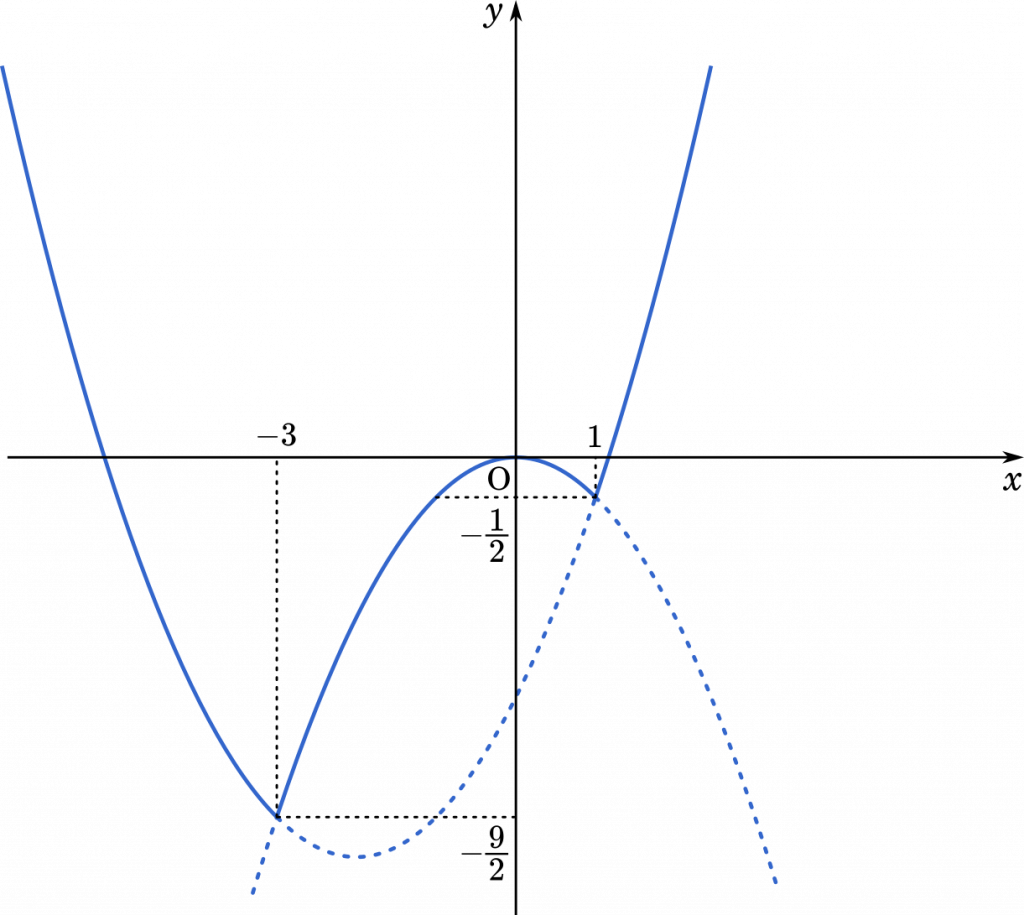
（答え）

共有点の個数を求める

(2)に進みます。

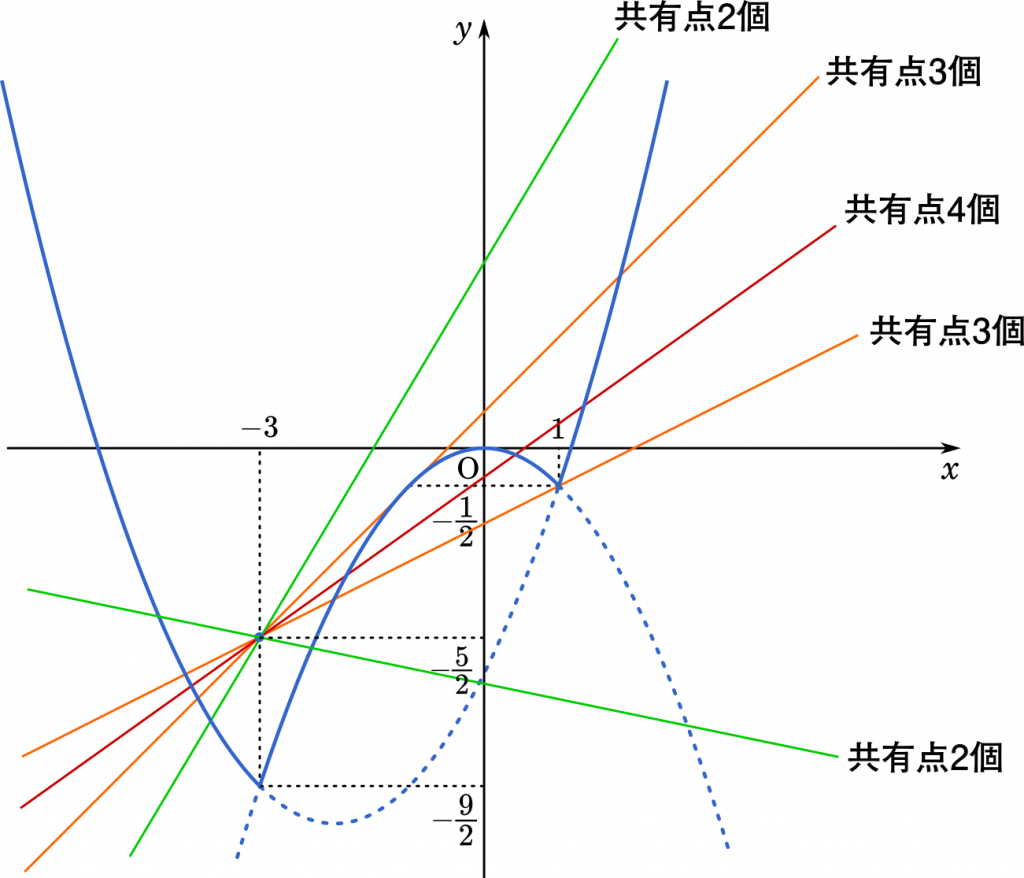
$y=k(x+3)-\cfrac{5}{2}$ に $x=-3$ を代入すると，$y=-\cfrac{5}{2}$ となります。つまり，$k$ の値にかかわらず，式は $\Big(-3,-\cfrac{5}{2}\Big)$ を通ります。

これをもとに，さまざまな直線を引いてみると，共有点が 2 個，3 個，4 個のときがあることが分かります。

共有点が 3 個になるときを調べてみましょう。

$y=k(x+3)-\cfrac{5}{2}$ と $y=-\cfrac{1}{2}x^2$ が共有点を 1 個もつとき，式を連立して

$\cfrac{1}{2}x^2+k(x+3)-\cfrac{5}{2}=0$
$\cfrac{1}{2}x^2+kx+3k-\cfrac{5}{2}=0$
$x^2+2kx+6k-5=0$　・・・①

共有点を 1 個もつとき，判別式は $D=0$ だから

$\cfrac{D}{4}=k^2-6k+5=0$
$(k-1)(k-5)=0$
$k=1,5$

(i) $k=1$ のとき

①に代入して

$x^2+2x+6-5=0$
$x^2+2x+1=0$
$(x+1)^2=0$
$x=-1$

(ii) $k=5$ のとき

①に代入して

$x^2+10x+30-5=0$
$x^2+10x+25=0$
$(x+5)^2=0$
$x=-5$

$-3<x\leqq1$ より $k=1$

これで，$k=1$ のとき，共有点が 3 個できることが分かりました。あともう一つ，3 個の共有点ができるところを考えましょう。

もう一つ，3 個の共有点ができる直線を見てみると，$\Big(1,-\cfrac{1}{2}\Big)$ を通ることが分かります。

$y=k(x+3)-\cfrac{5}{2}$ が，点 $\Big(1,-\cfrac{1}{2}\Big)$ を通るとき

$-\cfrac{1}{2}=k(1+3)-\cfrac{5}{2}$
$4k=2$
$k=\cfrac{1}{2}$

これで，共有点が 3 個のとき，$k=\cfrac{1}{2}$ であることが分かりました。

したがって，共有点の数は

$k<\cfrac{1}{2},\space k>1$ のとき，2 個
$k=\cfrac{1}{2},\space1$ のとき，3 個
$\cfrac{1}{2}<k<1$ のとき，4 個

（答え）