任意の点を通る直線の式・二次関数の最小値（基本レベル）(神戸大2015文系第1問)

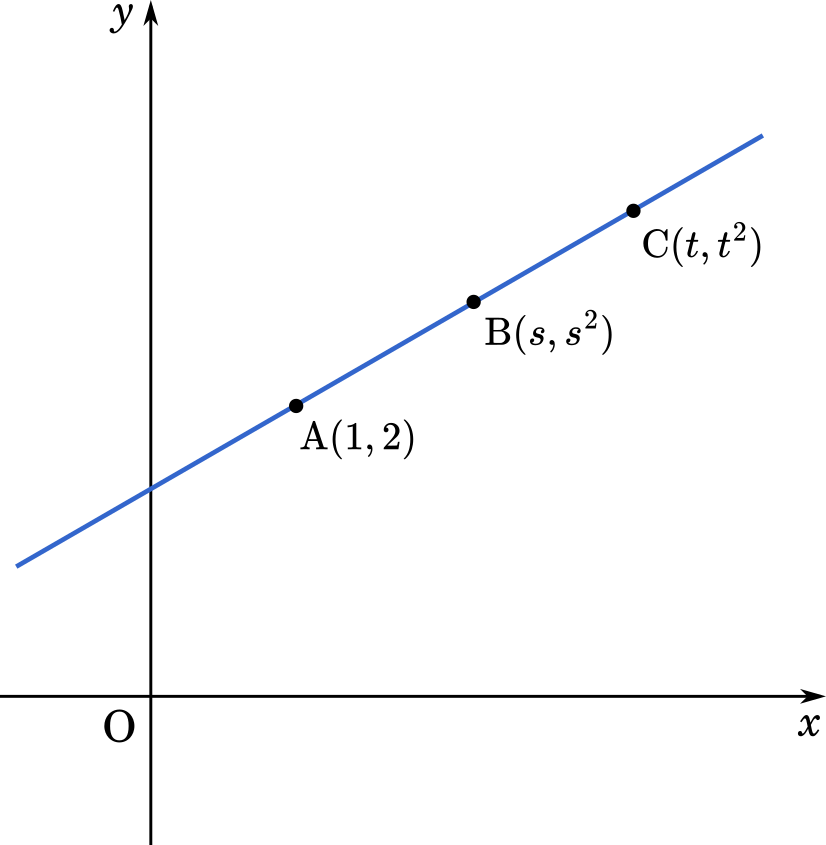
$s,t$ を $s<t$ をみたす実数とする。座標平面上の 3 点 A$(1,2)$，B$(s,s^2)$，C$(t,t^2)$ が一直線上にあるとする。以下の問に答えよ。

(1) $s$ と $t$ の間の関係式を求めよ。

(2) 線分 BC の中点を M$(u,v)$ とする。$u$ と $v$ の間の関係式を求めよ。

(3) $s,t$ が変化するとき，$v$ の最小値と，そのときの $u,s,t$ の値を求めよ。

直線の式

(1)から始めます。

直線の傾きは $\cfrac{y\textsf{の変化量}}{x\textsf{の変化量}}$ で求めます。B と C の座標から $x$ の変化量は $t-s$，$y$ の変化量は $t^2-s^2$ となります。よって，傾きは $\cfrac{t^2-s^2}{t-s}$ です。

$(s,s^2)$ を通り，傾き $\cfrac{t^2-s^2}{t-s}$ の直線の式は

$y-s^2=\cfrac{t^2-s^2}{t-s}(x-s)$
$y-s^2=\cfrac{(t+s)\cancel{(t-s)}}{\cancel{t-s}}(x-s)$
$y-s^2=(t+s)(x-s)$

これが $(1,2)$ を通るので

$2-s^2=(t+s)(1-s)$

もう少し式を整理して答えとします。

$2-s^2=t-st+s-s^2$
$2=s+t-st$　（答え）

中点を求める

(2)に進みます。

まずは，中点の座標を求めましょう。

$(u,v)=\Big(\cfrac{s+t}{2},\cfrac{s^2+t^2}{2}\Big)$

式を変形して

$s+t=2u$　・・・①
$s^2+t^2=2v$　・・・②

②をさらに変形します。

$(s+t)^2-2st=2v$　・・・③

(1)より

$2=s+t-st$
$st=s+t-2$　・・・④

となるので，①と④を③に代入すると

$(2u)^2-2(s+t-2)=2v$
$4u^2-2(2u-2)=2v$
$4u^2-4u+4=2v$
$v=2u^2-2u+2$　（答え）

平方完成して最小値を求める

(3)に進みます。

$v=2u^2-2u+2$

平方完成して最小値を求めましょう。

$v=2(u^2-u)+2$
$=2\Big(u-\cfrac{1}{2}\Big)^2-\cfrac{1}{2}+2$
$=2\Big(u-\cfrac{1}{2}\Big)^2-\cfrac{3}{2}$

よって，$v$ は $u=\cfrac{1}{2}$ のとき最小値 $\cfrac{3}{2}$ をとる。（答え）

$u=\cfrac{1}{2}$ のとき

①に代入して

$s+t=1$　・・・⑤

$v=\cfrac{3}{2}$ を②に代入して

$s^2+t^2=3$　・・・⑥

⑤より

$t=1-s$

⑥に代入して

$s^2+(1-s)^2=3$
$s^2+1-2s+s^2=3$
$2s^2-2s-2=0$
$s^2-s-1=0$
$s=\cfrac{1\pm\sqrt{1+4}}{2}$
$=\cfrac{1\pm\sqrt{5}}{2}$

$s=\cfrac{1+\sqrt{5}}{2}$ のとき

$t=1-\cfrac{1+\sqrt{5}}{2}$
$=\cfrac{1-\sqrt{5}}{2}$

問題文より $s<t$ でした。よって，不適です。

$s=\cfrac{1-\sqrt{5}}{2}$ のとき

$t=1-\cfrac{1-\sqrt{5}}{2}$
$=\cfrac{1+\sqrt{5}}{2}$

よって，適する。したがって

$(s,t)=\Big(\cfrac{1-\sqrt{5}}{2},\cfrac{1+\sqrt{5}}{2}\Big)$　（答え）