【数III複素数平面】複素数と共役な複素数の和は実数であることを利用する(北海道大2016理系第1問)

複素数平面上の点 0 を中心とする半径 2 の円 $C$ 上に点 $z$ がある。$a$ を実数の定数とし，

$$w=z^2-2a+1$$

とおく。(北海道大2016)

(1) $|w|^2$ を $z$ の実部 $x$ と $a$ を用いて表せ。
(2) 点 $z$ が $C$ 上を一周するとき，$|w|$ の最小値を $a$ を用いて表せ。

複素数と共役な複素数の和は実数になる

複素数 $z$ は $z=x+yi$ の形で表すことができます。このとき $x$ を実部，$y$ を虚部と言います。

公式 $z\bar{z}=|z|^2$ を使って，式を変形してみましょう。

$|w|^2=w\bar{w}$ より

$=(z^2-2az+1)(\overline{z^2-2az+1})$
$=(z^2-2ax+1)(\bar{z}^2-2a\bar{z}+1)$

バーは分解できます。例えば

$\overline{2+5i}=\bar{2}+\bar{5}\space\bar{i}$

$i$ のついている部分だけ，符号を反対にします。

$=2+5(-i)=2-5i$

つまり

$\overline{z^2-2az+1}$
$=\bar{z}^2-\overline{2a}\bar{z}+\bar{1}$
$=\bar{z}^2-2a\bar{z}+1$

となります。$z$ は，たとえば $z=1+3i$ のように，その中に実数と虚数を含んでいるので，バーを外すことはできません。反対に，$2a$ や $1$ は虚数の部分を含まない実数なので，符号を変えずにそのままバーを外します。

問題に戻って，式を展開します。

$=z^2\bar{z}^2-2az^2\bar{z}+z^2-2az\bar{z}^2+4a^2z\bar{z}-2az+\bar{z}^2-2a\bar{z}+1$

$z\bar{z}=|z|^2$ より

$=|z|^4-2az|z|^2+z^2-2a\bar{z}|z|^2+4a^2|z|^2-2az+\bar{z}^2-2a\bar{z}+1$

また，$z$ は半径 2 の円周上にあるので

$|z|=2$

が成り立ちます。

$=16-8az+z^2-8a\bar{z}+16a^2-2az+\bar{z}^2-2a\bar{z}+1$
$=z^2+\bar{z}^2-10az-10a\bar{z}+16a^2+17$

最終的に $z$ を消去して，$x$ と $a$ の式にする必要があります。つまり，$z$ の虚部を消去しなければなりません。

そこで，複素数と共役な複素数の和は実数になるという性質を利用します。

$z=x+yi$ とすると
$z+\bar{z}=x+yi+x-yi=2x$

これに，式を合わせていきます。

$(z+\bar{z})^2=z^2+2z\bar{z}+\bar{z}^2$ より
$=(z+\bar{z})^2-2z\bar{z}-10a(z+\bar{z})+16a^2+17$
$z+\bar{z}=2x$ より
$=4x^2-8-20ax+16a^2+17$
$=4x^2-20ax+16a^2+9$ (答え)

絶対値に注意して最小値を求める

(2)に進みます。

(1)より　$|w|^2=4x^2-20ax+16a^2+9$

平方完成すると
$=4(x^2-5ax)+16a^2+9$
$=4\Big(x-\cfrac{5a}{2}\Big)^2-25a^2+16a^2+9$
$=4\Big(x-\cfrac{5a}{2}\Big)^2-9a^2+9$

$z$ は半径 2 の円周上の点であったことに注意します。ここから，$-2\leqq x\leqq 2$ であることが分かるので，場合分けをします。

(i) $\cfrac{5}{2}a\leqq -2$ のとき
$a\leqq -\cfrac{4}{5}$

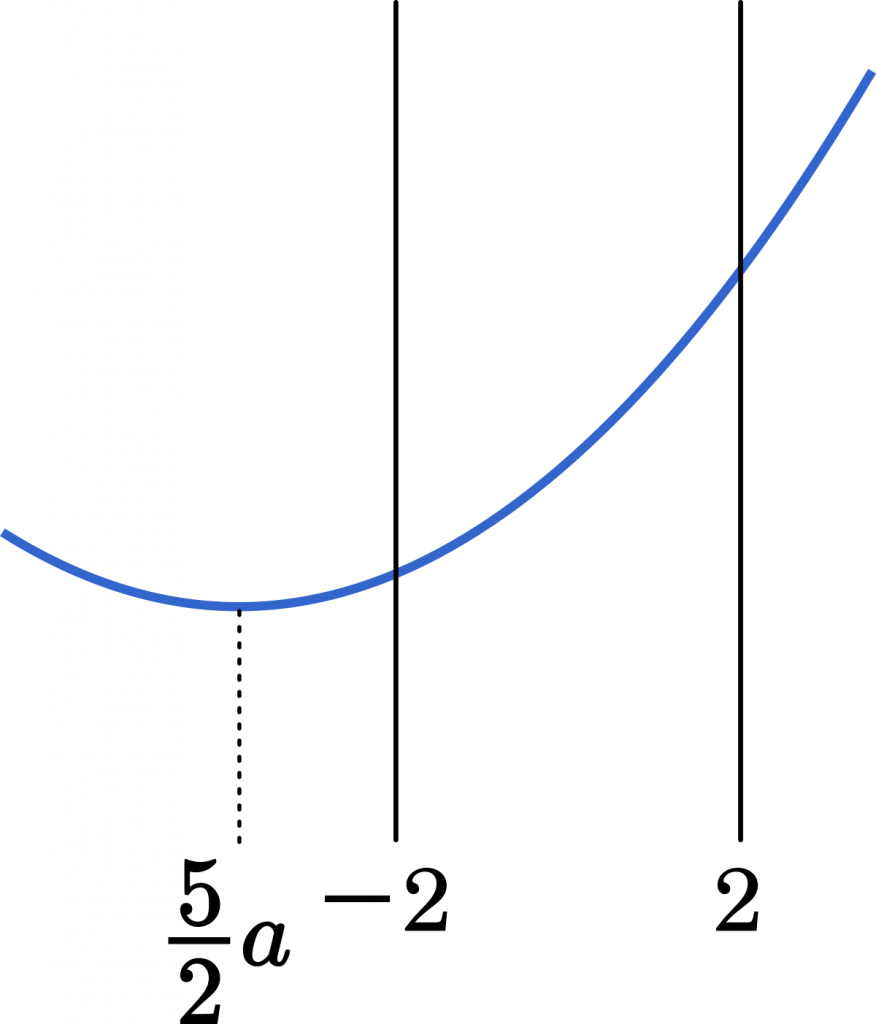
$x=-2$ で最小だから
$|w|^2=4\Big(-2-\cfrac{5a}{2}\Big)^2-9a^2+9$
$=4\Big(4+10a+\cfrac{25a^2}{4}\Big)-9a^2+9$
$=16+40a+25a^2-9a^2+9$
$=16a^2+40a+25$
$=(4a+5)^2$

ここで，$|w|^2$ の 2 乗を外していきますが，右辺に注意します。
$a\leqq-\cfrac{4}{5}$ より，$4a+5$ は負の値になることがあります。しかし，左辺が絶対値であるということは，右辺も必ず正の値にしなければなりません。

したがって
$|w|=|4a+5|$

(ii) $-2<\cfrac{5}{2}a\leqq 2$ のとき
$-\cfrac{4}{5}<a\leqq\cfrac{4}{5}$

$x=\cfrac{5}{2}a$ で最小だから
$|w|^2=-9a^2+9$
$=9(1-a^2)$

したがって
$|w|=|3\sqrt{1-a^2}|$
$1-a^2>0$ だから
$|w|=3\sqrt{1-a^2}$

(iii) $\cfrac{5}{2}a>2$ のとき
$a>\cfrac{4}{5}$

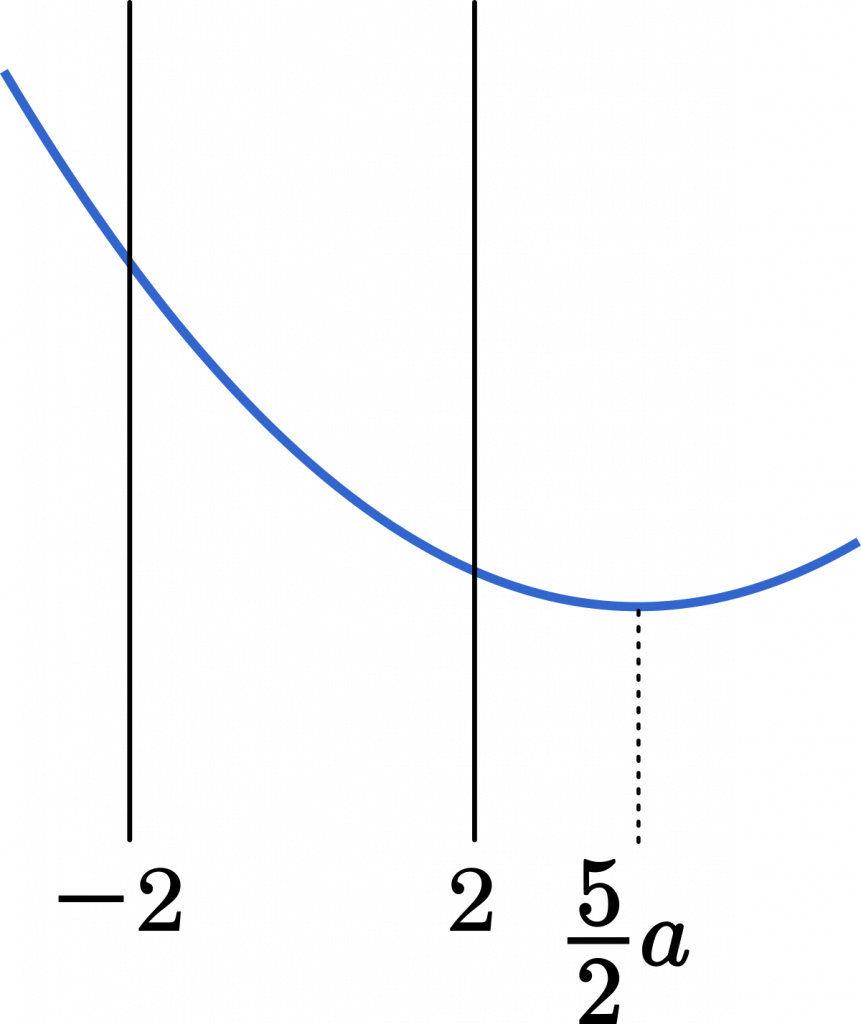
$x=2$ で最小だから
$|w|^2=4\Big(2-\cfrac{5a}{2}\Big)^2-9a^2+9$
$=4\Big(4-10a+\cfrac{25}{4}a^2\Big)-9a^2+9$
$=16-40a+25a^2-9a^2+9$
$=16a^2-40a+25$
$=(4a-5)^2$

したがって
$|w|=|4a-5|$

(答え)
$\begin{cases}|4a+5|\enspace\Big(a\leqq-\cfrac{4}{5}\text{のとき}\Big)\\3\sqrt{1-a^2}\enspace\Big(-\cfrac{4}{5}<a\leqq\cfrac{4}{5}\text{のとき}\Big)\\|4a-5|\enspace\Big(a>\cfrac{4}{5}\text{のとき}\Big)\end{cases}$