【数III微分】接線の座標の存在範囲／漸近線を求めてグラフの概形を描く(九州大2020)

点 $(a,0)$ を通り，曲線 $y=e^{-x}-e^{-2x}$ に接する直線が存在するような定数 $a$ の値の範囲を求めよ。(九州大2020)

問題文から条件を考える

まず，ある曲線に接する直線とは接線のことです。接線の公式を思い出しましょう。

これを用いて，とりあえず接線の式を作ってみましょう。

$f(x)=e^{-x}+e^{-2x}$ として
$f'(x)=-e^{-x}+2e^{-2x}$
$=2e^{-2x}-e^{-x}$

$x=t$ における接線の方程式は
$g(x)=(2e^{-2t}-e^{-t})(x-t)+e^{-t}-e^{-2t}$

これが $(a,0)$ を通るので
$(2e^{-2t}-e^{-t})(a-t)+e^{-t}-e^{-2t}=0$

a を t の関数としてみなす

今までも，例えば二次関数で解が存在するかどうかを考えるときに，$y=ax^2+bx+c$ のような式から判別式 $D$ を作り，$D<0$ なら解が存在しない，という判断をしてきました。

これは $y$ を $x$ の関数とみなして，解の存在範囲を求めているということです。今回も同じように，$a$ を $t$ の関数とみなして，$a$ が存在するかどうかを考えていくことになります。

式を展開して
$(2e^{-2t}-e^{-t})a-(2e^{-2t}-e^{-t})t+e^{-t}-e^{-2t}=0$

$a=\cfrac{(2e^{-2t}-e^{-t})t-e^{-t}+e^{-2t}}{2e^{-2t}-e^{-t}}$
$=\cfrac{2te^{-2t}-te^{-t}-e^{-t}+e^{-2t}}{2e^{-2t}-e^{-t}}$

ここで計算を楽にするために，分母と分子に $e^{2t}$ をかけておきます。

$e^{-2t}\cdot e^{2t}=1$，$e^{-t}\cdot e^{2t}=e^t$ になる。

$=\cfrac{2t-te^t-e^t+1}{2-e^t}$

分母は $2-e^t$ よりは $e^t-2$ の方が一般的な形なので，分母と分子に $-1$ をかけて符号をひっくり返しておきます。

$=\cfrac{te^t+e^t-2t-1}{e^t-2}$

ここから，この関数がどのような形になるか考えます。

ここで，漸近線が引けることに気づけるかどうかが大事なポイントです。分母の $e^t-2$ は 0 になることができません。数学では 0 の割り算はできません。

このとき，$e^t-2=0$ になる $t$ が漸近線になります。漸近線を求めてみましょう。

$e^t-2=0$
$e^t=2$

ここで，対数の定義を思い出しましょう。

これを用いて

$t=\log 2$

底が $e$ のときは式から省略できます。

これで，漸近線の一つが求められました。

$=\cfrac{(e^t-2)+2+te^t-2t-1}{e^t-2}$
$=1+\cfrac{te^t-2t+1}{e^t-2}$

さらに有理化します。

$=1+\cfrac{t(e^t-2)+2t-2t+1}{e^t-2}$
$=t+1+\cfrac{1}{e^t-2}$

ここでもう一つ，$a=t+1$ が漸近線であると言えます。

$t$ の値が大きくなると，$\cfrac{1}{e^t-2}$ は 0 に近づいていきます。つまり，関数のグラフは限りなく $a=t+1$ に近づいていくことになります。これが漸近線です。

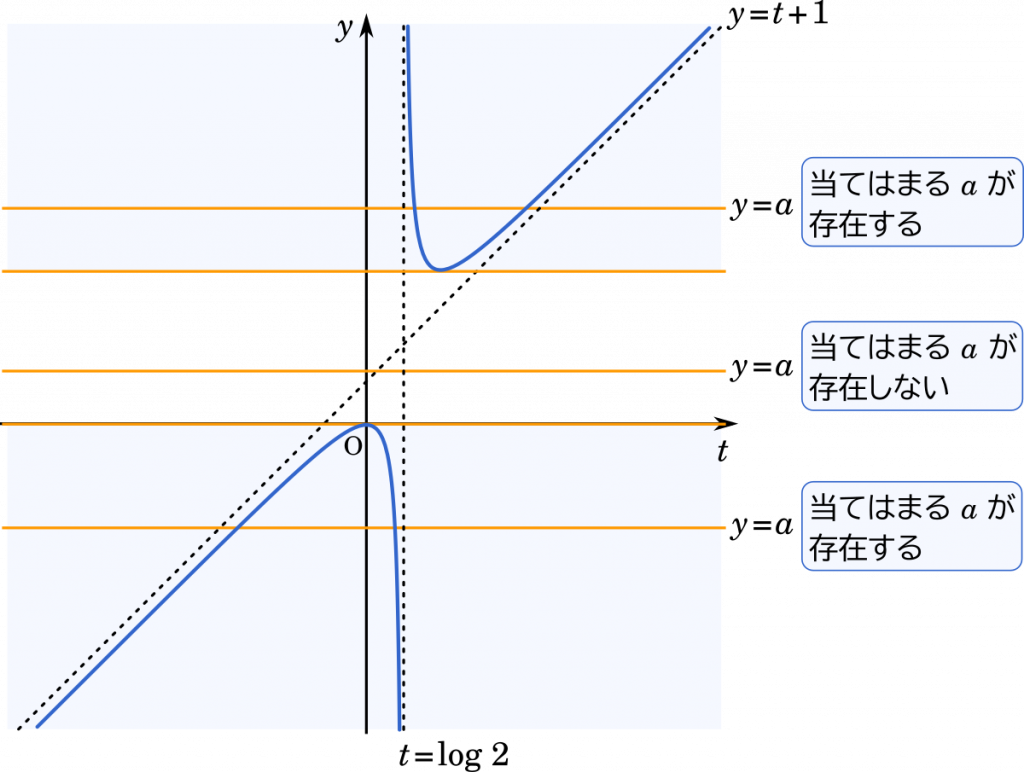
漸近線が描けると，グラフの概形も見えてきます。

あとは，水平な直線を引いて直線と曲線が重なるとき，あてはまる $a$ が存在するということになります。

$g(t)=t+1+\cfrac{1}{e^t-2}$ として

ここで，商の導関数の公式を思い出しましょう。

これを用いて

$g'(t)=1-\cfrac{(e^t-2)’}{(e^t-2)^2}$
$=1-\cfrac{e^t}{(e^t-2)^2}$

$1-\cfrac{e^t}{(e^t-2)^2}=0$ として
$\cfrac{e^t}{(e^t-2)^2}=1$
$e^t=(e^t-2)^2$
$(e^t-2)^2-e^t=0$
$e^{2t}-4e^t+4-e^t=0$
$e^{2t}-5e^t+4=0$
$(e^t-1)(e^t-4)=0$
$e^t=1,4$

$e^t=1$ のとき
$t=0$

$e^t=4$ のとき
$t=\log 4$

よって

$t=0$ のとき
$g(t)=0+1+\cfrac{1}{e^0-2}$
$=1+\cfrac{1}{1-2}=0$

$t=\log 4$ のとき
$g(t)=\log 4+1+\cfrac{1}{e^{\log4}-2}$

ここで，応用として $e^{\log 4}$ の求め方をマスターしましょう。ポイントは，いったん $e^{\log 4}=x$ とおくことです。

$e^{\log4}=x$ として
$\log4=\log x$
$x=4$

すなわち $e^{\log4}=4$

$=\log4+1+\cfrac{1}{2}$
$=\log4+\cfrac{3}{2}$
$\log4=\log2^2=2\log 2$ だから
$=2\log2+\cfrac{3}{2}$

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|c|c|c|}\hline t&\cdots&0&\cdots&\log2&\cdots&\log4&\cdots\\\hline g'(t)&+&0&-&/&-&0&+\\\hline g(t)&\nearrow&&\searrow&/&\searrow&&\nearrow\\\hline\end{array}$

したがって

$a\leqq0,a\geqq2\log2+\cfrac{3}{2}$ (答え)

今回の問題は，接線の式を $a$ と $t$ の関数としてみなすのがポイントです。あとは，教科書通り漸近線を見つけ，グラフの概形を考えていきましょう。