ネイピア数 e の微分積分がわかる！実践問題にチャレンジ(熊本大2021医第3問)

今回はネイピア数 e を使い倒す問題にチャレンジ。問題を解き終えることには e の扱い方が上手になると思うよ。

媒介変数 tt を用いて表された曲線

C:x=12(et+e−t),y=12(et−e−t)C:x=\cfrac{1}{2}(e^t+e^{-t}),y=\cfrac{1}{2}(e^t-e^{-t})

を考える。

(問1) 点 M の座標を (0,1) とする。曲線 CC 上の点 P に対して，MP を最小にする tt の値 t0t_0 を求めよ。

(問2) (問1) の t0t_0 に対する曲線 CC 上の点を Q とする。Q における CC の接線を ℓ\ell とするとき，曲線 CC と接線 ℓ\ell および xx 軸で囲まれた部分 DD の面積を求めよ。

(問3) (問2) の DD を yy 軸の周りに 1 回転させてできる立体の体積を求めよ。

微分して増減表をつくる

(1)から始めます。

MP の長さは三平方の定理で求めることができます。ルートがあると計算がややこしいので MP を 2 乗した値の最小値を考えていきましょう。

f(t)=MP2f(t)=\text{MP}^2 として

={12(et+e−t)}2+{12(et−e−t)−1}2=\Big\{\cfrac{1}{2}(e^t+e^{-t})\Big\}^2+\Big\{\cfrac{1}{2}(e^t-e^{-t})-1\Big\}^2
=14(et+e−t)2+14(et−e−t)2−(et−e−t)+1}=\cfrac{1}{4}(e^t+e^{-t})^2+\cfrac{1}{4}(e^t-e^{-t})^2-(e^t-e^{-t})+1\}

ここで，(et+e−t)2(e^t+e^{-t})^2 は

=e2t+2et⋅e−t+e−2t=e^{2t}+2e^t\cdot e^{-t}+e^{-2t}
=e2t+2et−t+e−2t=e^{2t}+2e^{t-t}+e^{-2t}
=e2t+2e0+e−2t=e^{2t}+2e^0+e^{-2t}
=e2t+2+e−2t=e^{2t}+2+e^{-2t}

となります。

e0=1e^0=1 だからね。

同様にして，(et−e−t)2=e2t−2+e−2t(e^t-e^{-t})^2=e^{2t}-2+e^{-2t} となります。

=14(2e2t+2e−2t)−et+e−t+1=\cfrac{1}{4}(2e^{2t}+2e^{-2t})-e^t+e^{-t}+1
=12e2t+12e−2t−et+e−t+1=\cfrac{1}{2}e^{2t}+\cfrac{1}{2}e^{-2t}-e^t+e^{-t}+1

次に，式を微分しましょう。

ネイピア数の微分
(ex)’=ex(e^x)’=e^x

ネイピア数は微分しても形が同じになるという便利な性質があります。

また，合成関数のときは

(e2x)’=e2x⋅(2x)’=2e2x(e^{2x})’=e^{2x}\cdot(2x)’=2e^{2x}

となります。2x2x を微分した 2 をかけるのを忘れずに。さらに

(e−t)’=e−t⋅(−t)’(e^{-t})’=e^{-t}\cdot(-t)’
=e−t⋅(−1)=−e−t=e^{-t}\cdot(-1)=-e^{-t}

この場合は符号が逆になるから注意して。計算ミスしやすい。

f′(t)=e2t−e−2t−et−e−tf'(t)=e^{2t}-e^{-2t}-e^t-e^{-t}

e2t−e−2t−et−e−t=0e^{2t}-e^{-2t}-e^t-e^{-t}=0 とすると

a2−b2=(a+b)(a−b)a^2-b^2=(a+b)(a-b) の因数分解をする。

(et+e−t)(et−e−t)−(et+e−t)=0(e^t+e^{-t})(e^t-e^{-t})-(e^t+e^{-t})=0
(et+e−t)(et−e−t−1)=0(e^t+e^{-t})(e^t-e^{-t}-1)=0

ここで et+e−t=0e^t+e^{-t}=0 のとき

et+1et=0e^t+\cfrac{1}{e^t}=0

両辺に ete^t をかけて

e2t+1=0e^{2t}+1=0
e2t=−1e^{2t}=-1

ee って 2.7 くらいの正の数だから，何乗しても正の数になる。つまり，この方程式は解なし。

また，et−e−t−1=0e^t-e^{-t}-1=0 のとき

et−1et−1=0e^t-\cfrac{1}{e^t}-1=0

両辺に ete^t をかけて

e2t−1−et=0e^{2t}-1-e^t=0

et=ke^t=k とすると

k2−k−1=0k^2-k-1=0
k=1±1+42k=\cfrac{1\pm\sqrt{1+4}}{2}

kk は正の数だから

=1+52=\cfrac{1+\sqrt{5}}{2}

よって

et=1+52e^t=\cfrac{1+\sqrt{5}}{2}

tt を求めるために，両辺の対数をとります。

log⁡et=log⁡1+52\log e^t=\log\cfrac{1+\sqrt{5}}{2}
tlog⁡e=log⁡1+52t\log e=\log\cfrac{1+\sqrt{5}}{2}

log⁡e\log e はもともと log⁡ee\log_ee ということだった。つまり，log⁡e=1\log e=1 になる。

t=log⁡1+52t=\log\cfrac{1+\sqrt{5}}{2}

増減表は

t⋯log⁡1+52⋯f′(t)−0+f(t)↘↗\def\arraystretch{1.5}\begin{array}{|c||c|c|c|}\hline t&\cdots&\log\frac{1+\sqrt{5}}{2}&\cdots\\\hline f'(t)&-&0&+\\\hline f(t)&\searrow&&\nearrow\\\hline\end{array}

プラス・マイナスの決め方どうしたらいいですか？

たとえば，t=0t=0 とすると，f′(0)=1−1−1−1=−3f'(0)=1-1-1-1=-3 になるのでマイナスです。

また，たとえば t=10t=10 とすると

f′(t)=e2t−e−2t−et−e−tf'(t)=e^{2t}-e^{-2t}-e^t-e^{-t}
=e2t−et−1e2t−1et=e^{2t}-e^t-\cfrac{1}{e^{2t}}-\cfrac{1}{e^t}
=e20−e10−1e20−1e10=e^{20}-e^{10}-\cfrac{1}{e^{20}}-\cfrac{1}{e^{10}}

となります。こうすると，e20e^{20} は e10e^{10} よりはるかに大きな数で，1e20\cfrac{1}{e^{20}} と 1e10\cfrac{1}{e^{10}} は 1 よりもずっと小さい数だから，プラスになります。

この辺りは実際に解答欄に書くわけではないので，頭の中のイメージとして持っておくだけで大丈夫です。

したがって

t0=log⁡1+52t_0=\log\cfrac{1+\sqrt{5}}{2} (答え)

積分で面積を求める

(2)に進みます。

グラフ無いと式が作れない。
概形あった方がイメージしやすいかもね。

グラフの概形を描くために x,yx,y をそれぞれ tt で微分し，増減表を作ります。

x=12(et+e−t)x=\cfrac{1}{2}(e^t+e^{-t})

tt で微分すると

dxdt=12(et−e−t)\cfrac{dx}{dt}=\cfrac{1}{2}(e^t-e^{-t})

et−e−t=0e^t-e^{-t}=0 とすると，t=0t=0 のときに左辺が e0−e−0=1−1=0e^0-e^{-0}=1-1=0 となるので，t=0t=0 で極値をとります。

さらに微分します。

d2xdt2=12(et+e−t)\cfrac{d^2x}{dt^2}=\cfrac{1}{2}(e^t+e^{-t})

et+e−te^t+e^{-t} の場合，ete^t と e−te^{-t} はどちらもつねに正の数で 0 になることはありません。よって，et+e−t=0e^t+e^{-t}=0 としても解はありません。

また

y=12(et−e−t)y=\cfrac{1}{2}(e^t-e^{-t})
dydt=12(et+e−t)\cfrac{dy}{dt}=\cfrac{1}{2}(e^t+e^{-t})
d2ydt2=12(et−e−t)\cfrac{d^2y}{dt^2}=\cfrac{1}{2}(e^t-e^{-t})

増減表は

t⋯0⋯dxdt−0+d2xdt2+e+x1dydt+e+d2ydt2−0+y0\def\arraystretch{1.5}\begin{array}{|c||c|c|c|}\hline t&\cdots&0&\cdots\\\hline \frac{dx}{dt}&-&0&+\\\hline\frac{d^2x}{dt^2}&+&e&+\\\hline x&&1\\\hline\frac{dy}{dt}&+&e&+\\\hline\frac{d^2y}{dt^2}&-&0&+\\\hline y&&0\\\hline\end{array}

まず，接線 ℓ\ell を求めましょう。

傾きどうしたらいいですか？
接線の傾きは dydx\cfrac{dy}{dx} になる。

dydx=dydtdxdt\cfrac{dy}{dx}=\cfrac{\cfrac{dy}{dt}}{\cfrac{dx}{dt}}
=12(et+e−t)12(et−e−t)=\cfrac{\cfrac{1}{2}(e^t+e^{-t})}{\cfrac{1}{2}(e^t-e^{-t})}
=et+e−tet−e−t=\cfrac{e^t+e^{-t}}{e^t-e^{-t}}

t=t0t=t_0 とすると

=et0+e−t0et0−e−t0=\cfrac{e^{t_0}+e^{-t_0}}{e^{t_0}-e^{-t_0}}

ここで，et0e^{t_0} の値を求めてみます。パターンとして覚えましょう。

et0=ke^{t_0}=k として，両辺の対数をとると

log⁡et0=log⁡k\log e^{t_0}=\log k
t0=log⁡kt_0=\log k

log⁡1+52=log⁡k\log\cfrac{1+\sqrt{5}}{2}=\log k
k=1+52k=\cfrac{1+\sqrt{5}}{2}

elog⁡ae^{\log a} みたいな形が来たら，いったん =k=k として両辺の対数を取るってのを覚えておく。

よって

et0=1+52e^{t_0}=\cfrac{1+\sqrt{5}}{2}
=1+52=\cfrac{1+\sqrt{5}}{2}

また

e−t0=21+5e^{-t_0}=\cfrac{2}{1+\sqrt{5}}
=2(1−5)(1+5)(1−5)=\cfrac{2(1-\sqrt{5})}{(1+\sqrt{5})(1-\sqrt{5})}
=2(1−5)−4=\cfrac{2(1-\sqrt{5})}{-4}
=5−12=\cfrac{\sqrt{5}-1}{2}

これらを代入すると

dydx=1+52+5−121+52−5−12\cfrac{dy}{dx}=\cfrac{\cfrac{1+\sqrt{5}}{2}+\cfrac{\sqrt{5}-1}{2}}{\cfrac{1+\sqrt{5}}{2}-\cfrac{\sqrt{5}-1}{2}}
=1+5+5−11+5−5+1=\cfrac{1+\sqrt{5}+\sqrt{5}-1}{1+\sqrt{5}-\sqrt{5}+1}
=252=\cfrac{2\sqrt{5}}{2}
=5=\sqrt{5}

t0t_0 のときの x,yx,y を x0,y0x_0,y_0 とすると，接線 ℓ\ell の方程式は

y=5(x−x0)+y0y=\sqrt{5}(x-x_0)+y_0

となります。x0x_0 と y0y_0 を求めましょう。

x0=12(et0+e−t0)x_0=\cfrac{1}{2}(e^{t_0}+e^{-t_0})
=12(1+52+5−12)=\cfrac{1}{2}\Big(\cfrac{1+\sqrt{5}}{2}+\cfrac{\sqrt{5}-1}{2}\Big)
=52=\cfrac{\sqrt{5}}{2}

y0=12(et0−e−t0)y_0=\cfrac{1}{2}(e^{t_0}-e^{-t_0})
=12(1+52−5−12)=\cfrac{1}{2}\Big(\cfrac{1+\sqrt{5}}{2}-\cfrac{\sqrt{5}-1}{2}\Big)
=12=\cfrac{1}{2}

したがって

ℓ:y=5(x−52)+12\ell:y=\sqrt{5}\Big(x-\cfrac{\sqrt{5}}{2}\Big)+\cfrac{1}{2}
=5x−2=\sqrt{5}x-2

xx 軸との接点を求めます。

5x−2=0\sqrt{5}x-2=0 とすると

x=25=255x=\cfrac{2}{\sqrt{5}}=\cfrac{2\sqrt{5}}{5}

ここから点 Q の座標を (x0,y0)(x_0,y_0) として，面積を求めます。考え方としては三角形の面積から，曲線 CC，x=x0x=x_0 の直線，xx 軸で囲まれた部分を引くと良いでしょう。

三角形の面積は

12(x0−255)⋅y0\cfrac{1}{2}\Big(x_0-\cfrac{2\sqrt{5}}{5}\Big)\cdot y_0

と表すことができます。

=12(52−255)⋅12=\cfrac{1}{2}\Big(\cfrac{\sqrt{5}}{2}-\cfrac{2\sqrt{5}}{5}\Big)\cdot\cfrac{1}{2}
=14⋅55−4510=\cfrac{1}{4}\cdot\cfrac{5\sqrt{5}-4\sqrt{5}}{10}
=540=\cfrac{\sqrt{5}}{40}

また

∫1x0y dx\displaystyle\int_1^{x_0} y\space dx
=∫1x012(et−e−t) dx\displaystyle=\int_1^{x_0}\cfrac{1}{2}(e^t-e^{-t})\space dx
=12∫1x0et−e−t dx\displaystyle=\cfrac{1}{2}\int_1^{x_0}e^t-e^{-t}\space dx

ここ，dtdt じゃないんですか？
dtdt ってしたらダメ。横軸は xx だから dxdx になるよ。
もし dtdt にしたらどうなるんですか？
それは横軸 tt，縦軸 yy のグラフを描いて面積求めることになる。これは増減表作るときに dydt\cfrac{dy}{dt} 求めたからわかると思うけど単調増加のグラフができるから全然別もの。
計算どうなるんですか？
tt の式を xx で積分するってのはできない。こういうときは置換積分するといいよ。

x=12(et+e−t)x=\cfrac{1}{2}(e^t+e^{-t})
dx=12(et−e−t) dtdx=\cfrac{1}{2}(e^t-e^{-t})\space dt

x1→x0t0→t0\def\arraystretch{1.5}\begin{array}{c|c}x&1\rightarrow x_0\\\hline t&0\rightarrow t_0\end{array}

よって

=12∫0t0(et−e−t)⋅12(et−e−t) dt\displaystyle=\cfrac{1}{2}\int_0^{t_0}(e^t-e^{-t})\cdot\cfrac{1}{2}(e^t-e^{-t})\space dt
=14∫0t0(et−e−t)2 dt\displaystyle=\cfrac{1}{4}\int_0^{t_0}(e^t-e^{-t})^2\space dt
=14∫0t0e2t−2+e−2t dt\displaystyle=\cfrac{1}{4}\int_0^{t_0}e^{2t}-2+e^{-2t}\space dt

e2te^{2t} は合成関数だから，積分するとき 2t2t の微分の逆数，つまり 12\cfrac{1}{2} をかけるというルールを思い出して。

=14[12e2t−2t−12e−2t]0t0=\cfrac{1}{4}\Big[\cfrac{1}{2}e^{2t}-2t-\cfrac{1}{2}e^{-2t}\Big]_0^{t_0}
=18[e2t−4t−e−2t]0t0=\cfrac{1}{8}\Big[e^{2t}-4t-e^{-2t}\Big]_0^{t_0}
=18(e2t0−4t0−e−2t0−1+1)=\cfrac{1}{8}(e^{2t_0}-4t_0-e^{-2t_0}-1+1)

ここで，e2t0e^{2t_0} は (et0)2(e^{t_0})^2 と書き換えられる。

(et0)2=(1+52)2(e^{t_0})^2=\Big(\cfrac{1+\sqrt{5}}{2}\Big)^2
=1+25+54=\cfrac{1+2\sqrt{5}+5}{4}
=3+52=\cfrac{3+\sqrt{5}}{2}

また

(e−t0)2=(5−12)2(e^{-t_0})^2=\Big(\cfrac{\sqrt{5}-1}{2}\Big)^2
=5−25+14=\cfrac{5-2\sqrt{5}+1}{4}
=3−52=\cfrac{3-\sqrt{5}}{2}

となるので

=18{3+52−4log⁡1+52−3−52}=\cfrac{1}{8}\Big\{\cfrac{3+\sqrt{5}}{2}-4\log\cfrac{1+\sqrt{5}}{2}-\cfrac{3-\sqrt{5}}{2}\Big\}
=58−12log⁡1+52=\cfrac{\sqrt{5}}{8}-\cfrac{1}{2}\log\cfrac{1+\sqrt{5}}{2}

したがって求める面積は

S=540−58+12log⁡1+52S=\cfrac{\sqrt{5}}{40}-\cfrac{\sqrt{5}}{8}+\cfrac{1}{2}\log\cfrac{1+\sqrt{5}}{2}
S=−510+12log⁡1+52S=-\cfrac{\sqrt{5}}{10}+\cfrac{1}{2}\log\cfrac{1+\sqrt{5}}{2}　（答え）

y 軸の周りに 1 回転させてできる立体の体積

(3)に進みます。

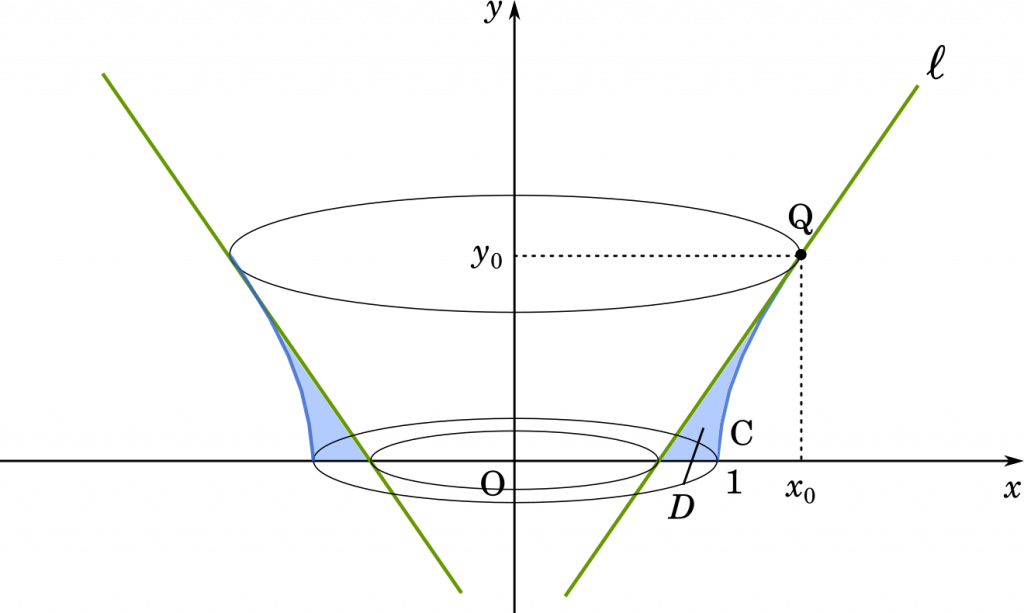
イメージこんな感じ。曲線 CC がつくる回転体は xx 方向が半径になるから，そこから円の面積をつくって積分していく。あと真ん中が空洞になるからその部分の体積をあとから引く。

まず，曲線 CC がつくる回転体の体積を求めましょう。

V1=∫0y0πr2 dy\displaystyle V_1=\int_0^{y_0} \pi r^2\space dy
=π∫0y0{12(et+e−t)}2 dy\displaystyle=\pi\int_0^{y_0}\Big\{\cfrac{1}{2}(e^t+e^{-t})\Big\}^2\space dy
=π4∫0y0e2t+2+e−2t dy\displaystyle=\cfrac{\pi}{4}\int_0^{y_0}e^{2t}+2+e^{-2t}\space dy

ここも置換積分で対処します。

y=12(et−e−t)y=\cfrac{1}{2}(e^t-e^{-t})
dy=12(et+e−t)dtdy=\cfrac{1}{2}(e^t+e^{-t})dt

y0→y0t0→t0\def\arraystretch{1.5}\begin{array}{c|c}y&0\rightarrow y_0\\\hline t&0\rightarrow t_0\end{array}

=π4∫0t0(e2t+2+e−2t)⋅12(et+e−t)dt\displaystyle=\cfrac{\pi}{4}\int_0^{t_0}(e^{2t}+2+e^{-2t})\cdot\cfrac{1}{2}(e^t+e^{-t})dt
=π8∫0t0e3t+et+2et+2e−t+e−t+e−3t dt\displaystyle=\cfrac{\pi}{8}\int_0^{t_0}e^{3t}+e^t+2e^t+2e^{-t}+e^{-t}+e^{-3t}\space dt
=π8∫0t0e3t+3et+3e−t+e−3t dt\displaystyle=\cfrac{\pi}{8}\int_0^{t_0}e^{3t}+3e^t+3e^{-t}+e^{-3t}\space dt
=π8[13e3t+3et−3e−t−13e−3t]0t0=\cfrac{\pi}{8}\Big[\cfrac{1}{3}e^{3t}+3e^t-3e^{-t}-\cfrac{1}{3}e^{-3t}\Big]_0^{t_0}
=π8{13e3t0+3et0−3e−t0−13e−3t0−13−3+3+13}=\cfrac{\pi}{8}\Big\{\cfrac{1}{3}e^{3t_0}+3e^{t_0}-3e^{-t_0}-\cfrac{1}{3}e^{-3t_0}-\cfrac{1}{3}-3+3+\cfrac{1}{3}\Big\}
=π8{13e3t0+3et0−3e−t0−13e−3t0}=\cfrac{\pi}{8}\Big\{\cfrac{1}{3}e^{3t_0}+3e^{t_0}-3e^{-t_0}-\cfrac{1}{3}e^{-3t_0}\Big\}

ここで

e3t0=(et0)3e^{3t_0}=(e^{t_0})^3

さきほど，(et0)2(e^{t_0})^2 を求めたのでそれを利用しましょう。

(et0)3=(et0)2⋅et0(e^{t_0})^3=(e^{t_0})^2\cdot e^{t_0}
=3+52⋅1+52=\cfrac{3+\sqrt{5}}{2}\cdot\cfrac{1+\sqrt{5}}{2}
=3+35+5+54=\cfrac{3+3\sqrt{5}+\sqrt{5}+5}{4}
=2+5=2+\sqrt{5}

また

(e−t0)3=(e−t0)2⋅e−t0(e^{-t_0})^3=(e^{-t_0})^2\cdot e^{-t_0}
=3−52⋅5−12=\cfrac{3-\sqrt{5}}{2}\cdot\cfrac{\sqrt{5}-1}{2}
=35−3−5+54=\cfrac{3\sqrt{5}-3-5+\sqrt{5}}{4}
=5−2=\sqrt{5}-2

となるので

=π8{2+53+3(1+5)2−3(5−1)2−5−23}=\cfrac{\pi}{8}\Big\{\cfrac{2+\sqrt{5}}{3}+\cfrac{3(1+\sqrt{5})}{2}-\cfrac{3(\sqrt{5}-1)}{2}-\cfrac{\sqrt{5}-2}{3}\Big\}
=π8(43+3)=\cfrac{\pi}{8}\Big(\cfrac{4}{3}+3\Big)
=π8⋅133=\cfrac{\pi}{8}\cdot\cfrac{13}{3}
=1324π=\cfrac{13}{24}\pi

次に真ん中の空洞部分の体積を求めましょう。

接線 ℓ\ell の方程式は y=5−2y=\sqrt{5}-2 でした。ただし，ここで必要なのは円の半径を表す xx の値です。

y=5x−2y=\sqrt{5}x-2
x=y+25x=\cfrac{y+2}{\sqrt{5}}

これを円の半径として積分しましょう。

V2=∫0y0πr2 dy\displaystyle V_2=\int_0^{y_0}\pi r^2\space dy
=π∫0y0(y+25)2 dy\displaystyle=\pi\int_0^{y_0}\Big(\cfrac{y+2}{\sqrt{5}}\Big)^2\space dy
=π5∫0y0y2+4y+4 dy\displaystyle=\cfrac{\pi}{5}\int_0^{y_0}y^2+4y+4\space dy
=π5[y33+2y2+4y]0y0\displaystyle=\cfrac{\pi}{5}\Big[\cfrac{y^3}{3}+2y^2+4y\Big]_0^{y_0}
=π5(y033+2y02+4y0)=\cfrac{\pi}{5}\Big(\cfrac{{y_0}^3}{3}+2{y_0}^2+4y_0\Big)

ここで，いっぺん y0=12y_0=\cfrac{1}{2} を求めていたことを思い出して。

=π5(13⋅18+2⋅14+4⋅12)=\cfrac{\pi}{5}\Big(\cfrac{1}{3}\cdot\cfrac{1}{8}+2\cdot\cfrac{1}{4}+4\cdot\cfrac{1}{2}\Big)
=π5(124+12+2)=\cfrac{\pi}{5}\Big(\cfrac{1}{24}+\cfrac{1}{2}+2\Big)
=π5⋅1+12+4824=\cfrac{\pi}{5}\cdot\cfrac{1+12+48}{24}
=61120π=\cfrac{61}{120}\pi

最後に引き算をして体積を求めましょう。

V=V1−V2V=V_1-V_2
=1324π−61120π=\cfrac{13}{24}\pi-\cfrac{61}{120}\pi
=130−122240π=\cfrac{130-122}{240}\pi
=8240π=\cfrac{8}{240}\pi
=130π=\cfrac{1}{30}\pi　（答え）

SNSでシェア

mm参考書 2019-2023