二次関数と接線で囲まれた部分の面積の求めかたの基本(神戸大2019文系第1問)
$a,b,c$ を実数とし,$a\not=0$ とする。2 次関数 $f(x)$ を
$$f(x)=ax^2+bx+c$$
で定める。曲線 $y=f(x)$ は点 $\Big(2,2-\cfrac{c}{2}\Big)$ を通り,
$$\displaystyle\int_0^3f(x)dx=\cfrac{9}{2}$$
をみたすとする。以下の問に答えよ。
(1) 関数 $f(x)$ を $a$ を用いて表わせ。
(2) 点 $(1,f(1))$ における曲線 $y=f(x)$ の接線を $\ell$ とする。直線 $\ell$ の方程式を $a$ を用いて表わせ。
(3) $0<a<\cfrac{1}{2}$ とする。(2)で求めた直線 $\ell$ の $y\geqq0$ の部分と曲線 $y=f(x)$ の $x\geqq0$ の部分および $x$ 軸で囲まれた図形の面積 $S$ の最大値と,そのときの $a$ の値を求めよ。
連立方程式をつくる
(1)から始めます。
手がかりを得るために,とりあえず積分してみましょう。
$\displaystyle\int_0^3ax^2+bx+c\space dx$
$=\Big[\cfrac{a}{3}x^3+\cfrac{b}{2}x^2+cx\Big]_0^3$
$=9a+\cfrac{9}{2}b+3c=\cfrac{9}{2}$
$18a+9b+6c=9$
$6a+3b+2c=3$
$3b+2c=3-6a$ ・・・①
問題文が $a$ を用いて表わせ,となっているということは,$b$ と $c$ は使えないということです。そこで,もう一つ式をつくって連立し,$b$ と $c$ の値を求めると良いでしょう。
$f(x)=ax^2+bx+c$ に $\Big(2,2-\cfrac{c}{2}\Big)$ を代入すると
$2-\cfrac{c}{2}=4a+2b+c$
$4-c=8a+4b+2c$
$4b+3c=4-8a$ ・・・②
①×3 - ②×2
$\begin{aligned}9b+6c&=&9-18a\\-)8b+6c&=&8-16a\\\hline b&=&1-2a\end{aligned}$
①に代入して
$3(1-2a)+2c=3-6a$
$3-6a+2c=3-6a$
$2c=0$
$c=0$
したがって
$f(x)=ax^2+(1-2a)x$ (答え)
接線を求める
(2)に進みます。
式を微分して接線の傾きを求め,接線の式をつくりましょう。
$f(x)=ax^2+(1-2a)x$ として
$f'(x)=2ax+1-2a$
$x=1$ を代入して
$f'(1)=2a+1-2a=1$
よって,接線の傾きは 1 です。
$f(1)=a+1-2a=1-a$ なので,接線は $(1,1-a)$ を通る傾き 1 の直線です。
$\ell:y=1\cdot(x-1)+1-a$
$=x-1+1-a$
$=x-a$ (答え)
面積を求める
(3)に進みます。
$f(x)=ax^2+(1-2a)x$ は原点を通り,次のようなグラフになります。
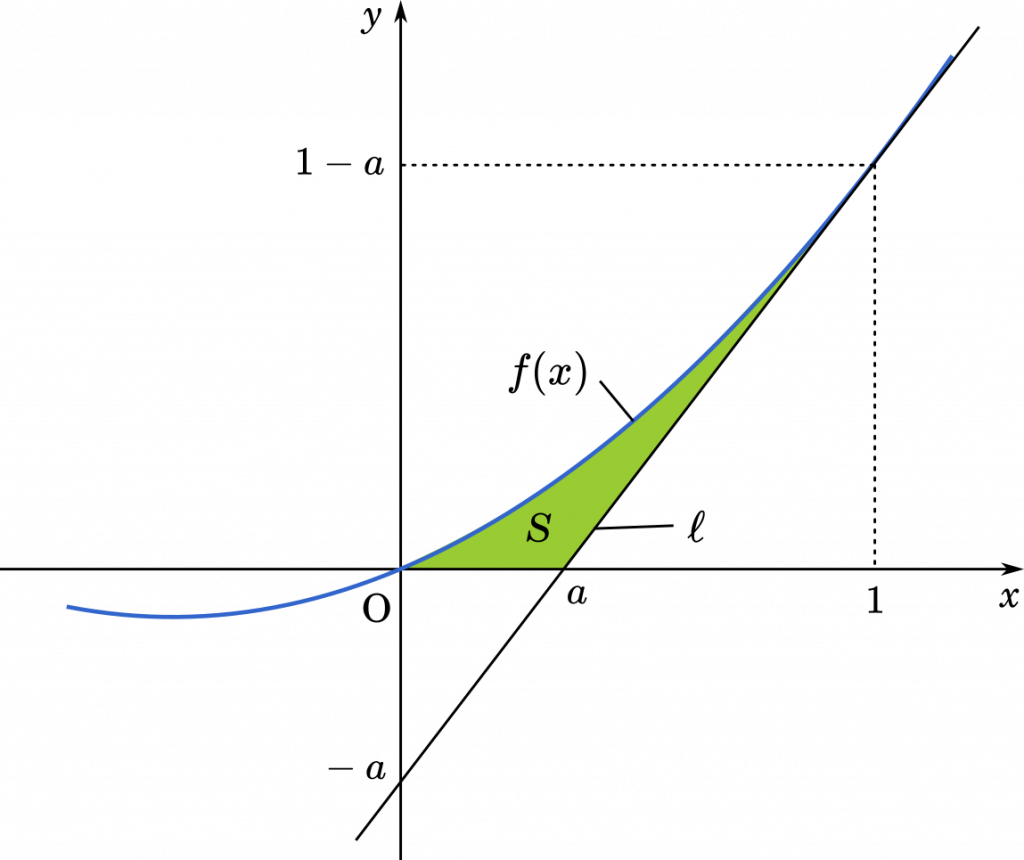
この場合は,$f(x)$ がつくる面積から,三角形の面積を引いたほうがわかりやすいでしょう。
まず,接線と $x$ 軸の交点を求めます。
$x-a=0$ とすると $x=a$
引き算する三角形は底辺が $1-a$ で高さが $1-a$ となるので,面積は $\cfrac{1}{2}(1-a)^2$ となります。
よって,面積は
$\displaystyle S=\int_0^1ax^2+(1-2a)x\space dx-\cfrac{1}{2}(1-a)^2$
$=\Big[\cfrac{a}{3}x^3+\cfrac{1-2a}{2}x^2\Big]_0^1-\cfrac{1}{2}(1-a)^2$
$=\cfrac{a}{3}+\cfrac{1-2a}{2}-\cfrac{1}{2}(1-a)^2$
いったん,分母をまとめて前に出します。
$=\cfrac{1}{6}\{2a+3-6a-3(1-a)^2\}$
$=\cfrac{1}{6}\{-4a+3-3(1-2a+a^2)\}$
$=\cfrac{1}{6}(-4a+3-3+6a-3a^2)$
$=\cfrac{1}{6}(-3a^2+2a)$
$=-\cfrac{1}{2}a^2+\cfrac{1}{3}a$
2 次関数になったので,最大値を求めるために平方完成しましょう。
$=-\cfrac{1}{2}\Big(a^2-\cfrac{2}{3}a\Big)$
$=-\cfrac{1}{2}\Big(a-\cfrac{1}{3}\Big)^2+\cfrac{1}{18}$
したがって
$a=\cfrac{1}{3}$ のとき,最大値は $S=\cfrac{1}{18}$ (答え)
SNSでシェア