【数III積分】円の方程式からつくる回転体の体積（千葉大2020第4問）

領域を求める

$(x^2-2x+y^2)(x^2-3x+y^2)\leqq0$

まずはこの不等式から領域を求める必要があります。

この不等式はカッコを展開してもうまく整理できるわけではないのでこの状態で考えます。

左辺が負の数になるので，正×負＝負または負×正＝負の組合せです。

正×負＝負のパターンを考えてみましょう。

$\begin{cases}x^2-2x+y^2\geqq0\\x^2-3x+y^2<0\end{cases}$

$x^2-2x+y^2\geqq0$

式に $x^2$ と $y^2$ が含まれるものは円の方程式です。$x$ で平方完成すると円の方程式の形になります。

$(x-1)^2-1+y^2\geqq0$
$(x-1)^2+y^2\geqq1$

これは中心の座標が $(1,0)$ で半径が 1 の円です。

$x^2-3x+y^2\leqq0$
$\Big(x-\cfrac{3}{2}\Big)^2-\cfrac{9}{4}+y^2\leqq0$
$\Big(x-\cfrac{3}{2}\Big)^2+y^2\leqq\cfrac{9}{4}$

これは中心の座標が $\Big(\cfrac{3}{2},0\Big)$ で半径が $\cfrac{3}{2}$ の円です。

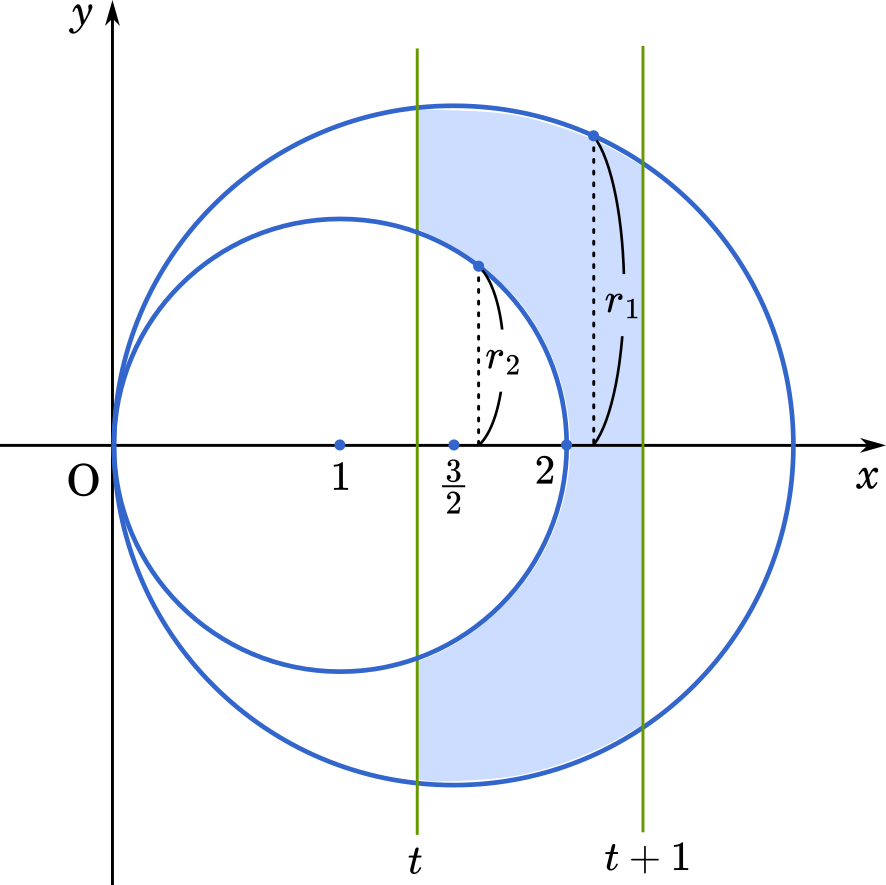
負×正＝負のパターンは上の式の不等号を逆にしたものです。

$(x-1)^2+y^2\leqq1$
$\Big(x-\cfrac{3}{2}\Big)^2+y^2\geqq\cfrac{9}{4}$

この場合，2 つの式を同時に満たす $x,y$ の組合せは存在しません。つまり，不適です。

よって，最初のパターンが正しいことになります。

回転体の体積を求める

$(x-1)^2+y^2\geqq1$
$\Big(x-\cfrac{3}{2}\Big)^2+y^2\leqq\cfrac{9}{4}$

回転体の体積を求めていきましょう。

上の図をもとに式をつくると
$\displaystyle V(t)=\int_t^{t+1}\pi {r_1}^2\space dx-\int_t^2\pi{r_2}^2\space dx$
となります。そして $r_1$ と $r_2$ は
$x^2-3x+y^2=0$ として
$y^2=3x-x^2$
$y=\pm\sqrt{3x-x^2}$
$y$ 座標が半径になるので
$r_1=\sqrt{3x-x^2}$

同様に

$x^2-2x+y^2=0$
$y^2=2x-x^2$
$r_2=\sqrt{2x-x^2}$

これらを代入すると

$\displaystyle V(t)=\pi\int_t^{t+1}3x-x^2\space dx-\pi\int_t^2 2x-x^2\space dx$
$\displaystyle V(t)=\pi\int_t^{t+1}3x-x^2\space dx+\pi\int_t^2 x^2-2x\space dx$

あとは積分を解いていきます。

$=\pi\Big[\cfrac{3}{2}x^2-\cfrac{1}{3}x^3\Big]_t^{t+1}+\pi\Big[\cfrac{1}{3}x^3-x^2\Big]_t^2$
$=\pi\Big\{\cfrac{3}{2}(t+1)^2-\cfrac{1}{3}(t+1)^3-\cfrac{3}{2}t^2+\cfrac{1}{3}t^3\Big\}+\pi\Big\{\cfrac{8}{3}-4-\cfrac{1}{3}t^3+t^2\Big\}$
$=\pi\Big\{\cfrac{3}{2}(t^2+2t+1)-\cfrac{1}{3}(t^3+3t^2+3t+1)-\cfrac{3}{2}t^2+\cfrac{1}{3}t^3-\cfrac{4}{3}-\cfrac{1}{3}t^3+t^2\Big\}$
$=\pi\Big(-\cfrac{1}{3}t^3+2t-\cfrac{1}{6}\Big)$

これで体積が求められました。

体積の最大値

最後に体積の最大値を求めます。微分して増減表をつくりましょう。

$V'(t)=\pi(-t^2+2)$
$-t^2+2=0$ とすると
$t^2=2$
$1\leqq t\leqq2$ より
$t=\sqrt{2}$

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|}\hline t&\cdots&\sqrt{2}&\cdots\\\hline V'(t)&+&0&-\\\hline V(t)&\nearrow&&\searrow\\\hline\end{array}$

$V(\sqrt{2})=\pi\Big(-\cfrac{1}{3}\cdot2\sqrt{2}+2\sqrt{2}-\cfrac{1}{6}\Big)$
$=\pi\Big(\cfrac{4}{3}\sqrt{2}-\cfrac{1}{6}\Big)$　（答え）