【数II軌跡と領域】領域と正方形の面積(東京都立大2018理学部第2問)

$a$，$b$ を $(a,b)\not=(0,0)$ をみたす 0 以上の実数とし，$xy$ 平面上の 2 点 A$(0,a)$ および B$(b,0)$ を頂点とする正方形を ABCD とする。ただし，点 C または点 D は第 1 象限にあるとする。以下の問いに答えなさい。（東京都立大2018）

(1) 点 C，D の座標をそれぞれ求めなさい。また，正方形 ABCD の周および内部が連立不等式
$\begin{cases}0\leqq x\\0\leqq y\\y\leqq-2x+4\end{cases}$
の表す領域に含まれるとき，点$(a,b)$の動く範囲を座標平面上に図示しなさい。

(2) 点$(a,b)$が(1)で求めた範囲を動くとき，正方形 ABCD の面積 $S$ が最大となるような　$(a,b)$ を求めなさい。また，そのときの $S$ の値を求めなさい。

(3) 点$(a,b)$ が(1)の範囲を動き，点 C または点 D のうち少なくとも一方が直線 $y=-2x+4$ の上を動くとき，正方形 ABCD の面積 $S$ が最小となるような $(a,b)$ を求めなさい。また，そのときの $S$ の値を求めなさい。

座標を求める

(1)から始めます。

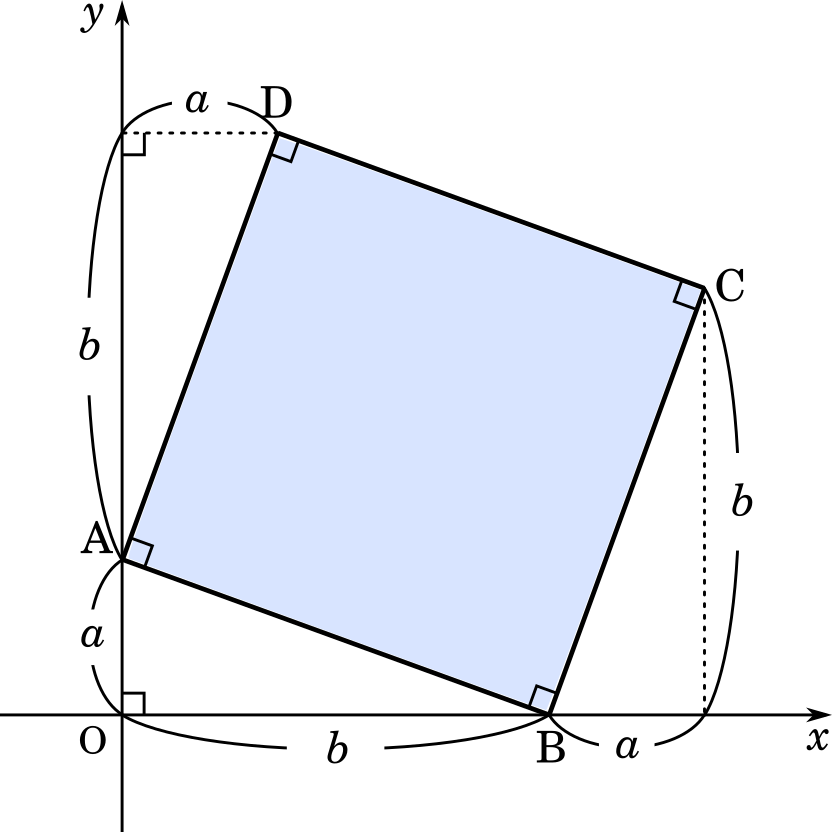
点 C，D の座標は上の図のように考えます。

C$(a+b,b)$，D$(a,a+b)$

次に $a,b$ の範囲を考えていきましょう。

まず，$y=-2x+4$ と $x$ 軸との交点を求めると

$0=-2x+4$
$x=2$

点 A，B の座標が領域のなかに入っていなければならないので

$0\leqq a\leqq4$
$0\leqq b\leqq2$

次に，点 C，D から範囲を考えてみます。

もし，点 C が $y=-2x+4$ の直線上にあるとすると，C の座標を代入して
$b=-2(a+b)+4$
$b=-2a-2b+4$
$3b=-2a+4$
$b=-\cfrac{2}{3}a+\cfrac{4}{3}$

次に点 C が領域の周か内側にあるとすると，その領域は

$y\leqq-2x+4$

となるので，同様に代入すると

$b\leqq-\cfrac{2}{3}a+\cfrac{4}{3}$　・・・①

となります。点 $(a,b)$ の領域は

同様にして，点 D が領域の周か内側にあるとすると，その領域は

$a+b\leqq-2a+4$
$b\leqq-3a+4$　・・・②

①，②を合わせると

交点の座標を求めておきましょう。

$\begin{cases}b=-\cfrac{2}{3}a+\cfrac{4}{3}\\b=-3a+4\end{cases}$

式を連立して

$-\cfrac{2}{3}a+\cfrac{4}{3}=-3a+4$
$-2a+4=-9a+12$
$7a=8$
$a=\cfrac{8}{7}$
$b=-3\cdot\cfrac{8}{7}+4$
$b=\cfrac{-24+28}{7}=\cfrac{4}{7}$

よって，交点の座標は $(a,b)=\Big(\cfrac{8}{7},\space\cfrac{4}{7}\Big)$

円の半径を考える

(2)に進みます。

AB の長さは，三平方の定理より $\sqrt{a^2+b^2}$ です。

よって，正方形の面積は

$S=(\sqrt{a^2+b^2})^2=a^2+b^2$

となります。

これを

$a^2+b^2=S$

と書いてみると，円の方程式を表していることが分かります。

つまり，面積を最大にするということは，円の半径を最大にするということです。ただし，$a$ と $b$ の値が領域のなかに入っていなければなりません。

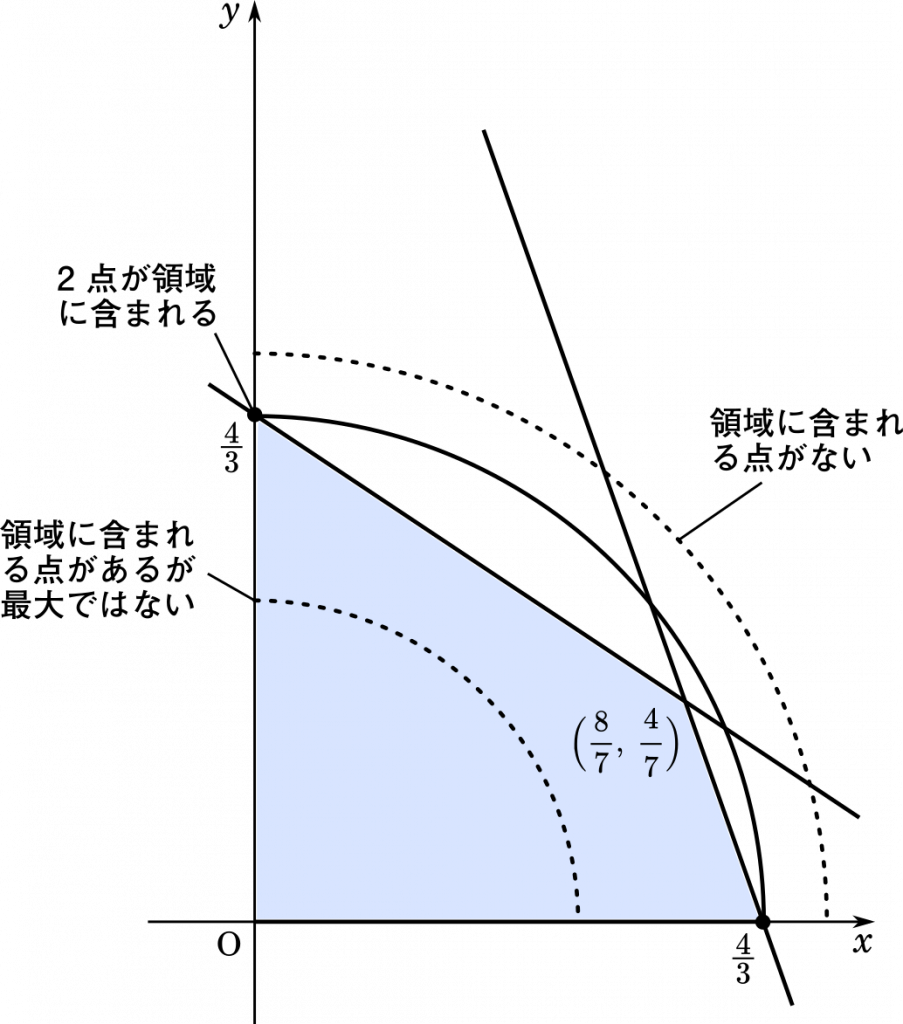
いろいろな半径の円を作ってみると，答えが見えてきます。

円の半径が小さいときには，領域に含まれる点はいくらでもあるのですが，最大ではありません。

半径を大きくしていくと，$\Big(0,\cfrac{4}{3}\Big)$ と $\Big(\cfrac{4}{3},0\Big)$を通る円はこの 2 か所で領域と交わります。これが，半径最大の状態です。

ちなみに，さらに半径を大きくすると，円が領域のなかを通らないので，あてはまる $a$，$b$ は存在しないということになります。

また，きちんとした答えを出すためには，点 $\Big(\cfrac{8}{7},\space\cfrac{4}{7}\Big)$ が最大ではないことを示しておく必要があります。解答の途中に次の記述を入れましょう。

点 $\Big(\cfrac{8}{7},\space\cfrac{4}{7}\Big)$ における面積 $S$ は

$S=a^2+b^2$ に代入して

$S=\Big(\cfrac{8}{7}\Big)^2+\Big(\cfrac{4}{7}\Big)^2=\cfrac{64+16}{49}$
$=\cfrac{80}{49}$

また

$(a,b)=\Big(0,\cfrac{4}{3}\Big)$ または $\Big(\cfrac{4}{3},0\Big)$ のとき

$S=\Big(\cfrac{4}{3}\Big)^2=\cfrac{16}{9}$

$\cfrac{80}{49}$ と $\cfrac{16}{9}$ を比べると

$\cfrac{720}{441}<\cfrac{784}{441}$

よって，$S$ が最大となるのは

$(a,b)=\Big(0,\cfrac{4}{3}\Big)$ または $\Big(\cfrac{4}{3},0\Big)$ のとき

$S=\cfrac{16}{9}$

（答え）

面積の最小

(3)に進みます。ここは，いろいろと考え方があるのですが，強引に計算力で突破する方針で答えを求めてみます。

(i) 点 C が $y=2x+4$ 上を動くとき，(1)より

$b=-\cfrac{2}{3}a+\cfrac{4}{3}$

これを $S=a^2+b^2$ に代入すると

$S=a^2+\Big(-\cfrac{2}{3}a+\cfrac{4}{3}\Big)^2$
$=a^2+\cfrac{4}{9}a^2-\cfrac{16}{9}a+\cfrac{16}{9}$
$=\cfrac{13}{9}a^2-\cfrac{16}{9}a+\cfrac{16}{9}$

これを平方完成していきます。

$=\cfrac{13}{9}\Big(a^2-\cfrac{16}{13}a\Big)+\cfrac{16}{9}$
$=\cfrac{13}{9}\Big(a-\cfrac{8}{13}\Big)^2-\cfrac{13}{9}\cdot\cfrac{8^2}{13^2}+\cfrac{16}{9}$
$=\cfrac{13}{9}\Big(a-\cfrac{8}{13}\Big)^2-\cfrac{1}{9}\cdot\cfrac{8^2}{13}+\cfrac{16}{9}$
$=\cfrac{13}{9}\Big(a-\cfrac{8}{13}\Big)^2+\cfrac{-64+16\cdot13}{9\cdot13}$
$=\cfrac{13}{9}\Big(a-\cfrac{8}{13}\Big)^2+\cfrac{144}{9\cdot13}$
$=\cfrac{13}{9}\Big(a-\cfrac{8}{13}\Big)^2+\cfrac{16}{13}$

よって，最小値は $\cfrac{16}{13}$ です。

また，$a=\cfrac{8}{13}$ のとき $b$ は

$b=-\cfrac{2}{3}\cdot\cfrac{8}{13}+\cfrac{4}{3}$
$=\cfrac{-16+4\cdot13}{3\cdot13}$
$=\cfrac{36}{3\cdot13}=\cfrac{12}{13}$

(ii) 点 D が $y=-2x+4$ 上を動くとき

$b=-3a+4$

$S=a^2+b^2$ に代入すると

$S=a^2+(-3a+4)^2$
$=a^2+9a^2-24a+16$
$=10a^2-24a+16$

平方完成して

$=10\Big(a^2-\cfrac{12}{5}a\Big)+16$
$=10\Big(a-\cfrac{6}{5}\Big)^2-10\cdot\cfrac{36}{25}+16$
$=10\Big(a-\cfrac{6}{5}\Big)^2-2\cdot\cfrac{36}{5}+16$
$=10\Big(a-\cfrac{6}{5}\Big)^2+\cfrac{-72+80}{5}$
$=10\Big(a-\cfrac{6}{5}\Big)^2+\cfrac{8}{5}$

最小値は $\cfrac{8}{5}$ です。このとき $b$ を求めると

$b=-3\cdot\cfrac{6}{5}+4$
$=\cfrac{-18+20}{5}=\cfrac{2}{5}$

$\cfrac{16}{13}$ と $\cfrac{8}{5}$ を比べると

$\cfrac{80}{65}<\cfrac{104}{65}$

したがって，$S$ の最小値は

$(a,b)=\Big(\cfrac{8}{13},\space\cfrac{12}{13}\Big)$ のとき
$S=\cfrac{16}{13}$　（答え）