【数IIBベクトル】三角比の性質を用いて辺の長さを求める(北海道大2021理系第1問)
三角形 OAB において,辺 AB を 2:1 に内分する点を D とし,直線 OA に関して点 D と対称な点を E とする。
$\overrightarrow{\text{OA}}=\vec{a},\overrightarrow{\text{OB}}=\vec{b}$ とし,$|\vec{a}|=4,\vec{a}\cdot\vec{b}=6$ を満たすとする。(北海道大2021)
(1) 点 B から直線 OA に下した垂線と直線 OA との交点を F とする。$\overrightarrow{\text{OF}}$ を $\vec{a}$ を用いて表せ。
(2) $\overrightarrow{\text{OE}}$ を $\vec{a},\vec{b}$ を用いて表せ。
(3) 三角形 BDE の面積が $\cfrac{5}{9}$ になるとき,$|\vec{b}|$ の値を求めよ。
三角比の性質を用いて OF を求める
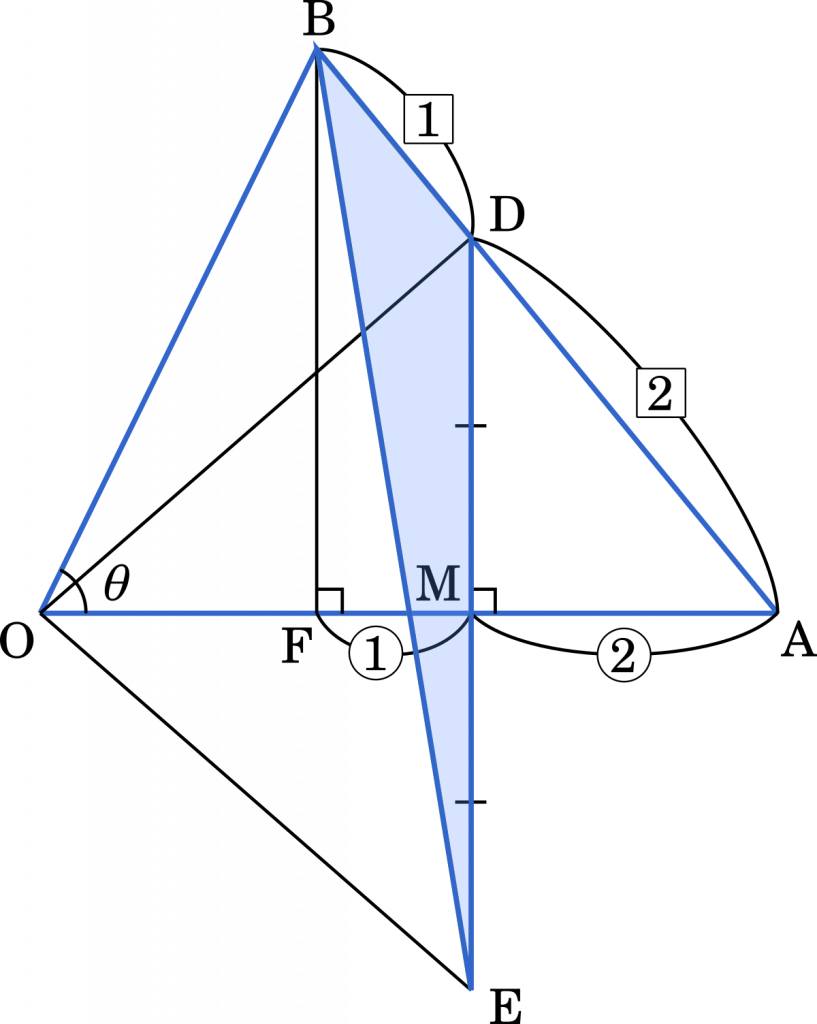
(1)から進めます。
$\angle\text{BOF}=\theta$ として,三角比を用いると
$\cfrac{\text{OF}}{\text{OB}}=\cos\theta$
と表すことができます。これを変形して
$\text{OF}=\text{OB}\cos\theta$
$=|\vec{b}|\cos\theta$ ・・・①
$\cos\theta$ が出てくることから,内積の公式を使うとうまくいきそうです。
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$ より
$=4|\vec{b}|\cos\theta=6$
$|\vec{b}|\cos\theta=\cfrac{3}{2}$
①に代入して
$\text{OF}=\cfrac{3}{2}$
$k$ を実数として
$\text{OF}=\cfrac{3}{2}=k|\vec{a}|$
とすると
$\cfrac{3}{2}=k\cdot4$
$k=\cfrac{3}{8}$
したがって $\text{OF}=\cfrac{3}{8}\vec{a}$ (答え)
中点を利用する
(2)に進みます。
点 E は,直線 OA に関して点 D と対称な点であることから,とりあえず $\overrightarrow{\text{OD}}$ を求めてみましょう。
点 D は辺 AB を 2:1 に内分する点だから
$\overrightarrow{\text{OD}}=\cfrac{\vec{a}+2\vec{b}}{3}$
$=\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}$
次に,辺 DE の中点を M とおくと
$\overrightarrow{\text{OM}}=\cfrac{\overrightarrow{\text{OD}}+\overrightarrow{\text{OE}}}{2}$ ・・・②
となります。ここから,$\overrightarrow{\text{OM}}$ が分かれば,$\overrightarrow{\text{OE}}$ が求められそうです。
BF // DM だから,△ADM∽△ABF です。よって,AM : FM = 2 : 1 となります。
$\text{OF}=\cfrac{3}{2}$ より
$\text{AF}=4-\cfrac{3}{2}=\cfrac{5}{2}$
$\text{FM}=\cfrac{5}{2}\cdot\cfrac{1}{3}=\cfrac{5}{6}$
よって
$\text{OM}=\cfrac{3}{2}+\cfrac{5}{6}$
$=\cfrac{9+5}{6}=\cfrac{14}{6}$
$\text{OM}:\text{OA}=\cfrac{14}{6}:4$
$=7:12$
$\overrightarrow{\text{OM}}=\cfrac{7}{12}\vec{a}$
②を変形して
$\overrightarrow{\text{OM}}=\cfrac{\overrightarrow{\text{OD}}+\overrightarrow{\text{OE}}}{2}$
$2\overrightarrow{\text{OM}}=\overrightarrow{\text{OD}}+\overrightarrow{\text{OE}}$
$\overrightarrow{\text{OE}}=2\overrightarrow{\text{OM}}-\overrightarrow{\text{OD}}$
$=2\cdot\cfrac{7}{12}\vec{a}-\cfrac{1}{3}\vec{a}-\cfrac{2}{3}\vec{b}$
$=\cfrac{5}{6}\vec{a}-\cfrac{2}{3}\vec{b}$ ・・・(答え)
辺の比を用いて三角形の面積を求める
(3)に進みます。
△BDF の面積を求めるには,DE を底辺,FM を高さとして考えれば良さそうです。
$\overrightarrow{\text{DE}}=\overrightarrow{\text{OE}}-\overrightarrow{\text{OD}}$ より
$=\cfrac{5}{6}\vec{a}-\cfrac{2}{3}\vec{b}-\cfrac{1}{3}\vec{a}-\cfrac{2}{3}\vec{b}$
$=\cfrac{1}{2}\vec{a}-\cfrac{4}{3}\vec{b}$
$|\overrightarrow{\text{DE}}|^2=\Big(\cfrac{1}{2}\vec{a}-\cfrac{4}{3}\vec{b}\Big)^2$
$=\cfrac{1}{4}|\vec{a}|^2-\cfrac{4}{3}\vec{a}\cdot\vec{b}+\cfrac{16}{9}|\vec{b}|^2$
$\cfrac{1}{4}\cdot4^2-\cfrac{4}{3}\cdot6+\cfrac{16}{9}|\vec{b}|^2$
$=\cfrac{16}{9}|\vec{b}|^2-4$
$|\overrightarrow{\text{DE}}|=\sqrt{\cfrac{16}{9}|\vec{b}|^2-4}$
また
$\overrightarrow{\text{FM}}=\overrightarrow{\text{OM}}-\overrightarrow{\text{OF}}$ より
$=\cfrac{7}{12}\vec{a}-\cfrac{3}{8}\vec{a}$
$=\cfrac{5}{24}\vec{a}$
$|\overrightarrow{\text{FM}}|=\cfrac{5}{24}\cdot4=\cfrac{5}{6}$
△BDF の面積が $\cfrac{5}{9}$ になることから
$S=\cfrac{1}{2}\cdot\cfrac{5}{6}\sqrt{\cfrac{16}{9}|\vec{b}|^2-4}=\cfrac{5}{9}$
$\sqrt{\cfrac{16}{9}|\vec{b}|^2-4}=\cfrac{4}{3}$
$\cfrac{16}{9}|\vec{b}|^2-4=\cfrac{16}{9}$
$\cfrac{16}{9}|\vec{b}|^2=\cfrac{52}{9}$
$|\vec{b}|^2=\cfrac{13}{4}$
$|\vec{b}|=\cfrac{\sqrt{13}}{2}$ (答え)
SNSでシェア