【空間ベクトル】正四面体の中にできる三角形の面積(神戸大2018理系第1問・文系第1問)

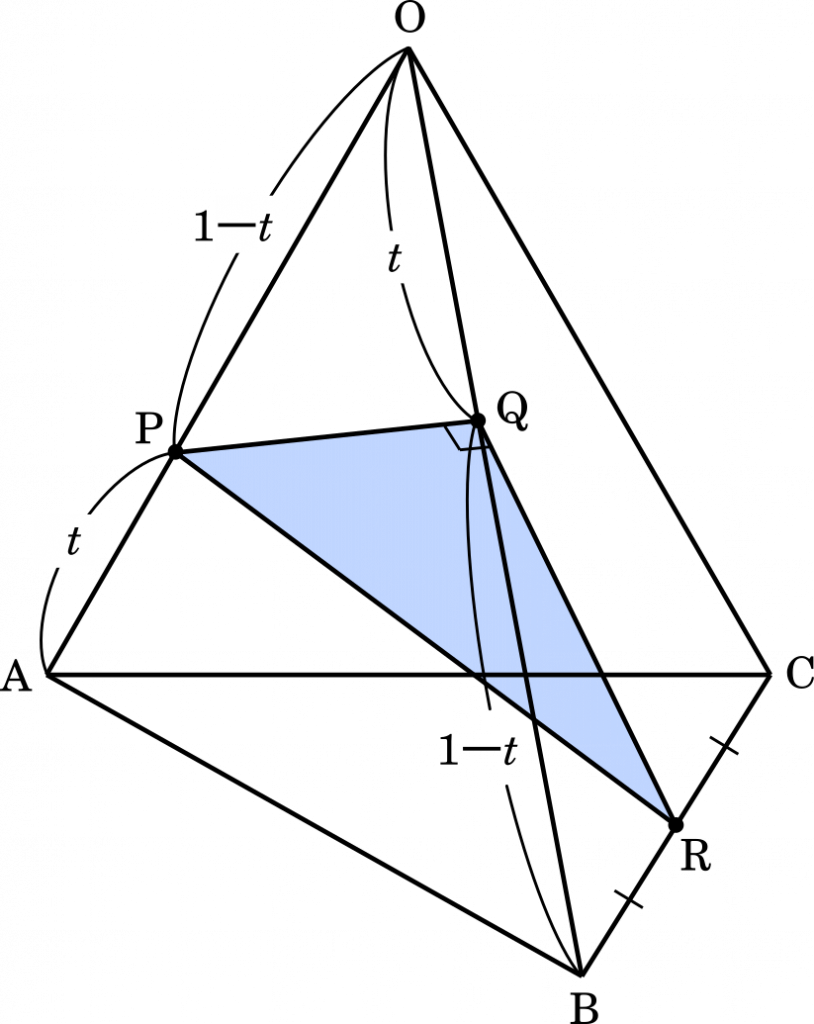
$t$ を $0<t<1$ を満たす実数とする。OABC を 1 辺の長さが 1 の正四面体とする。辺 OA を $1-t:t$ に内分する点を P，辺 OB を $t:1-t$ に内分する天を Q，辺 BC の中点を R とする。また $\vec{a}=\overrightarrow{\text{OA}},\vec{b}=\overrightarrow{\text{OB}},\vec{c}=\overrightarrow{\text{OC}}$ とする。以下の問に答えよ。

(1) $\overrightarrow{\text{QP}}$ と $\overrightarrow{\text{QR}}$ を $t,\vec{a},\vec{b},\vec{c}$ を用いて表わせ。

(2) $\angle\text{PQR}=\cfrac{\pi}{2}$ のとき，$t$ の値を求めよ。

(3) $t$ が (2) で求めた値をとるとき，$\triangle\text{PQR}$ の面積を求めよ。

ベクトルの引き算を利用する

(1)から始めます。

$\overrightarrow{\text{QP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OQ}}$
$=(1-t)\vec{a}-t\vec{b}$

$\overrightarrow{\text{QR}}=\overrightarrow{\text{OR}}-\overrightarrow{\text{OQ}}$
$=\cfrac{1}{2}(\vec{b}+\vec{c})-t\vec{b}$
$=\Big(\cfrac{1}{2}-t\Big)\vec{b}+\cfrac{1}{2}\vec{c}$

内積を利用する

(2)に進みます。$\angle\text{PQR}$ が直角なので内積が 0 になります。とりあえず内積の式を作ってみましょう。

$\overrightarrow{\text{QP}}\cdot\overrightarrow{\text{QR}}=0$
$\{(1-t)\vec{a}-t\vec{b}\}\Big\{\Big(\cfrac{1}{2}-t\Big)\vec{b}+\cfrac{1}{2}\vec{c}\Big\}=0$
$(1-t)\Big(\cfrac{1}{2}-t\Big)\vec{a}\cdot\vec{b}+\cfrac{1}{2}(1-t)\vec{a}\cdot\vec{c}-t\Big(\cfrac{1}{2}-t\Big)|\vec{b}|^2-\cfrac{1}{2}t\vec{b}\cdot\vec{c}=0$

ここで OABC は辺の長さが 1 の正四面体であったことを思い出しましょう。つまり，$\vec{a}\cdot\vec{b}$ や $\vec{a}\cdot\vec{c}$ などの内積はすべて等しく，$1\cdot1\cdot\cos\cfrac{\pi}{3}=\cfrac{1}{2}$ です。

$(1-t)\Big(\cfrac{1}{2}-t\Big)\cdot\cfrac{1}{2}+\cfrac{1}{2}(1-t)\cdot\cfrac{1}{2}-t\Big(\cfrac{1}{2}-t\Big)-\cfrac{1}{2}t\cdot\cfrac{1}{2}=0$

両辺を 4 倍して，分数を解消しておきます。

$(1-t)(1-2t)+1-t-t(2-4t)-t=0$
$1-2t-t+2t^2+1-t-2t+4t^2-t=0$
$6t^2-7t+2=0$
$(2t-1)(3t-2)=0$
$t=\cfrac{1}{2},\cfrac{2}{3}$　（答え）

三角形の面積

(3)に進みます。

△PQR は直角三角形なので，QP と QR の長さが分かれば面積を求めるのは難しくありません。

$|\overrightarrow{\text{QP}}|^2=\{(1-t)\vec{a}-t\vec{b}\}^2$
$=(1-t)^2|\vec{a}|^2-2t(1-t)\vec{a}\cdot\vec{b}+t^2|\vec{b}|^2$
$=(1-t)^2-t(1-t)+t^2$
$=1-2t+t^2-t+t^2+t^2$
$=3t^2-3t+1$
$|\overrightarrow{\text{QR}}|^2=\Big\{\Big(\cfrac{1}{2}-t\Big)\vec{b}+\cfrac{1}{2}\vec{c}\Big\}^2$
$=\Big(\cfrac{1}{2}-t\Big)^2|\vec{b}|^2+\Big(\cfrac{1}{2}-t\Big)\vec{b}\cdot\vec{c}+\cfrac{1}{4}|\vec{c}|^2$
$=\cfrac{1}{4}-t+t^2+\cfrac{1}{4}-\cfrac{t}{2}+\cfrac{1}{4}$
$=t^2-\cfrac{3}{2}t+\cfrac{3}{4}$

△PQR の面積は

$S^2=\Big(\cfrac{1}{2}|\overrightarrow{\text{QP}}||\overrightarrow{\text{QR}}|\Big)^2$
$=\cfrac{1}{4}|\overrightarrow{\text{QP}}|^2|\overrightarrow{\text{QR}}|^2$
$=\cfrac{1}{4}(3t^2-3t+1)\Big(t^2-\cfrac{3}{2}t+\cfrac{3}{4}\Big)$

$t=\cfrac{1}{2}$ のとき

$S^2=\cfrac{1}{4}\Big(\cfrac{3}{4}-\cfrac{3}{2}+1\Big)\Big(\cfrac{1}{4}-\cfrac{3}{4}+\cfrac{3}{4}\Big)$
$=\cfrac{1}{4}\cdot\cfrac{1}{4}\cdot\cfrac{1}{4}=\cfrac{1}{64}$

$S=\cfrac{1}{8}$　（答え）

$t=\cfrac{2}{3}$ のとき

$S^2=\cfrac{1}{4}\Big(\cfrac{4}{3}-2+1\Big)\Big(\cfrac{4}{9}-1+\cfrac{3}{4}\Big)$
$=\cfrac{1}{4}\cdot\cfrac{1}{3}\cdot\cfrac{7}{36}$
$=\cfrac{7}{432}$

$S=\cfrac{\sqrt{7}}{12\sqrt{3}}=\cfrac{\sqrt{21}}{36}$　（答え）