【数III】積分すると同じ形になる 式をまるごと文字に置きかえ
以下の不定積分を求めよ。
$\displaystyle\int\frac{1}{x(\log x)^2}\space dx$

分数のヤツ苦手。

分数というよりかけ算になってることに気づくべき。だから部分積分やるの。
部分積分
部分積分法
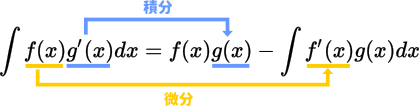
かけ算の積分が出てきたら部分積分です。考え方としてはいったん微分する側と積分する側を決めて公式に当てはめていきます。一般的には微分したときに $x$ が消える方を微分側に決めます。
この式をかけ算になおすと
$\displaystyle\int\frac{1}{x}\cdot\frac{1}{(\log x)^2}\space dx$

微分側決めようとしたけど、微分してもどっちも $x$ 消えませんよ。

そうそう。だから今回は積分側から決めるしかないかな。$\displaystyle \frac{1}{x}$ って積分したら $\log x$ になるでしょ?これでやってみるしかなさそうね。
$\displaystyle\int(\log x)’\cdot\frac{1}{(\log x)^2}\space dx$
$\displaystyle =\log x\cdot\frac{1}{(\log x)^2}+C-\int\log x\cdot\left\{\frac{1}{(\log x)^2}\right\}’\space dx$($C$は積分定数)
分数の微分公式にこの形がありました。
商の導関数 $\displaystyle \left\{\frac{1}{g(x)}\right\}’=-\frac{g'(x)}{\{g(x)\}^2}$
公式に当てはめると
$\displaystyle =\frac{1}{\log x}+C-\int\log x\cdot\left\{-\frac{\frac{2}{x}\log x}{(\log x)^4}\right\}\space dx$

$(\log x)^2$ は合成関数だから、微分して $\displaystyle 2(\log x)\cdot\frac{1}{x}$ になる。$\log x$ を微分した $\displaystyle \frac{1}{x}$ をかけるのを忘れないように。
式を整理すると
$\displaystyle =\frac{1}{\log x}+C+2\int\frac{1}{x(\log x)^2}\space dx$

これ解けないですよ。

このままだと解けないね。でも、式の一部が $\displaystyle \int\frac{1}{x(\log x)^2}\space dx$ ってなってて、これってもとの式と同じだよね?

ですね。

で、こういうパターンがきたら文字に置きかえるの。もう一回最初からいくよ。
$I=\displaystyle\int\frac{1}{x(\log x)^2}\space dx$ として
$\displaystyle I=\frac{1}{\log x}+C+2\int\frac{1}{x(\log x)^2}\space dx$
$\displaystyle I=\frac{1}{\log x}+C+2I$
$I$ を移項して
$\displaystyle -I=\frac{1}{\log x}+C$
$\displaystyle I=-\frac{1}{\log x}+C$(答え)

最後 $-C$ じゃないんですか?

$C$ は積分定数だから符号は意味なくて常にプラスでオッケーって思っておいて。
今回のポイントは
積分したらもとの式と同じ部分ができる → もとの式をまるごと文字におきかえ
解法パターンの一つとしてマスターしましょう。
SNSでシェア