接線とx軸との交点からつくられる数列(神戸大2018文系第2問)
$f(x)=(2x-1)^3$ とする。数列 $\{x_n\}$ を次のように定める。
$x_1=2$ であり,$x_{n+1}$ $(n\geqq1)$ は点 $(x_n,f(x_n))$ における曲線 $y=f(x)$ の接線と $x$ 軸の交点の $x$ 座標とする。
以下の問に答えよ。
(1) 点 $(t,f(t))$ における曲線 $y=f(x)$ の接線の方程式を求めよ。また $t\not=\cfrac{1}{2}$ のときに,その接線と $x$ 軸の交点の $x$ 座標を求めよ。
(2) $x_n>\cfrac{1}{2}$ を示せ。また $x_n$ を $n$ の式で表せ。
(3) $|x_{n+1}-x_n|<\cfrac{3}{4}\times10^{-5}$ を満たす最小の $n$ を求めよ。ただし $0.301<\log_{10}2<0.302$,$0.477<\log_{10}3<0.478$ は用いてよい。
接線の方程式と x 軸との交点
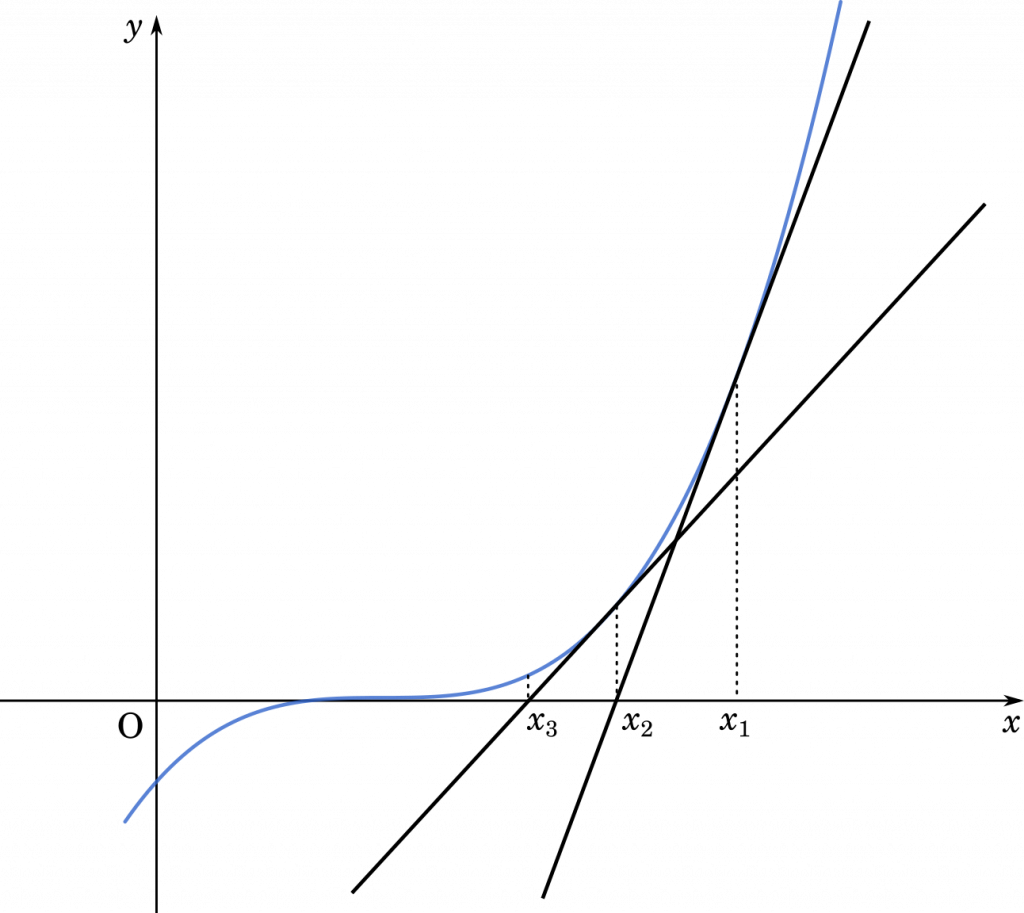
(1)から始めます。
まずは微分して接線の傾きを求めましょう。
$f(x)=(2x-1)^3$
$=8x^3-12x^2+6x+1$
$f'(x)=24x^2-24x+6$
$=6(4x^2-4x+1)$
$=6(2x-1)^2$
$x=t$ のときの接線の傾きは $6(2t-1)^2$ となります。よって,$(t,f(t))$ を通る接線の方程式は
$y=6(2t-1)^2(x-t)+(2t-1)^3$
$=(2t-1)^2(\{6(x-t)+2t-1\}$
$=(2t-1)^2(6x-4t-1)$ (答え)
次に $x$ 軸との交点を求めます。
$(2t-1)^2(6x-4t-1)=0$ とすると
$2t-1$ は $t=\cfrac{1}{2}$ のとき $0$ となりますが,問題文より $t\not=\cfrac{1}{2}$ だから,$2t-1\not=0$ となります。
$6x-4t-1=0$
$x=\cfrac{4t+1}{6}$ (答え)
数学的帰納法
(2)に進みます。


(1)より,$t=x_1$ とすると
$x_2=\cfrac{4x_1+1}{6}$
$=\cfrac{2}{3}x_1+\cfrac{1}{6}$
となります。ここから漸化式は
$x_{n+1}=\cfrac{2}{3}x_n+\cfrac{1}{6}$ $(n=1,2,3,\cdots)$
これをもとに不等式を証明しましょう。
すべての自然数 $n$ において,$x_n>\cfrac{1}{2}$ が成り立つことを数学的帰納法を用いて示す。
[I] $n=1$ のとき
$x_1=2>\cfrac{1}{2}$
[II] $n=k$ のとき $x_k>\cfrac{1}{2}$ が成り立つと仮定すると
$\cfrac{2}{3}x_k>\cfrac{1}{3}$
$\cfrac{2}{3}x_k+\cfrac{1}{6}>\cfrac{1}{2}$
$x_{k+1}>\cfrac{1}{2}$
[I],[II] より,すべての自然数 $n$ に対し,$x_n>\cfrac{1}{2}$ が成り立つ。(証明終わり)
次に数列の一般項を求めます。

$\alpha=\cfrac{2}{3}\alpha+\cfrac{1}{6}$ とすると
$\cfrac{1}{3}\alpha=\cfrac{1}{6}$
$\alpha=\cfrac{1}{2}$
となるので
$\begin{matrix}&x_{n+1}&=&\cfrac{2}{3}x_n+\cfrac{1}{6}\\-)&\alpha&=&\cfrac{2}{3}\alpha+\cfrac{1}{6}\\\hline&x_{n+1}-\alpha&=&\cfrac{2}{3}(x_n-\alpha)\end{matrix}$
$x_{n+1}-\cfrac{1}{2}=\cfrac{2}{3}\Big(x_n-\cfrac{1}{2}\Big)$ ・・・①
ここで,$x_n-\cfrac{1}{2}=b_n$ とすると
$b_1=x_1-\cfrac{1}{2}$
$=2-\cfrac{1}{2}=\cfrac{3}{2}$
となるので,①は
$b_{n+1}=\cfrac{2}{3}b_n$
よって,$b_n$ は初項 $\cfrac{3}{2}$,公比 $\cfrac{2}{3}$ の等比数列だから,一般項は
$b_n=\cfrac{3}{2}\Big(\cfrac{2}{3}\Big)^{n-1}$
したがって
$x_n-\cfrac{1}{2}=\cfrac{3}{2}\Big(\cfrac{2}{3}\Big)^{n-1}$
$x_n=\cfrac{1}{2}+\cfrac{3}{2}\Big(\cfrac{2}{3}\Big)^{n-1}$ (答え)
対数を用いる
(3)に進みます。
まずは,$x_{n+1}-x_n$ を計算しましょう。
$x_{n+1}-x_n$
$=\cfrac{1}{2}+\cfrac{3}{2}\Big(\cfrac{2}{3}\Big)^{n}-\cfrac{1}{2}-\cfrac{3}{2}\Big(\cfrac{2}{3}\Big)^{n-1}$
$=\cfrac{3}{2}\Big\{\Big(\cfrac{2}{3}\Big)^n-\Big(\cfrac{2}{3}\Big)^{n-1}\Big\}$
$=\cfrac{3}{2}\Big(\cfrac{2}{3}\Big)^n\Big\{1-\Big(\cfrac{2}{3}\Big)^{-1}\Big\}$
$=\cfrac{3}{2}\Big(\cfrac{2}{3}\Big)^n\Big(1-\cfrac{3}{2}\Big)$
$=\cfrac{3}{2}\Big(\cfrac{2}{3}\Big)^n\Big(-\cfrac{1}{2}\Big)$
$=-\cfrac{3}{4}\Big(\cfrac{2}{3}\Big)^n$
よって
$|x_{n+1}-x_n|=\cfrac{3}{4}\Big(\cfrac{2}{3}\Big)^n$
となるので
$\cfrac{3}{4}\Big(\cfrac{2}{3}\Big)^n<\cfrac{3}{4}\times10^{-5}$
とすると
$\Big(\cfrac{2}{3}\Big)^n<10^{-5}$
両辺の対数をとります。
$\log_{10}\Big(\cfrac{2}{3}\Big)^n<\log_{10}10^{-5}$
$n\log_{10}\cfrac{2}{3}<-5\log_{10}10$
$n(\log_{10}2-\log_{10}3)<-5$
$n(\log_{10}3-\log_{10}2)>5$
$n>\cfrac{5}{\log_{10}3-\log_{10}2}$
ここで,$0.301<\log_{10}2<0.302$,$0.477<\log_{10}3<0.478$ を使って $\log_{10}3-\log_{10}2$ の範囲を考えます。

範囲は,引き算をしたときに差が最も小さくなるときと大きくなるときで考えます。
差がもっとも小さくなるのは,$0.477-0.302$ のときで,差がもっとも大きくなるのは $0.478-0.301$ のときです。
よって
$0.477-0.302<\log_{10}3-\log_{10}2<0.478-0.301$
$0.175<\log_{10}3-\log_{10}2<0.177$


$0.175<\log_{10}3-\log_{10}2$
$\cfrac{1}{0.175}>\cfrac{1}{\log_{10}3-\log_{10}2}$
$\cfrac{5}{0.175}>\cfrac{5}{\log_{10}3-\log_{10}2}$
$28.57\cdots>\cfrac{5}{\log_{10}3-\log_{10}2}$
また
$\log_{10}3-\log_{10}2<0.177$
$\cfrac{5}{\log_{10}3-\log_{10}2}>\cfrac{5}{0.177}$
$\cfrac{5}{\log_{10}3-\log_{10}2}>28.24\cdots$
よって
$n>28.57\cdots$
したがって,不等式を満たす最小の $n$ は 29。(答え)
SNSでシェア