絶対値のある関数と直線の関係(神戸大2016理系第2問)

$a$ を正の定数とし，$f(x)=|x^2+2ax+a|$ とおく。以下の問に答えよ。

(1) $y=f(x)$ のグラフの概形をかけ。

(2) $a=2$ とする。すべての実数 $x$ に対して $f(x)\geqq2x+b$ が成り立つような実数 $b$ の取りうる値の範囲を求めよ。

(3) $0<a\leqq\cfrac{3}{2}$ とする。すべての実数 $x$ に対して $f(x)\geqq2x+b$ が成り立つような実数 $b$ の取りうる値の範囲を $a$ を用いて表わせ。また，その条件をみたす点 $(a,b)$ の領域を $ab$ 平面上に図示せよ。

正のときと負のときに分けて考える

(1)から始めます。

絶対値があるので，中身が正の数になるときと負の数になるときで分けて考えます。

グラフを考えるために，いったん平方完成して頂点を求めておきましょう。

$x^2+2ax+a$
$=(x+a)^2-a^2+a$

また $x^2+2ax+a=0$ とすると

$x=-a\pm\sqrt{a^2-a}$

$y=x^2+2ax+a$ のグラフを描いて，$x$ 軸の下側にくる部分を反転させると絶対値のグラフになります。ただし，頂点の $y$ 座標が $x$ 軸より上にくる場合は，反転させる部分がないのでそのまま 2 次関数の曲線を描くことになります。

頂点の $y$ 座標が $x$ 軸より上にくるとき

$-a^2+a>0$
$a^2-a<0$
$a(a-1)<0$
よって $0<a<1$

したがって，グラフの概形は

・$a\geqq1$ のとき

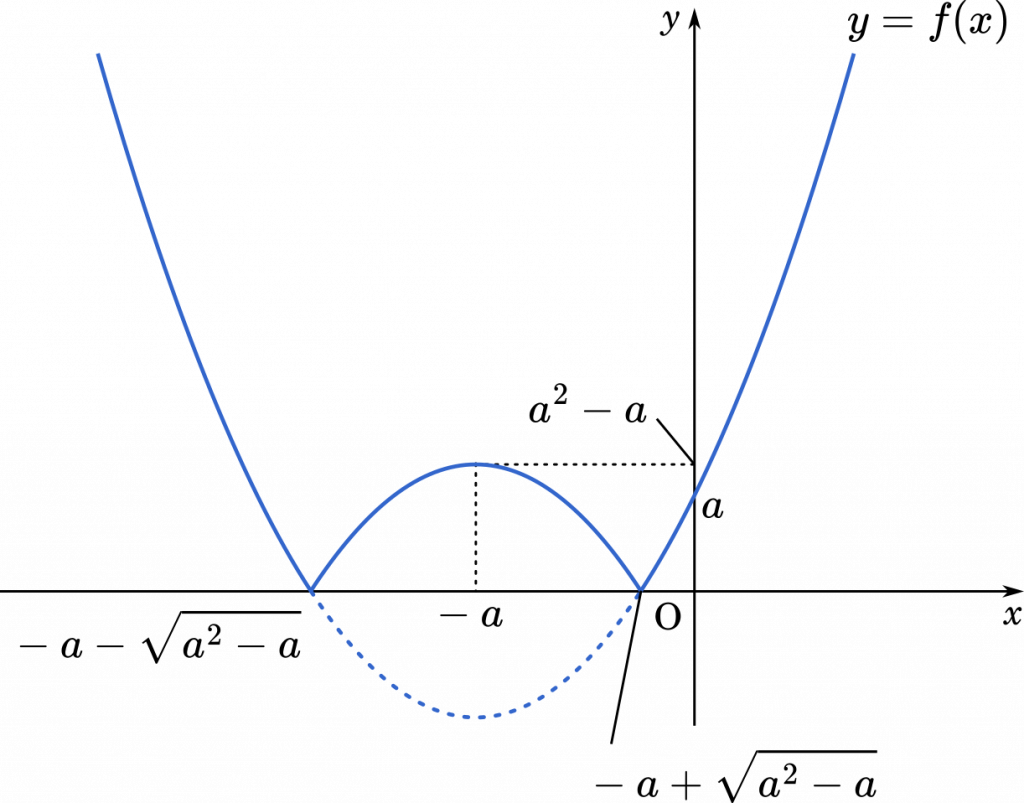
・$0<a<1$ のとき

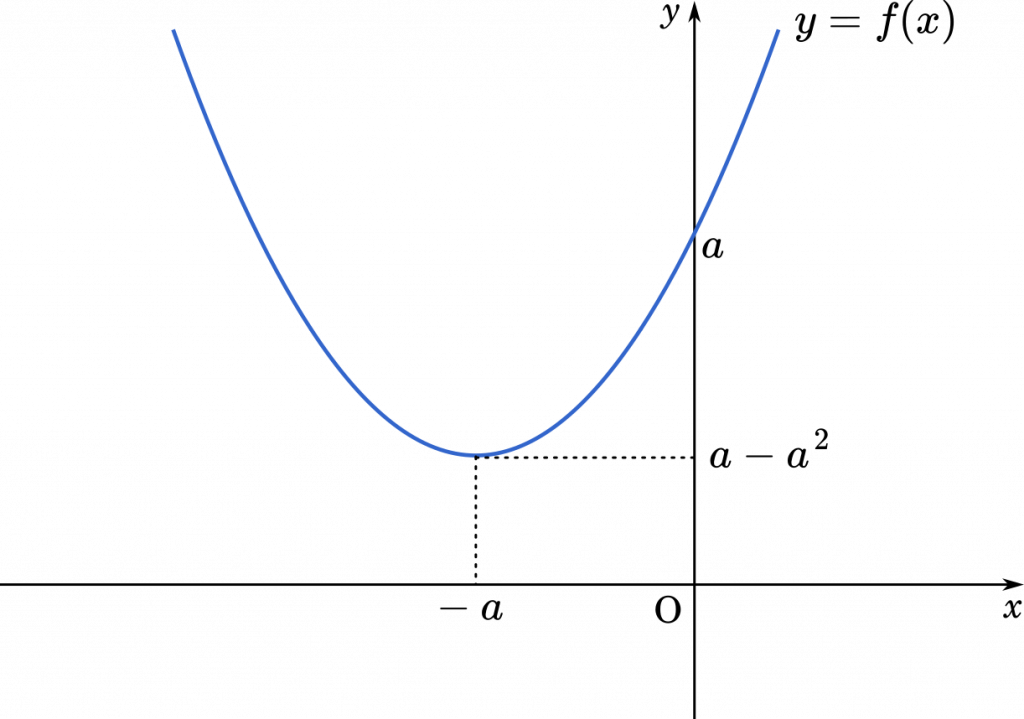
関数と直線の関係

(2)に進みます。

$a=2$ とすると

$f(x)=|x^2+4x+2|$

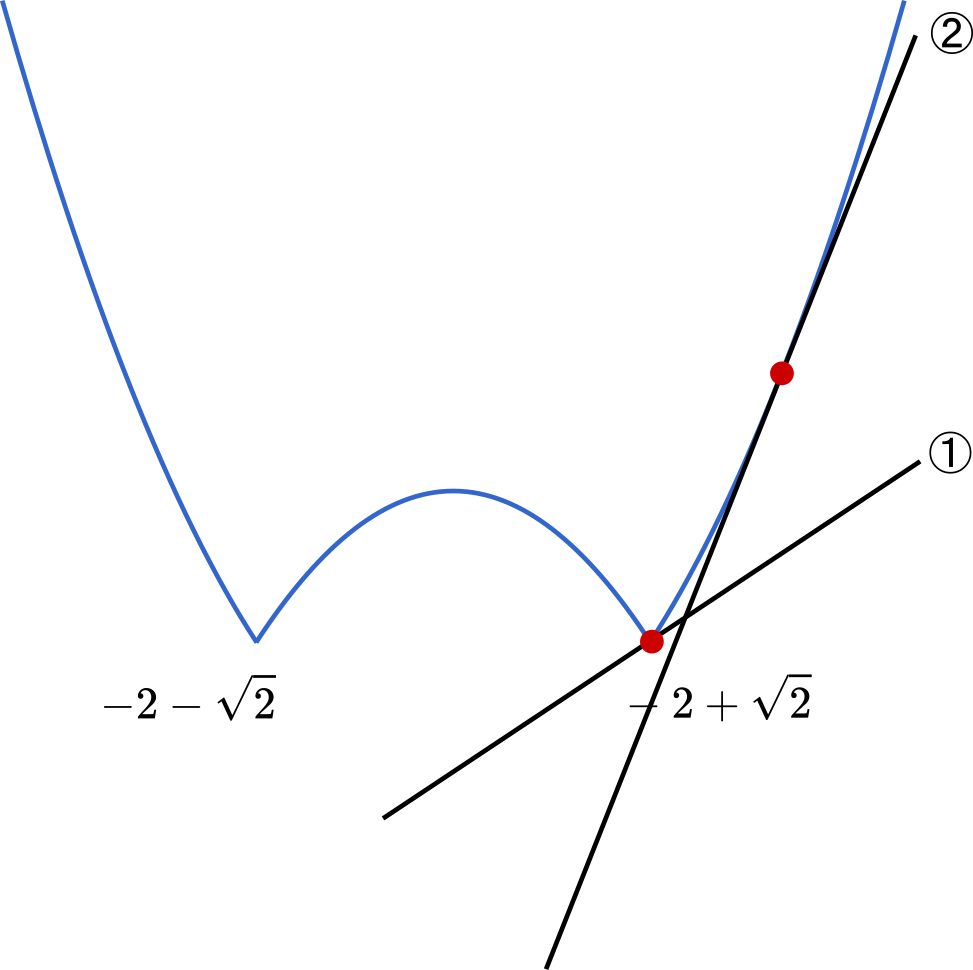
$f(x)\geqq2x+b$ ということは，曲線と直線をタテ方向で比べたとき，曲線が直線よりも上にあるということです。

$y=2x+b$ は $b$ の値によってタテ方向に平行移動するので，いろいろパターンを考えてみると，①と②の場合が考えられます。グラフはあくまで概形なので，この段階ではどちらになるかは分かりません。

②の場合について考えてみましょう。このとき，直線は曲線の接線になるので，傾きは 2 です。

$y=x^2+4x+2$ として

$y’=2x+4$

$2x+4=2$　とすると
$2x=-2$
$x=-1$

曲線と $x$ 軸の交点は

$x=-2\pm\sqrt{2^2-2}=-2\pm\sqrt{2}$

だから

$-1<-2+\sqrt{2}$

より，②の形にはなりません。

したがって，①の形で考えると，直線は $(-2+\sqrt{2},0)$ を通るので

$y\geqq ax+b$
$0\geqq2(-2+\sqrt{2})+b$
$b\leqq4-2\sqrt{2}$　（答え）

さらに関数と直線の関係

(3)に進みます。

(2)と同様に，曲線と直線がどこで接するかを考えていきましょう。

(i) $0<a<1$ のとき

(1)で求めたように，この場合のグラフは曲線全体が $x$ 軸より上にあります。

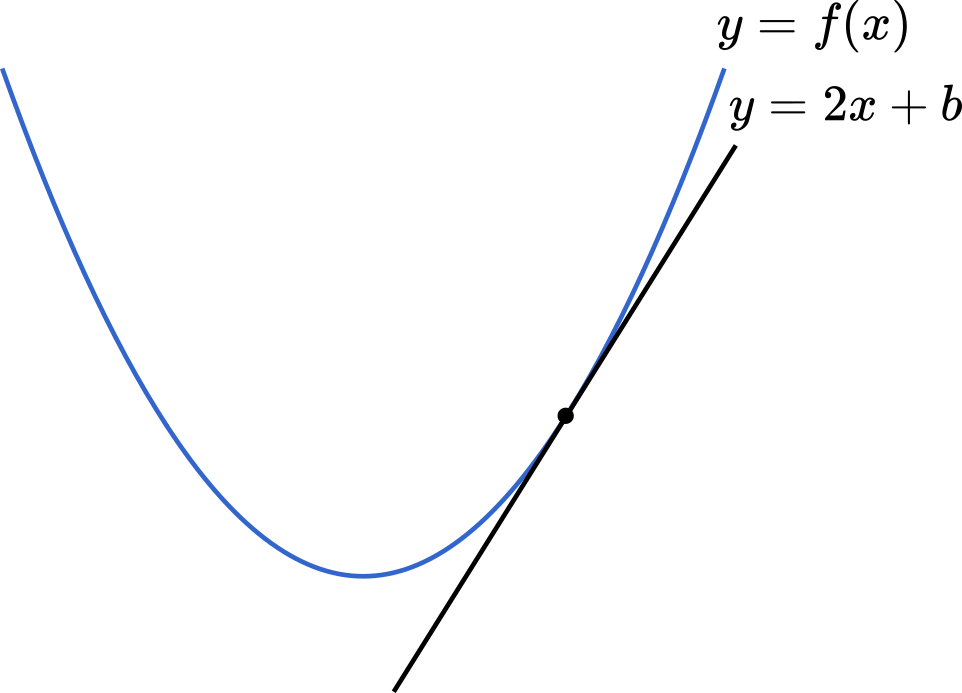
傾き 2 として，曲線に接する直線を求めてみましょう。

$f(x)=x^2+2ax+a$ より

$f'(x)=2x+2a$

傾きが 2 だから

$2x+2a=2$
$x+a=1$
$x=1-a$

傾きが 2 で $(1-a,(1-a)^2+2a(1-a)+a)$ を通る直線の式は

$y=2(x-1+a)+(1-a)^2+2a(1-a)+a$
$=2x-2+2a+1-2a+a^2+2a-2a^2+a$
$=2x-a^2+3a-1$

これと $y=2x+b$ を比べると

$b=-a^2+3a-1$

よって，すべての実数 $x$ に対して $f(x)\geqq2x+b$ が成り立つような実数 $b$ の取りうる値の範囲は

$b\leqq-a^2+3a-1$

(ii) $1\leqq a\leqq\cfrac{3}{2}$ のとき

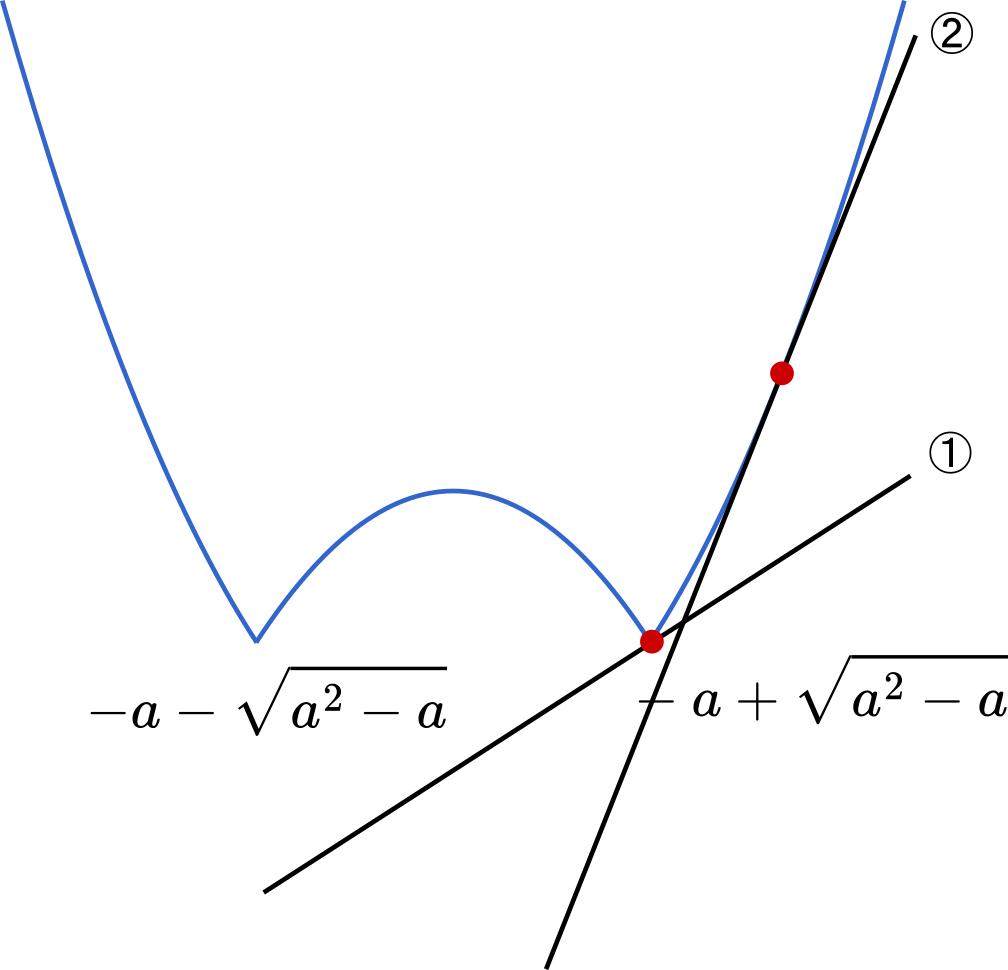
ここは，(2)のときと同じように 2 つの可能性を考える必要があります。

直線の式を，$y=2x-a^2+3a-1$ とすると

$x=-a+\sqrt{a^2-a}$ のとき

$y=2(-a+\sqrt{a^2-a})-a^2+3a-1$

$=-2a+2\sqrt{a^2-a}-a^2+3a-1$
$=2\sqrt{a^2-a}-a^2+a-1$

そこで，$1\leqq a\leqq\cfrac{3}{2}$ の範囲で，この式の値がどう変化するかを増減表を作って調べて見ましょう。

$g(a)=2\sqrt{a^2-a}-a^2+a-1$　とすると

$g(a)=2(a^2-a)^{\small{\frac{1}{2}}}-a^2+a-1$
$g'(a)=(a^2-a)^{\small{-\frac{1}{2}}}(2a-1)-2a+1$

$=\cfrac{2a-1}{\sqrt{a^2-a}}-2a+1$

$\cfrac{2a-1}{\sqrt{a^2-a}}-2a+1=0$ とすると

$\cfrac{2a-1}{\sqrt{a^2-a}}=2a-1$
$\cfrac{1}{\sqrt{a^2-a}}=1$
$\sqrt{a^2-a}=1$
$a^2-a=1$
$a^2-a-1=0$
$a=\cfrac{1\pm\sqrt{5}}{2}$

$a>0$ より

$a=\cfrac{1+\sqrt{5}}{2}$

この値のおおよその大きさを考えましょう。

$\sqrt{4}<\sqrt{5}<\sqrt{9}$ より

$2<\sqrt{5}<3$
$3<1+\sqrt{5}<4$
$\cfrac{3}{2}<\cfrac{1+\sqrt{5}}{2}<2$

つまり，$g(a)$ は $1\leqq a\leqq\cfrac{3}{2}$ の範囲で極値をとりません。

また，たとえば $a=1$ のとき $g(a)$ は負の値をとるので，増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|}\hline a&1&\cdots&\frac{3}{2}\\\hline g'(a)&-&-&-\\\hline g(a)&-1&\searrow\\\hline\end{array}$

$g(1)=2\sqrt{1^2-1}-1^2+1-1=-1$

$1\leqq a\leqq\cfrac{3}{2}$ の範囲で $g(a)$ は単調減少である。よって

$g(a)<0$

つまり上のグラフで言えば①ではなく②の方が正解ということです。

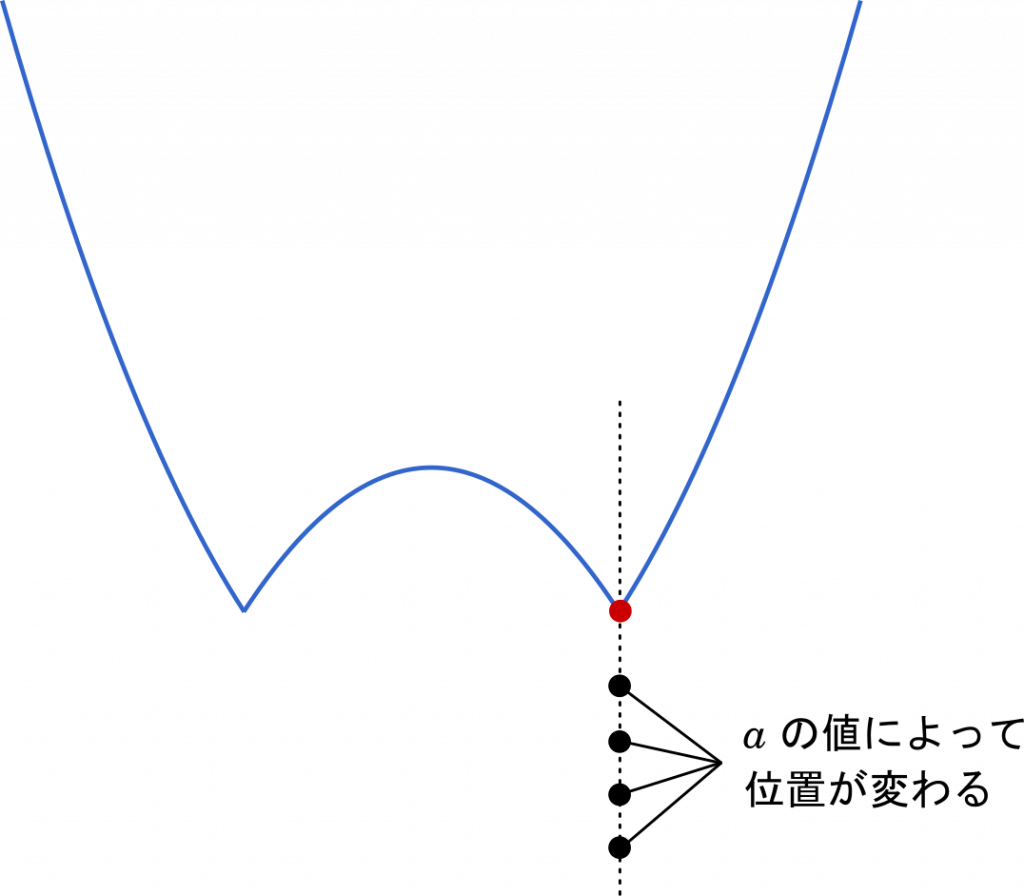
図やっていることはこういうことです。$x$ の値を $-a+\sqrt{a^2-a}$ に固定して $a$ の値を変化させると，タテ方向に点が移動することになります。このとき，$a$ の値によって $y$ 座標が 0 になるかどうかを調べてみたら，$1\leqq a\leqq\cfrac{3}{2}$ の範囲で $y$ 座標はつねに負の数で 0 になることはない，ということです。

(i)，(ii)より

$b\leqq-a^2+3a-1$

最後にこの不等式の表す領域をグラフにしましょう。

$b=-a^2+3a-1$ として，平方完成すると

$=-(a^2-3a)-1$
$=-\Big(a-\cfrac{3}{2}\Big)^2+\cfrac{9}{4}-1$
$=-\Big(a-\cfrac{3}{2}\Big)^2+\cfrac{5}{4}$

したがって

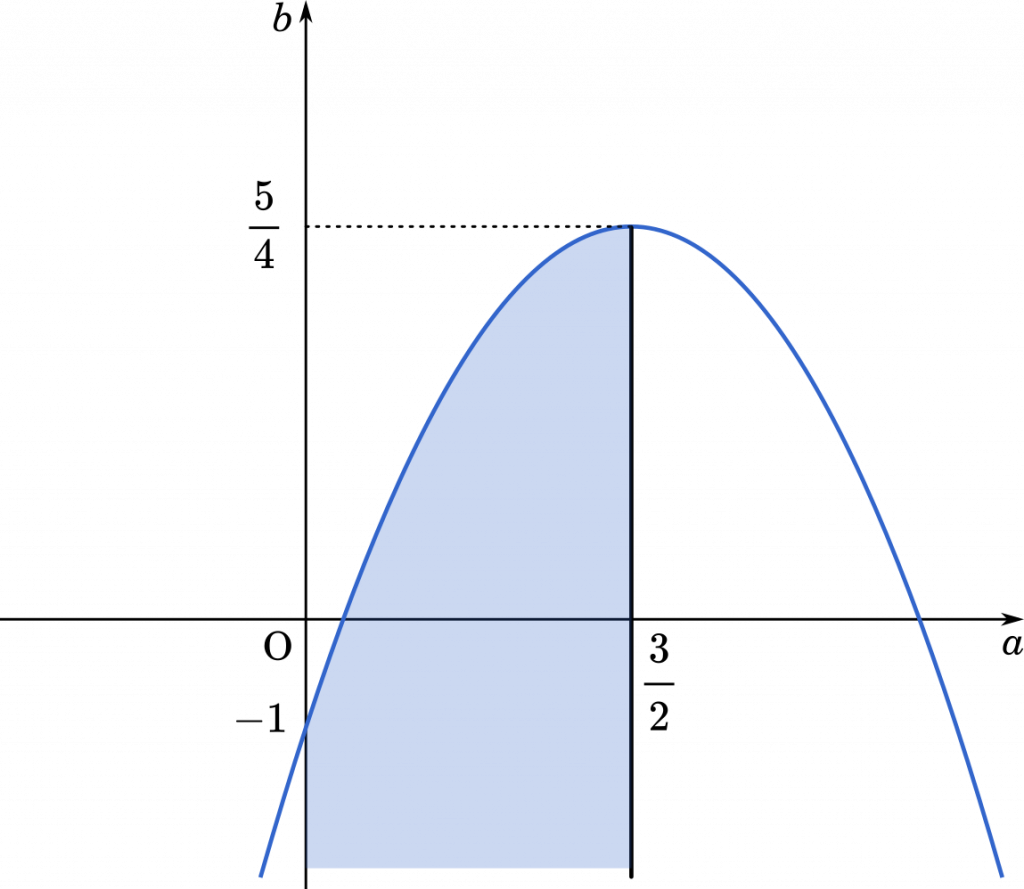
領域は軸 $a=\cfrac{3}{2}$ を含み，軸 $a=0$ を含まない。
（答え）