【スマホで読む・わかりやすい】センター数学IA2015追試【解説・正解・問題】

第6問　解答・解説

ア 5　イ 7　ウ エ オ 2 6 3

カ 4　キ クケ コ 2 42 3

サ シ ス 2 6 3

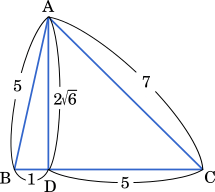
三平方の定理より

AB = $\sqrt{1^2+(2\sqrt{6})^2}$

$=\sqrt{1+24}=\sqrt{25}=5$

・・・ア

AC = $\sqrt{5^2+(2\sqrt{6})^2}$

$=\sqrt{25+24}=\sqrt{49}=7$

・・・イ

次に，△ABC の内接円の半径は，△ABC の面積を求めた上で，公式 $S=\cfrac{1}{2}r(a+b+c)$ を用いて求めるとよい。

$S=\cfrac{1}{2}\cdot6\cdot2\sqrt{6}=6\sqrt{6}$

$S=\cfrac{1}{2}r(a+b+c)$ より

$6\sqrt{6}=\cfrac{1}{2}r(5+6+7)$

$6\sqrt{6}=9r$

$r=\cfrac{2\sqrt{6}}{3}$

・・・ウエオ

内接円と辺 AB が接する点を G として，それぞれの辺の比を求める。CE = $x$ とおくと

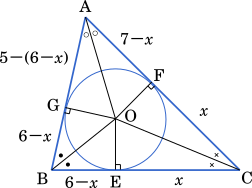
$5-(6-x)=7-x$

$x-1=7-x$

$2x=8$

$x=4$

よって

CE = CF = $4$

・・・カ

CO を求めると，三平方の定理より

CO = $\sqrt{4^2+\bigg(\cfrac{2\sqrt{6}}{3}\bigg)^2}$

$=\sqrt{16+\cfrac{24}{9}}$

$=\sqrt{16+\cfrac{8}{3}}$

$=\sqrt{\cfrac{56}{3}}$

$=\cfrac{2\sqrt{14}}{\sqrt{3}}$

$=\cfrac{2\sqrt{42}}{3}$

・・・キクケコ

内接円 I と辺 CE の接する点を P，辺 EF と接する点を Q とおく。

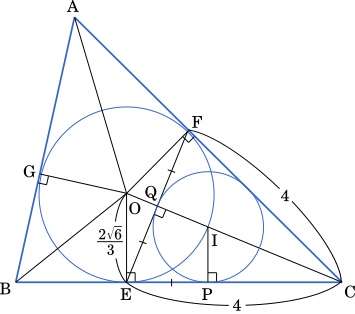
CE = CF より △CEF は二等辺三角形である。よって，CQ = EQ が成り立つ。

ここで，EF の長さを求める。△ACB において余弦定理より

$5^2=6^2+7^2-2\cdot6\cdot7\cos\angle\text{ACB}$

$25=36+49-84\cos\angle\text{ACB}$

$84\cos\angle\text{ACB}=60$

$\cos\angle\text{ACB}=\cfrac{5}{7}$

△CEF において余弦定理より

$\text{EF}^2=4^2+4^2-2\cdot4\cdot4\cdot\cfrac{5}{7}$

$=\cfrac{64}{7}$

$\text{EF}=\cfrac{8\sqrt{7}}{7}$

よって，EQ = $\cfrac{4\sqrt{7}}{7}$

また，EQ = EP だから，EP = $\cfrac{4\sqrt{7}}{7}$

△CIP ∽ △COE より

CI : CO = CP : CE

CI : $\cfrac{2\sqrt{42}}{3}=4-\cfrac{4\sqrt{7}}{7}:4$

$=\cfrac{7-\sqrt{7}}{7}:1$

CI = $\cfrac{2\sqrt{42}}{3}\cdot\cfrac{7-\sqrt{7}}{7}$

$=\cfrac{14\sqrt{42}-14\sqrt{6}}{21}$

$=\cfrac{2\sqrt{42}-2\sqrt{6}}{3}$

IO = CP $-$ CI だから

IO = $\cfrac{2\sqrt{42}}{3}-\cfrac{2\sqrt{42}-2\sqrt{6}}{3}$

$=\cfrac{2\sqrt{6}}{3}$

・・・サシス

第６問　問題文

長さ $6$ の線分 BC を $1:5$ に内分する点 D をとり，D を通り BC に直交する直線上に点 A を AD $=2\sqrt{6}$ となるようにとる。

このとき，AB=$\boxed{\text{ ア }}$，AC=$\boxed{\text{ イ }}$ であるから，△ABC の内接円の半径は $\displaystyle \frac{\boxed{\text{ ウ }}\sqrt{\boxed{\text{ エ }}}}{\boxed{\text{ オ }}}$ である。

内接円が辺 BC，AC に接する点を E，F とすると，CE=CF=$\boxed{\text{ カ }}$ であるから，内心 O と頂点 C との距離は

CO=$\displaystyle \frac{\boxed{\text{ キ }}\sqrt{\boxed{\text{ クケ }}}}{\boxed{\text{ コ }}}$

である。

△CEF の内心と △ABC の内心の間の距離は

$\displaystyle \frac{\boxed{\text{ サ }}\sqrt{\boxed{\text{ シ }}}}{\boxed{\text{ ス }}}$

である。