【スマホで読む・わかりやすい】センター数学IIB2016本試【解説・正解・問題】

第2問　解答・解説

ア イ 4 2　ウ エ 4 4　オ カキ 7 12

クケ コ －1 2　サシ スセ 25 48

ソ 1　タ 2　チ 2　ツ 1　テ 6　ト 2

ナ ニ ヌ 6 4 4

ネノ ハ ヒ －1 3 2

(1)

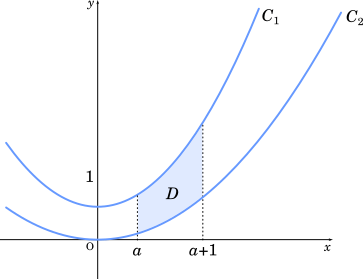
$\displaystyle S=\int_{\small{a}}^{\small{a+1}}\cfrac{1}{2}x^2+\cfrac{1}{2}-\cfrac{1}{4}x^2dx$

$\displaystyle=\int_{\small{a}}^{\small{a+1}}\cfrac{1}{4}x^2+\cfrac{1}{2}dx$

・・・アイ

$=\Big[\cfrac{x^3}{12}+\cfrac{x}{2}\Big]_{\small{a}}^{\small{a+1}}$

$=\Big\{\cfrac{(a+1)^3}{12}+\cfrac{a+1}{2}\Big\}-\Big(\cfrac{a^3}{12}+\cfrac{a}{2}\Big)$

$=\cfrac{3a^2}{12}+\cfrac{3a}{12}+\cfrac{1}{12}+\cfrac{1}{2}$

$=\cfrac{a^2}{4}+\cfrac{a}{4}+\cfrac{7}{12}$

・・・ウエオカキ

式を $\cfrac{1}{4}(a^2+a)+\cfrac{7}{12}$
と変形して平方完成すると

$=\cfrac{1}{4}\Big(a+\cfrac{1}{2}\Big)^2-\cfrac{1}{16}+\cfrac{7}{12}$

$=\cfrac{1}{4}\Big(a+\cfrac{1}{2}\Big)^2+\cfrac{25}{48}$

したがって，$S$ は $a=\cfrac{-1}{2}$ で最小値 $\cfrac{25}{48}$ をとる。

・・・クケコサシスセ

(2)

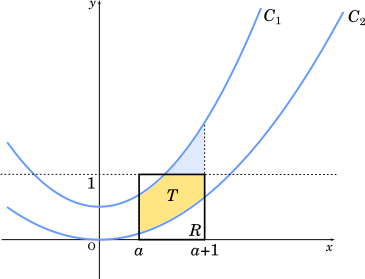
直線 $y=1$ と $C_1$ の交点を求めると

$1=\cfrac{1}{2}x^2+\cfrac{1}{2}$

$\cfrac{1}{2}x^2=\cfrac{1}{2}$

$x^2=1$

$x=\pm1$

したがって，$(\pm1,1)$

・・・ソ

$C_2$ との交点を求めると

$1=\cfrac{1}{4}x^2$

$x^2=4$

$x=\pm2$

したがって，$(\pm2,1)$

・・・タ

次に，正方形 $R$ と図形 $D$ の共通部分が空集合になる場合を考えると，以下の図のようになる。

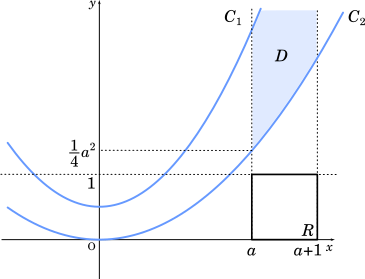
よって，$T$ が空集合にならないのは

$\cfrac{1}{4}a^2\leqq1$

式を変形して

$a^2\leqq4$

$a^2-4\leqq0$

$(a+2)(a-2)\leqq0$

$-2\leqq a \leqq 2$

$a\gt0$ より

$0\leqq a\leqq 2$

・・・チ

また，$1\leqq a\leqq 2$ の範囲で $a$ が増加するとき，$T$ は減少する。

・・・ツ

したがって，$T$ が最大になるのは，$0\leqq a\leqq1$ のときである。

面積 $U$ を求めると

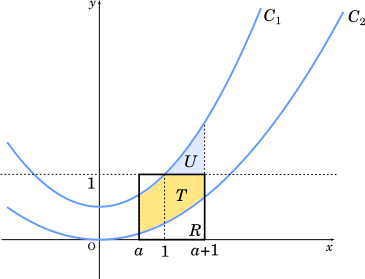
$\displaystyle U=\int_{\small{1}}^{\small{a+1}}\cfrac{1}{2}x^2+\cfrac{1}{2}-1\space dx$

$\displaystyle =\int_{\small{1}}^{\small{a+1}}\cfrac{1}{2}x^2-\cfrac{1}{2}\space dx$

$=\Big[\cfrac{x^3}{6}-\cfrac{x}{2}\Big]_{\small{1}}^{\small{a+1}}$

$=\Big\{\cfrac{(a+1)^3}{6}-\cfrac{a+1}{2}\Big\}-\Big(\cfrac{1}{6}-\cfrac{1}{2}\Big)$

$=\cfrac{a^3+3a^2+3a}{6}-\cfrac{a}{2}$

$=\cfrac{a^3}{6}+\cfrac{a^2}{2}$

・・・テト

よって，面積 $T$ は $D$ から $U$ を引いたものだから

$T=\cfrac{a^2}{4}+\cfrac{a}{4}+\cfrac{7}{12}-\cfrac{a^3}{6}-\cfrac{a^2}{2}$

$=-\cfrac{a^3}{6}-\cfrac{a^2}{4}+\cfrac{a}{4}+\cfrac{7}{12}\cdots\cdots$①

・・・ナニヌ

$T$ の増減を調べると, $T$ を $a$ で微分して

$T’=-\cfrac{a^2}{2}-\cfrac{a}{2}+\cfrac{1}{4}$

$-\cfrac{a^2}{2}-\cfrac{a}{2}+\cfrac{1}{4}=0$ とおくと

$2a^2+2a-1=0$

$a=\cfrac{-1\pm\sqrt{1+2}}{2}=\cfrac{-1\pm\sqrt{3}}{2}$

$\def\arraystretch{1.25}\begin{array}{|c|c|c|c|c|c|}\hline a &\cdots&\frac{-1-\sqrt{3}}{2}&\cdots&\frac{-1+\sqrt{3}}{2}&\cdots\\\hline T’&-&0&+&0&-\\\hdashline T&\searrow&&\nearrow&\text{最大}&\searrow\\\hline\end{array}$

したがって，$T$ は $a=\cfrac{-1+\sqrt{3}}{2}$ で最大値をとる。

・・・ネノハヒ

第2問　問題文

座標平面上で, 放物線 $y=\cfrac{1}{2}x^2+\cfrac{1}{2}$ を $C_1$とし, 放物線 $y=\cfrac{1}{4}x^2$ を $C_2$
とする。

(1) 実数 $a$ に対して, 2直線 $x=a$, $x=a+1$ と $C_1$, $C_2$ で囲まれた図形 $D$ の面積 $S$ は

$\displaystyle S=\int_{a}^{a+1}\Big(\cfrac{1}{\boxed{\text{ア}}}x^2+\cfrac{1}{\boxed{\text{イ}}}\Big)dx$

$=\cfrac{a^2}{\boxed{\text{ウ}}}+\cfrac{a}{\boxed{\text{エ}}}+\cfrac{\boxed{\text{オ}}}{\boxed{\text{カキ}}}$

である。$S$ は $a=\cfrac{\boxed{\text{クケ}}}{\boxed{\text{コ}}}$ で最小値 $\cfrac{\boxed{\text{サシ}}}{\boxed{\text{スセ}}}$ をとる。

(2) 4点 $(a,0)$,$(a+1,0)$,$(a+1,1)$,$(a,1)$ を頂点とする正方形を $R$ で表す。$a$ が $a\geqq0$の範囲を動くとき, 正方形 $R$ と(1)の図形 $D$ の共通部分の面積を $T$ とおく。$T$ が最大となる $a$ の値を求めよう。

直線 $y=1$ は, $C_1$ と $(\pm\boxed{\text{ソ}},1)$ で, $C_2$ と $(\pm\boxed{\text{タ}},1)$ で交わる。したがって, 正方形 $R$ と図形 $D$ の共通部分が空集合にならないのは, $0\leqq a\leqq\boxed{\text{チ}}$ のときである。

$\boxed{\text{ソ}}\leqq a\leqq \boxed{\text{チ}}$ のとき, 正方形 $R$ は放物線 $C_1$ と $x$ 軸の間にあり, この範囲で $a$ が増加するとき, $T$ は $\boxed{\text{ツ}}$。$\boxed{\text{ツ}}$ に当てはまるものを, 次の⓪~②のうちから一つ選べ。

⓪ 増加する　① 減少する ② 変化しない

したがって, $T$ が最大になる $a$ の値は, $0\leqq a\leqq\boxed{\text{ソ}}$ の範囲にある。$0\leqq a\leqq\boxed{\text{ソ}}$ のとき, (1)の図形 $D$ のうち, 正方形 $R$ の外側にある部分の面積 $U$ は

$U=\cfrac{a^3}{\boxed{\text{テ}}}+\cfrac{a^2}{\boxed{\text{ト}}}$

である。よって, $0\leqq a\leqq\boxed{\text{ソ}}$ において

$T=-\cfrac{a^3}{\boxed{\text{ナ}}}-\cfrac{a^2}{\boxed{\text{ニ}}}+\cfrac{a}{\boxed{\text{ヌ}}}+\cfrac{\boxed{\text{オ}}}{\boxed{\text{カキ}}}\cdots\cdots$①

である。①の右辺の増減を調べることにより, $T$ は

$a=\cfrac{\boxed{\text{ネノ}}+\sqrt{\boxed{\text{ハ}}}}{\boxed{\text{ヒ}}}$

で最大値をとることがわかる。