【スマホで読む・わかりやすい】センター数学IIB2016追試【解説・正解・問題】

第4問　解答・解説

アイウ 135　エ 5　オ 4　カ 2　キ 8

ク 5　ケ 1　コ 0　サ 3　シ ス 2 1

セ ソ タ 3 2 2

(1)

三角形の内角の和の公式 $180\degree\times(n-2)$ より

$180\degree\times(8-2)=1080\degree$

$1080\div8=135\degree$

・・・アイウ

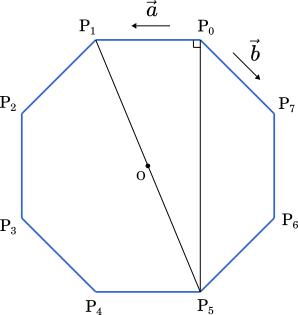
また，図より ∠$\text{P}_1\text{P}_0\text{P}_5=90\degree$

・・・エ

(2)

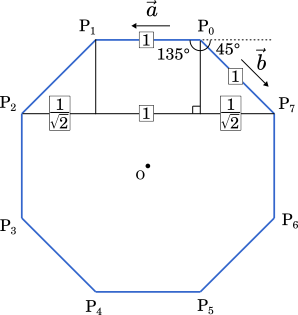
(i) $\overrightarrow{\text{P}_0\text{P}_2}$

$\text{P}_0\text{P}_1:\text{P}_7\text{P}_2=1:\Big(\cfrac{1}{\sqrt{2}}+1+\cfrac{1}{\sqrt{2}}\Big)$

$=1:\Big(1+\cfrac{2}{\sqrt{2}}\Big)$

$=1:(1+\sqrt{2})$

よって

$\overrightarrow{\text{P}_7\text{P}_2}=(1+\sqrt{2})\vec{a}$

$\overrightarrow{\text{P}_0\text{P}_2}=\overrightarrow{\text{P}_0\text{P}_7}+\overrightarrow{\text{P}_7\text{P}_2}$ だから

$\overrightarrow{\text{P}_0\text{P}_2}=(1+\sqrt{2})\vec{a}+\vec{b}$

・・・オ

(ii) $\overrightarrow{\text{P}_0\text{P}_3}$

$\overrightarrow{\text{P}_1\text{P}_2}=\overrightarrow{\text{P}_0\text{P}_2}-\overrightarrow{\text{P}_0\text{P}_1}$

$=(1+\sqrt{2})\vec{a}+\vec{b}-\vec{a}$

$=\sqrt{2}\vec{a}+\vec{b}$

また

$\text{P}_1\text{P}_2:\text{P}_0\text{P}_3=1:(1+\sqrt{2})$ だから

$\overrightarrow{\text{P}_0\text{P}_3}=(1+\sqrt{2})\overrightarrow{\text{P}_1\text{P}_2}$

$=(1+\sqrt{2})(\sqrt{2}\vec{a}+\vec{b})$

$=(2+\sqrt{2})\vec{a}+(1+\sqrt{2})\vec{b}$

・・・カ

(iii) $\overrightarrow{\text{P}_0\text{P}_4}$

$\overrightarrow{\text{P}_0\text{P}_4}=\overrightarrow{\text{P}_0\text{P}_3}+\vec{b}$

$=(2+\sqrt{2})\vec{a}+(1+\sqrt{2})\vec{b}+\vec{b}$

$=(2+\sqrt{2})\vec{a}+(2+\sqrt{2})\vec{b}$

$=(2+\sqrt{2})(\vec{a}+\vec{b})$

・・・キ

(iv) $\overrightarrow{\text{P}_0\text{P}_5}$

$\overrightarrow{\text{P}_0\text{P}_5}=\overrightarrow{\text{P}_0\text{P}_4}+(-\vec{a})$

$=(2+\sqrt{2})\vec{a}+(2+\sqrt{2})\vec{b}-\vec{a}$

$=(1+\sqrt{2})\vec{a}+(2+\sqrt{2})\vec{b}$

・・・ク

(v) $\overrightarrow{\text{P}_0\text{P}_6}$

$\overrightarrow{\text{P}_0\text{P}_6}=\overrightarrow{\text{P}_0\text{P}_5}+(-\overrightarrow{\text{P}_1\text{P}_2})$

$=(1+\sqrt{2})\vec{a}+(2+\sqrt{2})\vec{b}-\sqrt{2}\vec{a}-\vec{b}$

$=\vec{a}+(1+\sqrt{2})\vec{b}$

・・・ケ

(3)

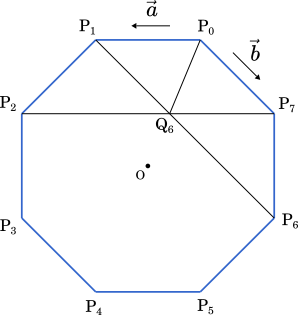
$\text{Q}_6$ は $\text{P}_6\text{P}_9$ と $\text{P}_7\text{P}_{10}$ の交点であり，言い換えると $\text{P}_6\text{P}_1$ と $\text{P}_7\text{P}_2$ の交点である。

したがって，$\overrightarrow{\text{P}_0\text{Q}_6}=\vec{a}+\vec{b}$

・・・コ

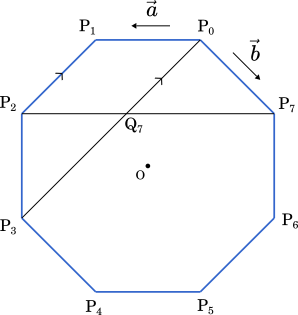
$\text{Q}_7$ は $\text{P}_7\text{P}_{10}$ と $\text{P}_8\text{P}_{11}$ の交点で，言い換えると $\text{P}_7\text{P}_2$ と $\text{P}_0\text{P}_3$ の交点である。

したがって，$\overrightarrow{\text{P}_0\text{Q}_7}=\overrightarrow{\text{P}_1\text{P}_2}=\sqrt{2}\vec{a}+\vec{b}$

・・・サ

(4)

$\overrightarrow{\text{Q}_6\text{Q}_7}=\overrightarrow{\text{P}_0\text{Q}_7}-\overrightarrow{\text{P}_0\text{Q}_6}$

$=\sqrt{2}\vec{a}+\vec{b}-\vec{a}-\vec{b}=(\sqrt{2}-1)\vec{a}$

$\text{P}_0\text{Q}_7$ と $\text{P}_1\text{Q}_6$ の交点を R とすると，△$\text{RP}_0\text{P}_1$ ∽ △$\text{RQ}_6\text{Q}_7$ が成り立つ。よって

$\text{P}_0\text{P}_1:\text{Q}_6\text{Q}_7=1:(\sqrt{2}-1)$

・・・シス

よって，面積の比は

$1^2:(\sqrt{2}-1)^2$

$(\sqrt{2}-1)^2=2-2\sqrt{2}+1=3-2\sqrt{2}$

したがって，$3-2\sqrt{2}$ 倍

・・・セソタ

[ad]

第4問　問題文

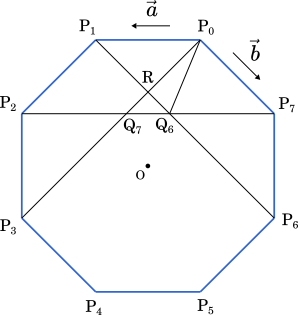
正八角形 $\text{P}_0\text{P}_1\text{P}_2\text{P}_3\text{P}_4\text{P}_5\text{P}_6\text{P}_7$ を考える。$\overrightarrow{\text{P}_0\text{P}_1}=\vec{a}$, $\overrightarrow{\text{P}_0\text{P}_7}=\vec{b}$ とおく。

(1) 正八角形の一つの内角は $\boxed{\text{アイウ}}\degree$ である。また, $\angle\text{P}_1\text{P}_0\text{P}_{\boxed{\text{エ}}}=90\degree$ である。

以下の, (2)の $\boxed{\text{オ}}$~$\boxed{\text{ケ}}$, および(3)の $\boxed{\text{コ}}$, $\boxed{\text{サ}}$ については, 当てはまるものを, 次の⓪~⑨のうちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。

⓪ $\vec{a}+\vec{b}$　① $\vec{a}+(1+\sqrt{2})\vec{b}$

② $(2+\sqrt{2})\vec{a}+(1+\sqrt{2})\vec{b}$

③ $\sqrt{2}\vec{a}+\vec{b}$　④　$(1+\sqrt{2})\vec{a}+\vec{b}$

⑤ $(1+\sqrt{2})\vec{a}+(2+\sqrt{2})\vec{b}$

⑥ $\vec{a}+\sqrt{2}\vec{b}$　⑦ $(1+\sqrt{2})(\vec{a}+\vec{b})$

⑧ $(2+\sqrt{2})(\vec{a}+\vec{b})$　⑨ $\sqrt{2}(\vec{a}+\vec{b})$

(2) $k=1,2,\cdots,7$ に対して, ベクトル $\overrightarrow{\text{P}_0\text{P}_k}$ を $\vec{a},\vec{b}$ を用いて表すと

$\overrightarrow{\text{P}_0\text{P}_1}=\vec{a}$, $\overrightarrow{\text{P}_0\text{P}_2}=\boxed{\text{オ}}$, $\overrightarrow{\text{P}_0\text{P}_3}=\boxed{\text{カ}}$, $\overrightarrow{\text{P}_0\text{P}_4}=\boxed{\text{キ}}$, $\overrightarrow{\text{P}_0\text{P}_5}=\boxed{\text{ク}}$, $\overrightarrow{\text{P}_0\text{P}_6}=\boxed{\text{ケ}}$,$\overrightarrow{\text{P}_0\text{P}_7}=\vec{b}$

である。

(3) $k=0,1,\cdots,7$ に対して, 対角線 $\text{P}_k\text{P}_{k+3}$ と対角線 $\text{P}_{k+1}\text{P}_{k+4}$ の交点を $\text{Q}_k$ とする。ただし, $\text{P}_8$, $\text{P}_9$, $\text{P}_{10}$, $\text{P}_{11}$ は,それぞれ $\text{P}_0$, $\text{P}_1$, $\text{P}_2$, $\text{P}_3$ を表すものとする。

このとき, $\overrightarrow{\text{P}_0\text{Q}_6}=\boxed{\text{コ}}$, $\overrightarrow{\text{P}_0\text{Q}_7}=\boxed{\text{サ}}$ である。

(4) $\overrightarrow{\text{Q}_6\text{Q}_7}=(\sqrt{\boxed{\text{シ}}-\boxed{\text{ス}}})\vec{a}$ ある。したがって, 正八角形 $\text{Q}_0\text{Q}_1\text{Q}_2\text{Q}_3\text{Q}_4\text{Q}_5\text{Q}_6\text{Q}_7$ の面積は, 正八角形 $\text{P}_0\text{P}_1\text{P}_2\text{P}_3\text{P}_4\text{P}_5\text{P}_6\text{P}_7$ の面積の $(\boxed{\text{セ}}-\boxed{\text{ソ}}\sqrt{\boxed{\text{タ}}})$ 倍である。