【スマホで読む・わかりやすい】共通テスト数学IIB2021第2日程【解説・正解・問題】

第4問　正解
ア　4　イ,ウ　4,5　エ,オカ　5,16
キ　5　ク　4　ケ,コ　1,1　サシ　15
ス,セ　1,2　ソタ　41　チツテ　153

〔1〕

$S_n=5^n-1$ とすると

$a_1=S_1$
$=5^1-1=4$

・・・ア

また，$n\geqq2$ のとき

$S_n-S_{n-1}=a_n$ より

$a_n=5^n-1-(5^{n-1}-1)$
$=5^n-5^{n-1}$
$=5\cdot5^{n-1}-5^{n-1}$
$=(5-1)\cdot5^{n-1}$
$=4\cdot5^{n-1}$

・・・イ，ウ

また

$\cfrac{1}{a_n}=\cfrac{1}{4\cdot5^{n-1}}$
$=\cfrac{1}{4}\cdot\Big(\cfrac{1}{5}\Big)^{n-1}$

よって，$\cfrac{1}{a_n}$ は，初項 $\cfrac{1}{4}$，公比 $\cfrac{1}{5}$ の等比数列である。

$\displaystyle\sum_{k=1}^n\cfrac{1}{a_k}$

これは，等比数列 $\Big\{\cfrac{1}{a_k}\Big\}$ の和だから，公式 $\cfrac{a(1-r^n)}{1-r}$ を用いて

$=\cfrac{\cfrac{1}{4}\Big\{1-\Big(\cfrac{1}{5}\Big)^n\Big\}}{1-\cfrac{1}{5}}$
$=\cfrac{\cfrac{1}{4}(1-5^{-n})}{\cfrac{4}{5}}$
$=\cfrac{\cfrac{1}{4}(1-5^{-n})\times20}{\cfrac{4}{5}\times20}$
$=\cfrac{5}{16}(1-5^{-n})$

・・・エ，オカ，キ

〔2〕(1)

$n=1$ のとき $3n+1=3\cdot1+1=4$ だから，4 枚のタイルの配置を考えると

$t_1=4$ (通り)

・・・ク

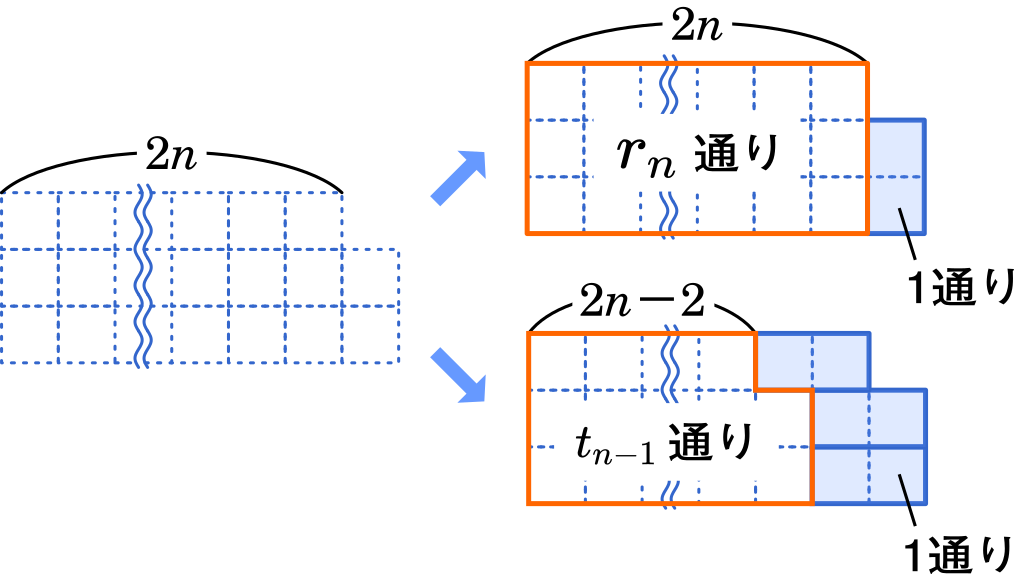
右下隅のタイルを縦向きに置いた場合，置き方は 1 通りだから，全体で $r_n\times1$ 通り。

右下隅のタイルを横向きに置いた場合も，$t_{n-1}$ を除いた部分の置き方は 1 通りしかない。よって，全体で $t_{n-1}\times1$ 通り。

よって，$n\geqq2$ のとき

$t_n=r_n+t_{n-1}$

したがって，$A=1$，$B=1$ である。

・・ケ，コ

また

$t_2=r_2+t_1=11+4=15$

・・・サシ

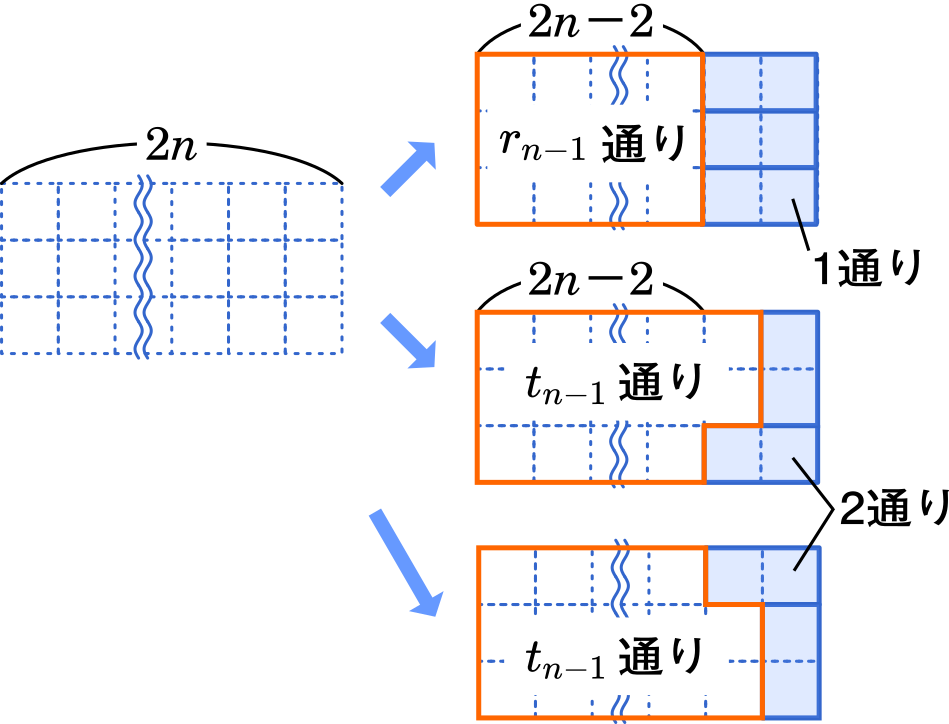
右下隅のタイルを横向きに置いた場合，その上にさらに横向きのタイルを 2 枚置く方法がある。この場合，全体で $r_{n-1}\times1$ 通り。

また，右下隅のタイルを横向きに置き，その上にタイルを縦向きに置くこともできる。この場合，全体で $t_{n-1}\times1$ 通り。

さらに，右下隅のタイルを横向きに置き，その上にタイルを横向きに置く。この場合，全体で $t_{n-1}\times2$ 通り。

よって

$r_n=r_{n-1}+2t_{n-1}$

したがって，$C=1$，$D=2$ である。

・・・ス，セ

〔2〕(2)

$2n=6$ より $n=3$ とすると

$r_3=r_2+2t_2$
$=11+2\cdot15=41$

・・・ソタ

また，$2n=8$ より $n=4$ とすると

$r_4=r_3+2t_3$
$=41+2t_3$

ここで

$t_3=r_3+t_2=41+15=56$

したがって

$r_4=41+2\cdot56$
$=153$

・・・チツテ

問題文

第3問～第5問は，いずれか2問を選択し，解答しなさい。

第4問　(選択問題)

〔1〕 自然数 $n$ に対して，$S_n=5^n-1$ とする。さらに，数列 $\{a_n\}$ の初項から第 $n$ 項までの和が $S_n$ であるとする。このとき，$a_1=\boxed{\sf{ア}}$ である。また，$n\geqq 2$ のとき

$a_n=\boxed{\sf{イ}}\cdot\boxed{\sf{ウ}}^{n-1}$

である。この式は $n=1$ のときにも成り立つ。

上で求めたことから，すべての自然数 $n$ に対して

$\displaystyle\sum_{k=1}^n\cfrac{1}{a_k}=\cfrac{\boxed{\sf{エ}}}{\boxed{\sf{オカ}}}(1-\boxed{\sf{キ}}^{-n})$

が成り立つことがわかる。 

〔2〕 太郎さんは和室の畳を見て，畳の敷き方が何通りあるかに興味を持った。ちょうど手元にタイルがあったので，畳をタイルに置き換えて，数学的に考えることにした。

縦の長さが 1，横の長さが 2 の長方形のタイルが多数ある。それらを縦か横の向きに，隙間も重なりもなく敷き詰めるとき，その敷き詰め方をタイルの「配置」と呼ぶ。

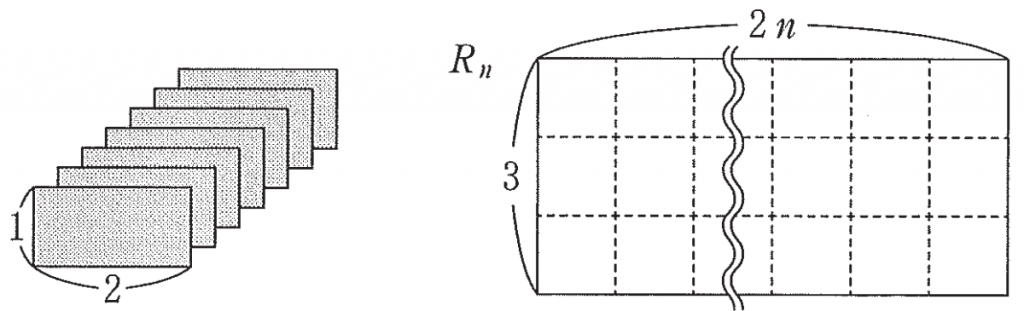
上の図のように，縦の長さが 3，横の長さが $2n$ の長方形を $R_n$ とする。$3n$ 枚のタイルを用いた $R_n$ 内の配置の総数を $r_n$ とする。

$n=1$ のときは，下の図のように $r_1=3$ である。

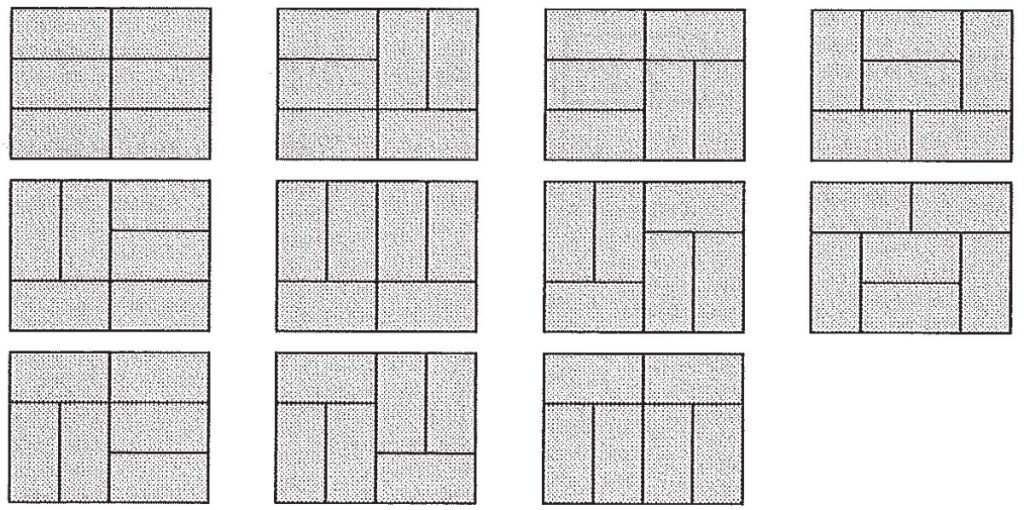
また，$n=2$ のときは，下の図のように $r_2=11$ である。

(1) 太郎さんは次のような図形 $T_n$ 内の配置を考えた。

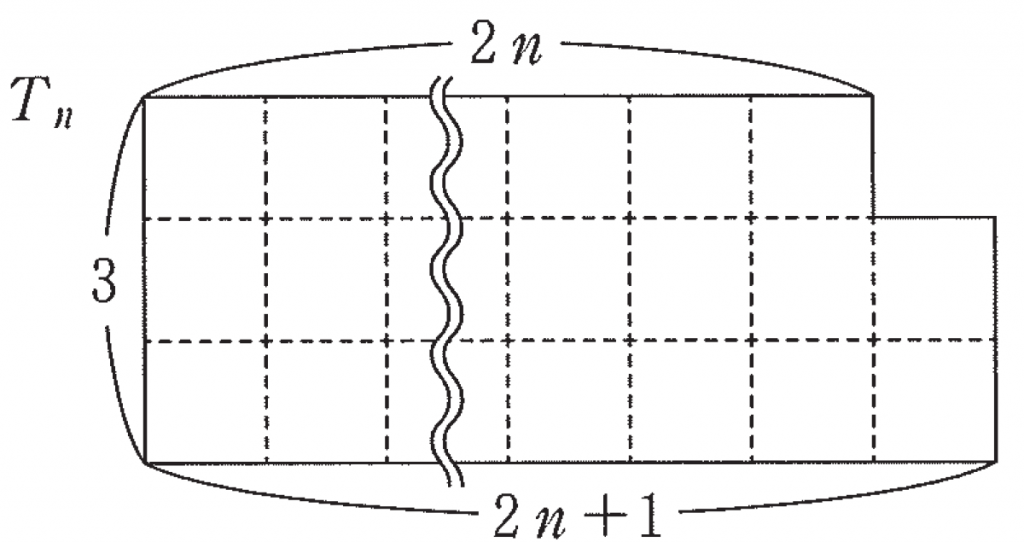
$(3n+1)$ 枚のタイルを用いた $T_n$ 内の配置の総数を $t_n$ とする。$n=1$ のときは，$t_1=\boxed{\sf{ク}}$ である。

さらに，太郎さんは $T_n$ 内の配置について，右下隅のタイルに注目して次のような図をかいて考えた。

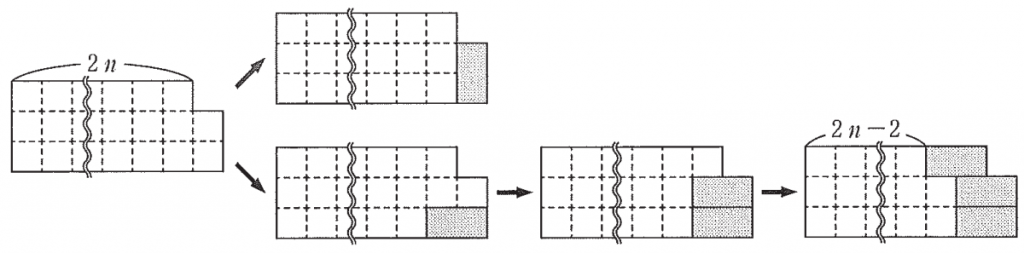
この図から，2 以上の自然数 $n$ に対して

$t_n=Ar_n+Bt_{n-1}$

が成り立つことがわかる。ただし，$A=\boxed{\sf{ケ}}$，$B=\boxed{\sf{コ}}$ である。
以上から，$t_2=\boxed{\sf{サシ}}$ であることがわかる。

同様に，$R_2$ の右下隅のタイルに注目して次のような図をかいて考えた。

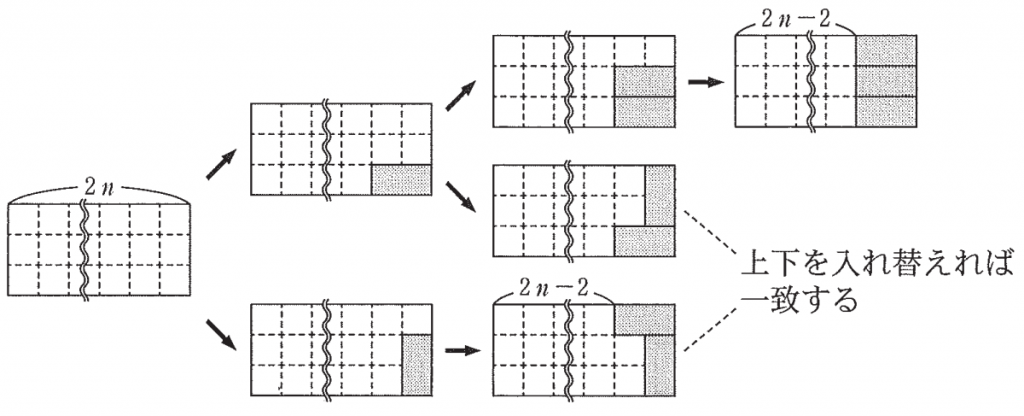
この図から，2 以上の自然数 $n$ に対して

$r_n=Cr_{n-1}+Dt_{n-1}$

が成り立つことがわかる。ただし，$C=\boxed{\sf{ス}}$，$D=\boxed{\sf{セ}}$ である。

(2) 畳を縦の長さが 1，横の長さが 2 の長方形とみなす。縦の長さが 3，横の長さが 6 の長方形の部屋に畳を敷き詰めるとき，敷き詰め方の総数は $\boxed{\sf{ソタ}}$ である。

また，縦の長さが 3，横の長さが 8 の長方形の部屋に畳を敷き詰めるとき，敷き詰め方の総数は $\boxed{\sf{チツテ}}$ である。