【スマホで読む・わかりやすい】共通テスト試行H30年度数学IA【解説・正解・問題】
第4問
ある物体 X の質量を天秤ばかりと分銅を用いて量りたい。天秤ばかりは支点の両側に皿 A,B が取り付けられており,両側の皿にのせたものの質量が等しいときに釣り合うように作られている。分銅は 3g のものと 8g のものを何個でも使うことができ,天秤ばかりの皿の上には分銅を何個でものせることができるものとする。以下では,物体 X の質量を $M$(g)とし,$M$ は自然数であるとする。
(1)
天秤ばかりの A に物体 X をのせ,皿 B に 3g の分銅 3 個をのせたところ,天秤ばかりは B の側に傾いた。さらに,皿 A に 8g の分銅 1 個をのせたところ,天秤ばかりは A の側に傾き,皿 B に 3g の分銅 2 個をのせると天秤ばかりは釣り合った。このとき,A,B にのせているものの質量を比較すると
$M+8\times\boxed{\text{ ア }}=3\times\boxed{\text{ イ }}$
が成り立ち,$M=\boxed{\text{ ウ }}$である。上の式は
$3\times\boxed{\text{ イ }}+8\times(-\boxed{\text{ ア }}) = M$ と変形することができ,$x=\boxed{\text{ イ }}$,$y=-\boxed{\text{ ア }}$ は,方程式 $3x + 8y = M$ の整数解の一つである。
正解と解説
ア,イ,ウ 1,5,7
問題文にしたがって物体 X と分銅を置くと,以下のようになる。
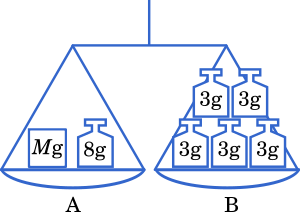
左右でつり合っているので
$M+8\times1=3\times5$
式を解いて,$M=7$
(2)
$M = 1$のとき,皿 A に物体 X と 8g の分銅 $\boxed{\text{ エ }}$ 個をのせ,皿 B に 3g の分銅 3 個をのせると釣り合う。
よって,$M$ がどのような自然数であっても,皿 A に物体 X と 8g の分銅 $\boxed{\text{ オ }}$ 個をのせ,皿 B に3g の分銅 $\boxed{\text{ カ }}$ 個をのせることで釣り合うことになる。$\boxed{\text{ オ }}$,$\boxed{\text{ カ }}$ に当てはまるものを,次の⓪~⑤ のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ $M-1$ ① $M$ ② $M+1$
③ $M+3$ ④ $3M$ ⑤ $5M$
解答・解説
エ,オ,カ 1,1,4
$M=1$ のとき,8g の分銅を $k$ 個とすると
$1+8\times k=3\times 3$
$k=1$
上の式は $k=1$ を代入して
$1+8\times 1=3\times 3$ となる。
両辺を $M$ 倍すると
$M+8M=3\times 3M$
よって,$M$ がどのような自然数であっても,皿 A に物体 X と 8g の分銅 $M$ 個をのせ,皿 B に3g の分銅 $3M$ 個をのせることで釣り合うことになる。
(3)
$M = 20$ のとき,皿 A に物体 X と 3g の分銅 $p$ 個を,皿 B に 8g の分銅 $q$ 個をのせたところ,天秤ばかりが釣り合ったとする。このような自然数の組 $(p,q)$ のうちで,$p$ の値が最小であるものは $p=\boxed{\text{ キ }}$,$q=\boxed{\text{ ク }}$ であり,方程式 $3x + 8y = 20$ のすべての整数解は,整数 $n$ を用いて
$x = \boxed{\text{ ケコ }}+\boxed{\text{ サ }}n$,$y=\boxed{\text{ ク }}-\boxed{\text{ シ }}n$
と表すことができる。
正解と解説
キ,ク 4,4 ケコ,サ,シ -4,8,3
問題文より式を作ると
$20+3p=8q$
$-3p+8q=20$
恒等式が成り立つように $p,q$ にさまざまな値を代入する。そうすると,$p=4$,$q=4$ のときに左辺が
$-3\times 4+8\times 4=20$
となり,恒等式が成り立つ。
次に,方程式 $3x+8y=20$ のすべての整数解を求める。上で求めた $-3\times 4+8\times 4=20$ を利用するとよい。
$3x+8y=20\cdots$①
$3(-4)+8\cdot 4=20\cdots$②
①-②
$3(x+4)+8(y-4)=0$
$3(x+4)=-8(y-4)$
$3$ と $8$ は互いに素であるから
$x+4$ は $8$ の倍数である。整数 $n$ を用いて
$x+4=8n$
$x=-4+8n$
これを①に代入して
$3(8n-4)+8y=20$
$y=4-3n$
(4)
$M = \boxed{\text{ ウ }}$とする。3g と 8g の分銅を,他の質量の分銅の組み合わせに変えると,分銅をどのようにのせても天秤ばかりが釣り合わない場合がある。この場合の分銅の質量の組み合わせを,次の⓪~③のうちからすべて選べ。ただし,2 種類の分銅は,皿 A,皿 B のいずれにも何個でものせることができるものとする。 $\boxed{\text{ ス }}$
⓪ 3g と 14g ① 3g と 21g
② 8g と 14g ③ 8g と 21g
正解と解説
ス 1,2
問題文より,$M=7$ のときに条件を満たす整数 $x,y$ が存在しないものを選ぶ。
(i) 3g と 14g の場合
$3x+14y=7$
右辺を 1 とした式をつくると
$3x+14y=1$
$(x,y)=(5,-1)$ のとき,恒等式は成り立つ。
$3\times 5+14(-1)=1$
両辺を 7 倍すると
$3\times 35+14(-7)=7$
となり,条件を満たす整数 $x,y$ が存在する。よって,⓪は不適。
(ii) 3g と 21g
$3x+21y=7$
$3(x+7y)=7$
左辺は 3 の倍数だから 7 になることはない。よって条件を満たす整数 $x,y$ は存在しないので,①は適する。
(iii) 8g と 14g
$8x+14y=7$
$2(4x+7y)=7$
左辺は 2 の倍数だから 7 になることはない。よって条件を満たす整数 $x,y$ は存在しないので,②は適する。
(iv) 8g と 21g
$8x+21y=7$
$8x+21y=1$ とおいて,式を満たす整数 $x,y$ を考える。
互除法を用いなくても,8 の倍数と 21 の倍数を並べていけば差が 1 になる組み合わせは容易に見つけられる。
$8\cdot 8+21(-3)=1$
となり,条件を満たす整数 $x,y$ が存在する。よって,③は不適。
(5)
皿 A には物体 X のみをのせ,3g と 8g の分銅は皿 B にしかのせられないとすると,天秤ばかりを釣り合わせることでは $M$ の値を量ることができない場合がある。このような自然数 $M$ の値は,$\boxed{\text{ セ }}$ 通りあり,そのうち最も大きい値は $\boxed{\text{ ソタ }}$ である。
ここで,$M$ > $\boxed{\text{ ソタ }}$ であれば,天秤ばかりを釣り合わせることで $M$ の値を量ることができる理由を考えてみよう。$x$ を 0 以上の整数とするとき,
(i) $3x + 8\times0$ は 0 以上であって,3 の倍数である。
(ii) $3x + 8\times 1$ は 8 以上であって,3 で割ると 2 余る整数である。
(iii) $3x + 8\times 2$ は 16 以上であって,3 で割ると 1 余る整数である。
$\boxed{\text{ ソタ }}$ より大きな $M$ の値は(i),(ii),(iii)のいずれかに当てはまることから,0 以上の整数 $x, y$ を用いて $M = 3x + 8y$ と表すことができ,3g の分銅 $x$ 個と 8g の分銅 $y$ 個を皿 B にのせることで $M$ の値を量ることができる。
このような考え方で,0 以上の整数 $x, y$ を用いて $3x + 2018y$ と表すことができないような自然数の最大値を求めると,$\boxed{\text{ チツテト }}$ である。
正解と解説
セ,ソタ,チツテト 7,13,4033
先に $\boxed{\text{ ソタ }}$ から考えるとよい。
$k$ を整数とすると (i),(ii),(iii) は $3k,3k+2,3k+1$ と表すことができ,すべての整数を表す。
ただし,(ii) 8 以上と (iii) 16 以上という条件から,実際にはすべての整数ではない。(ii),(iii)の条件から少なくとも 16 以上の数はすべて表すことができるので,1 から 15 について考えると
$3k=3,6,9,12,15$
$3k+2=8,11,14$ (8 以上の場合)
$3k+1$ は 16 以上だから 1~15 の範囲にはない
1 から 15 の間で,いずれにも当てはまらない数は $1,2,4,5,7,10,13$ の $7$ 通りである。そのうちもっとも大きな値は $13$ である。
次に $3x+2018y$ について考える。
上と同様にして
(i) $3x+2018\times 0$ は 0 以上であって,3 の倍数である。
(ii) $3x+2018\times 1$ は 2018 以上であって,3 で割ると 2 余る整数である。
(iii) $3x+2018\times 2$ は 4036 以上であって,3 で割ると 1 余る整数である。
(i),(ii),(iii) を $3k,3k+1,3k+2$ とすると,少なくとも 4036 以上の数はすべて表すことができる。
求める最大値が 4036 付近にあると考えて
4036 は 3 で割ると 1 余るので
4035 は 3 で割りきれる
4034 は 3 で割ると 2 余る
4033 は 3 で割ると 1 余る
4034までは(i)~(iii)のいずれかの条件を満たすが,4033 は条件(ii)に反する。よって,最大値は $4033$ である。
SNSでシェア