【スマホで読む・わかりやすい】共通テスト数学IA2021第2日程【解説・正解・問題】

第5問　正解

ア　5　イ,ウ,エ　2,6,7　オ　1
カ　2　キ　2　ク,ケコ　2,15
サシ　15　ス,セソ　3,15
タ,チ　4,5　ツ,テ　5,3

(1)

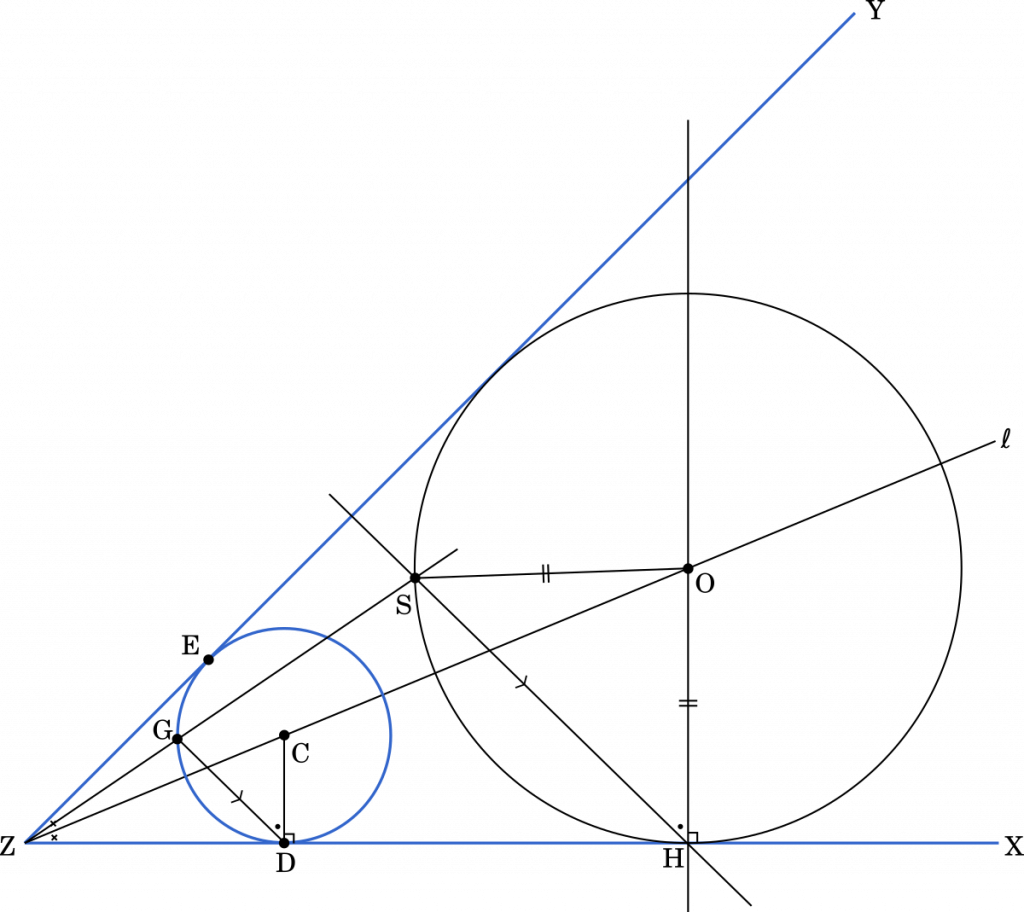
上の図より，OH と OS はともに円 O の半径だから，円 O が点 S を通り，半直線 ZX と半直線 ZY の両方に接する円であることを示すには，OH ＝ OS が成り立つことを示せばよい。

・・・ア

DG // HS　より △ZDG ∽ △ZHS だから

DG : HS ＝ ZD : ZH

・・・イ，ウ，エ

また，DC // HO より △ZDC ∽ △ZHO だから

DC : HO ＝ ZD : ZH

・・・オ

よって，DG : HS ＝ DC : HO となる。

ここで，3 点 S，O，H が一直線上にない場合には，∠CDG ＝ ∠OHS であるので，△CDG と △OHS との関係に着目すると，CD ＝ CG より OH = OS であることが分かる。

・・・カ

なお，3点 S，O，H が一直線上にある場合，HS は半直線 ZX の垂線となるので，それと平行な DG も，半直線 ZX の垂線となる。

点 G は円 C 上の点だから，DG は円の直径である。したがって，DG ＝ 2DC となり，DG : HS ＝ DC : HO より OH ＝ OS であることがわかる。

・・・キ

(2)

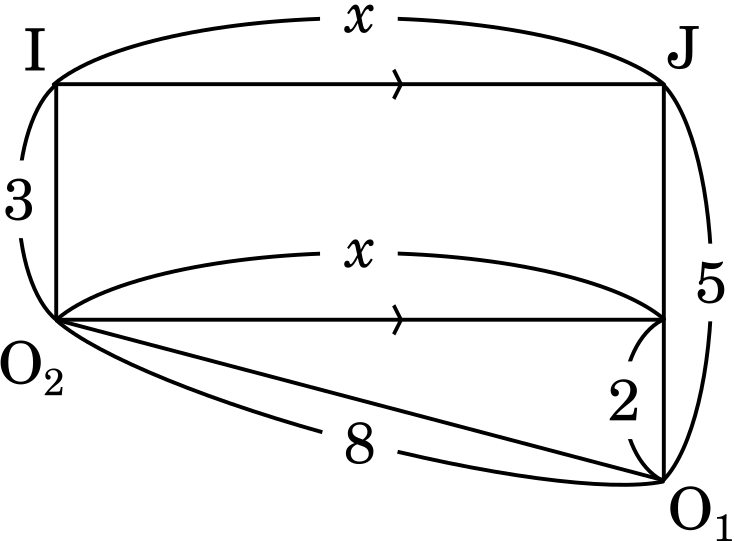
IJ ＝ $x$ とすると，三平方の定理より

$x^2+2^2=8^2$
$x^2=64-4=60$
$x=\sqrt{60}=2\sqrt{15}$

したがって

IJ ＝ $2\sqrt{15}$

・・・ク，ケコ

方べきの定理より

LM・LK ＝ $\text{LS}^2$

ここで，LS の長さを求めると

$\triangle\text{ZIO}_2$ ∽ $\triangle\text{ZJO}_1$

また，$\text{O}_1\text{O}_2=5+3=8$ だから

$\text{ZO}_2:\text{ZO}_2+8=3:5$
$5\text{ZO}_2=3(\text{ZO}_2+8)$
$5\text{ZO}_2=3\text{ZO}_2+24$
$2\text{ZO}_2=24$
$\text{ZO}_2=12$

また

$\text{ZI}:\text{ZI}+2\sqrt{15}=3:5$
$5\text{ZI}=3(\text{ZI}+2\sqrt{15})$
$5\text{ZI}=3\text{ZI}+6\sqrt{15}$
$2\text{ZI}=6\sqrt{15}$
$\text{ZI}=3\sqrt{15}$

・・・ス，セソ

よって，$\triangle\text{ZIO}_2$ は辺の長さが $\text{ZI}=3\sqrt{15}$，$\text{IO}_2=3$，$\text{ZO}_2=12$ の三角形であることが分かる。

これを用いて，他の相似の関係にある三角形の辺の長さを求ると良い。

ここで，求めたいものは LS であったことを踏まえて

$\triangle\text{ZIO}_2$ ∽ $\triangle\text{ZSL}$ より

$\text{ZI}:3=\text{ZS}:\text{LS}$
$\text{ZI}:3=\text{ZO}_2+3:\text{LS}$
$3\sqrt{15}:3=12+3:\text{LS}$
$3\sqrt{15}:3=15:\text{LS}$
$3\sqrt{15}:3=15:\text{LS}$
$3\sqrt{15}\cdot\text{LS}=3\times15$
$\sqrt{15}\cdot\text{LS}=15$
$\text{LS}=\cfrac{15}{\sqrt{15}}$
$=\cfrac{15\sqrt{15}}{15}$
$=\sqrt{15}$

したがって

$\text{LS}^2=15$

・・・サシ

また，直線 LK と直線 $\ell$ との交点を N とし，直線 LS と半直線 ZX の交点を T とすると
$\triangle\text{ZIO}_2$ ∽ $\triangle\text{ZKO}_1$ より

$\text{ZI}:\text{ZK}=3:5$
$\text{ZK}=\cfrac{5}{3}\times\text{ZI}$
$=\cfrac{5}{3}\times3\sqrt{15}=5\sqrt{15}$

また，$\triangle\text{ZIO}_2$ ∽ $\triangle\text{ZST}$ より

$\text{ZO}_2:\text{ZT}=3:\text{ST}$

ST ＝ LS より

$12:\text{ZT}=3:\sqrt{15}$
$\text{ZT}=\cfrac{12\sqrt{15}}{3}=4\sqrt{15}$

メネラウスの定理より

$\cfrac{\text{LN}}{\text{NK}}\times\cfrac{5\sqrt{15}}{4\sqrt{15}}\times\cfrac{1}{1}=1$
$\cfrac{\text{LN}}{\text{NK}}=\cfrac{4}{5}$

・・・タチ

よって，LN : NK = 4 :5 である。

さらに，メネラウスの定理を用いて

TK ＝ $5\sqrt{15}-4\sqrt{15}=\sqrt{15}$ より

$\cfrac{4\sqrt{15}}{\sqrt{15}}\times\cfrac{9}{4}\times\cfrac{\text{NS}}{\text{SZ}}=1$
$\cfrac{\text{NS}}{\text{SZ}}=\cfrac{1}{9}$
$\text{SN}=\cfrac{1}{9}\times\text{SZ}$
$\text{SN}=\cfrac{1}{9}(\text{ZO}_2+3)$
$=\cfrac{1}{9}\times15$
$=\cfrac{5}{3}$

・・・ツテ

問題文

第3問～第5問は，いずれか2問を選択し，解答しなさい。 

第5問 (選択問題)

点 Z を端点とする半直線 ZX と半直線 ZY があり，0° < ∠XZY < 90° とする。また，0° < ∠SZX < ∠XZY かつ 0° < ∠SZY < ∠XZY を満たす点 S をとる。点 S を通り，半直線 ZX と半直線 ZY の両方に接する円を作図したい。

円 O を，次の(Step 1)～(Step 5)の手順で作図する。

手順

(Step 1) ∠XZY の二等分線 $\ell$ 上に点 C をとり，下図のように半直線 ZX と半直線 ZY の両方に接する円 C を作図する。また，円 C と半直線 ZX との接点を D，半直線 ZY との接点を E とする。
(Step 2) 円 C と直線 ZS との交点の一つを G とする。
(Step 3) 半直線 ZX 上に点 H を DG//HS を満たすようにとる。
(Step 4) 点 H を通り，半直線 ZX に垂直な直線を引き，$\ell$ との交点を O とする。
(Step 5) 点 O を中心とする半径 OH の円 O をかく。 

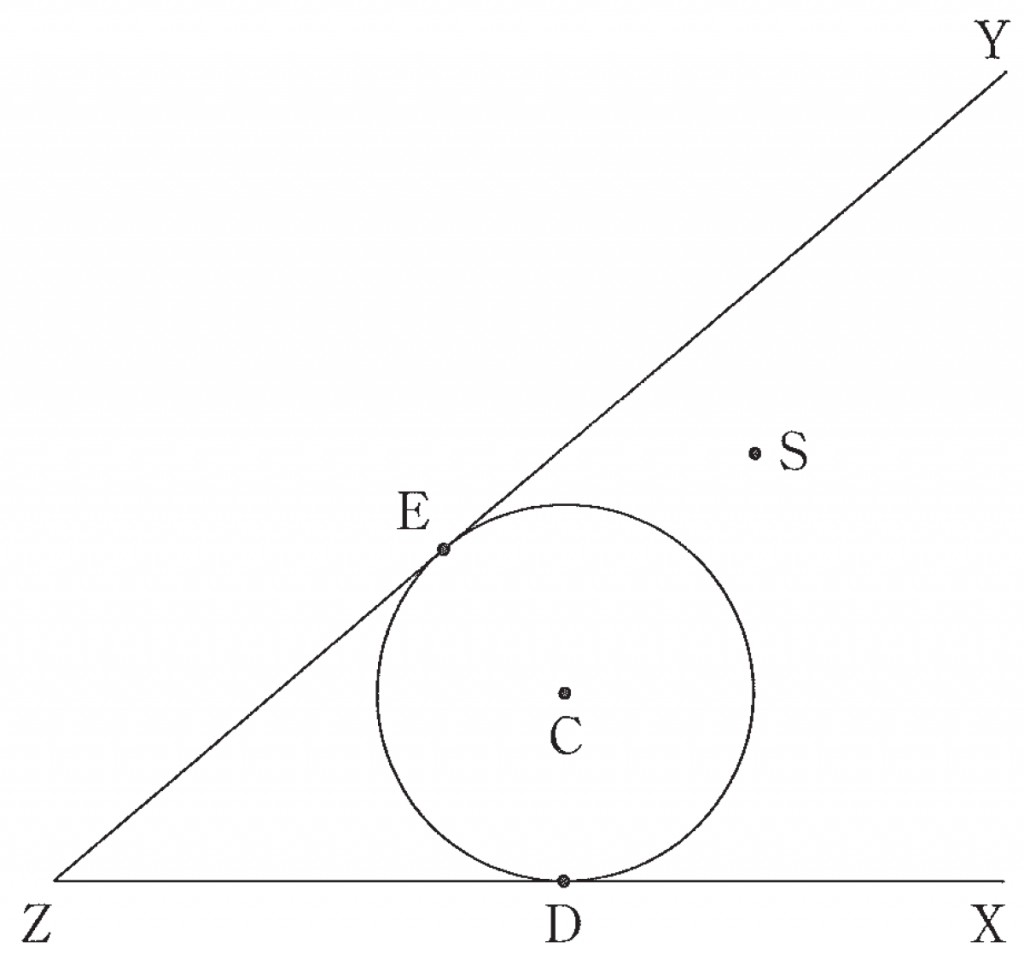
参考図 

(1) (Step 1)～(Step 5)の手順で作図した円 O が求める円であることは，次の構想に基づいて下のように説明できる。

構想 

円 O が点 S を通り，半直線 ZX と半直線 ZY の両方に接する円であることを示すには，OH = $\boxed{\boxed{\sf{ア}}}$が成り立つことを示せばよい。

作図の手順より，△ZDG と △ZHS との関係，および △ZDC と △ZHO との 関係に着目すると

DG：$\boxed{\boxed{\sf{イ}}}$ = $\boxed{\boxed{\sf{ウ}}}$：$\boxed{\boxed{\sf{エ}}}$
DC：$\boxed{\boxed{\sf{オ}}}$ = $\boxed{\boxed{\text{ウ}}}$：$\boxed{\boxed{\text{エ}}}$

であるから，DG：$\boxed{\boxed{\text{イ}}}$ = DC：$\boxed{\boxed{\text{オ}}}$となる。

ここで，3 点 S，O，H が一直線上にない場合は，∠CDG = ∠$\boxed{\boxed{\sf{カ}}}$ であるので，△CDG と △$\boxed{\boxed{\text{カ}}}$ との関係に着目すると，CD = CG より OH = $\boxed{\boxed{\text{ア}}}$ であることがわかる。

なお，3 点 S，O，H が一直線上にある場合は，DG = $\boxed{\sf{キ}}$ DC となり，DG：$\boxed{\boxed{\text{イ}}}$ = DC：$\boxed{\boxed{\text{オ}}}$ より OH = $\boxed{\boxed{\text{ア}}}$ であることがわかる。

$\boxed{\boxed{\text{ア}}}$～$\boxed{\boxed{\text{オ}}}$ の解答群(同じものを繰り返し選んでもよい。) 

⓪ DH　① HO　② HS
③ OD　④ OG　⑤ OS
⑥ ZD　⑦ ZH　⑧ ZO
⑨ ZS

$\boxed{\boxed{\text{カ}}}$ の解答群

⓪ OHD　① OHG　② OHS
③ ZDS　④ ZHG　⑤ ZHS
⑥ ZOS　⑦ ZCG

(2) 点 S を通り，半直線 ZX と半直線 ZX の両方に接する円は二つ作図できる。特に，点 S が ∠XZY の二等分線 $\ell$ 上にある場合を考える。半径が大きい方の円の中心を $\text{O}_1$ とし，半径が小さい方の円の中心を $\text{O}_2$ とする。また，円 $\text{O}_2$ と半直線 ZX が接する点を I とする。円 $\text{O}_1$ と半直線 ZY が接する点を J とし，円 $\text{O}_1$ と半直線 ZX が接する点を K とする。

作図をした結果，円 $\text{O}_1$ の半径は 5，円 $\text{O}_2$ の半径は 3 であったとする。このとき，IJ = $\boxed{\sf{ク}}\sqrt{\boxed{\sf{ケコ}}}$ である。さらに，円 $\text{O}_1$ と円 $\text{O}_2$ の接点 S における共通接線と半直線 ZY との交点を L とし，直線 LK と円 $\text{O}_1$ との交点で点 K とは異なる点を M とすると

LM・LK = $\boxed{\sf{サシ}}$

である。

また，ZI = $\boxed{\sf{ス}}\sqrt{\boxed{\sf{セソ}}}$ であるので，直線 LK と直線 $\ell$ との交点を N とすると

$\cfrac{\text{LN}}{\text{NK}}=\cfrac{\boxed{\sf{タ}}}{\boxed{\sf{チ}}}$，$\text{SN}=\cfrac{\boxed{\sf{ツ}}}{\boxed{\sf{テ}}}$

である。